心中有丘壑，筆下生云煙
——以對稱視角下的錯解分析為例

☉山東省臨清市京華中學 齊 欣

參考文獻［1］指出體會對稱之美，欣賞對稱之妙，是貫穿在整個學習過程中的.參考文獻［2］指出，對稱是一種審美心向下的思維走勢，是一種方向性引領，引領我們走出困境，走向澄明.筆者深受啟發，結合教學實踐及閱讀參考文獻［3］的思考，基于兩個案例，分析解題過程中的錯因，注重學生對其中蘊含的數學本質的理解，才能讓學生領悟解題的真諦，達到“吃一塹，長一智”的目的，還要引導學生體會解題糾錯中滲透的方法、蘊含的哲理.

一、糾錯案例展示

案例1：（2016年成都卷第24題）實數a、n、m、b滿足a＜n＜m＜b，這四個數在數軸上對應的點分別是A、N、M、B（如圖1），若AM2=BM·AB，BN2=AN·AB，則稱m為a、b的“黃金大數”，n為a、b的“黃金小數”.當b-a=2時，a、b的黃金大數與黃金小數之差m-n=______.

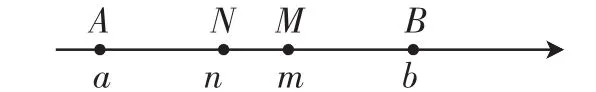
圖1

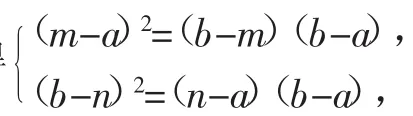
學生的困惑：此法先把各線段的長用代數式表示出來，再分別代入到已知條件中，列出方程組求解，這個答案顯然違背題意，這到底是什么原因呢？

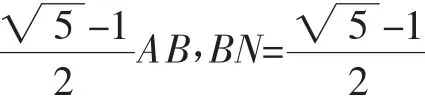
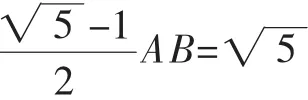
對于本題，還可以求出AB，然后列出關于AM、BN的方程，再求解.把已知AM2=BM·AB及BN2=AN·AB看作關于AM（或BM）或AN（或BN）的一元二次方程，即可求出線段AB上任意一條線段.

另解1：由AM2=BM·AB，BM=AB-AM，得AM2=（ABAM）·AB.又AB=b-a=2，則AM2=（2-AM）×2，解得AM=-1.根據對稱性，得BN=-1.則MN=AM+BNAB=2-4.

另解2：設MN=x，AN=y，則（x+y）2=2（2-x-y）.將“x+y”視為整體，整理得（x+y+1）2=5，解得x+y=-1（負值不合題意，舍去）.所以MB=2-（x+y）=3-.根據對稱性，得AN=3-.所以MN=AB-AN-MB=2-（3-）-（3-）=-4.

盡管得到的“答案”很明顯是錯誤的，但查找錯因并不那么容易.通過嚴謹的數學思考和基于對稱視角分析，不僅查明了真相，還收獲了借助對稱性來思考問題，及對稱觀念引領下的簡單解法，可謂一舉多得，下面再看一例.

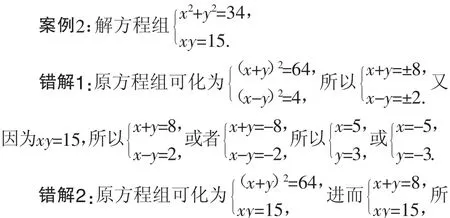
學生的困惑：錯解1、2的解是怎樣丟掉的？錯解3怎么多了四個解呢？

錯因分析：第一個學生“由xy=15，得到x、y同號，進而想當然推出x+y與x-y也同號，從而丟掉了兩個解”.事實上，x、y同為正數或x、y同為負數；當x、y同為正數時，可以得到x、y的和是正數，但x、y的差呢？并不一定是正數啊.同樣，當x、y同為負數時，x、y的和是負數，但x、y的差也不一定是負數.第二個學生忽視“正數有兩個平方根……”這一平方根的性質.第三個學生“解方程組的過程中，第2個方程兩邊平方了，因此求得方程組的解之后，必須代入原方程組進行檢驗，因此結合x、y必須取同號的值，必須舍掉異號的四個解”.在解題過程中，應隨時注意整體與局部的關系，不能以局部的性質代替整體，從而有效規避錯誤.

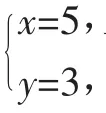
學生如有從對稱的角度分析問題的意識，則成功解題易如反掌，對稱在數學解題中的應用不勝枚舉.如2014年泰州卷第16題：

如圖2，正方形ABCD的邊長為3cm，E為CD邊上一點，∠DAE=30°，M為AE的中點，過點M作直線分別與AD、BC交于點P、Q.若PQ=AE，則AP等于______cm.

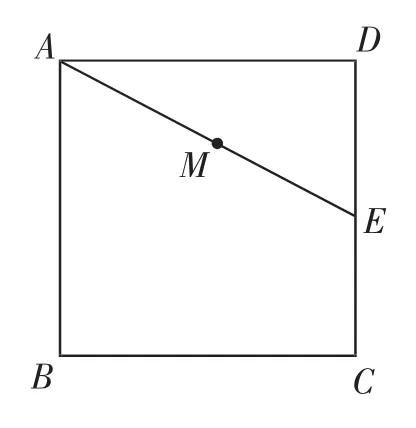
圖2

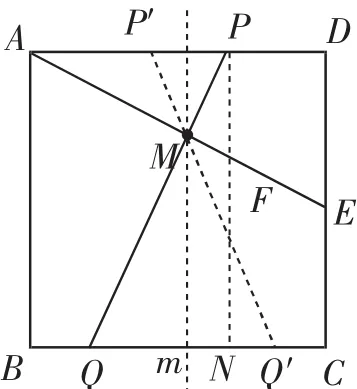
圖3

賞析：如果能從對稱的視角來理解則事半功倍（如圖3，兩次利用對稱，第一次是P′Q′與PQ關于直線m對稱，第二次是AP′與PD對稱），否則，要么容易忽視“確定性”或因思維定式導致丟解，要么事倍功半，即使做出來了，也耗時過多，造成“隱性丟分”，得不償失.關于本題的研究，錢德春老師在參考文獻［4］中已有詳細論述，這里不再贅述.

又如概率中用列表法和樹狀圖法求概率，列出的表格和樹狀圖從數學的角度來看是對稱的.

如圖4，一只螞蟻自由自在地在用七巧板拼成的正方形中爬來爬去（每一塊的表面完全相同）.

（1）分別計算它最終停留在1號板和2號板上的概率；

（2）它最終停留在3號板上的概率是多少？

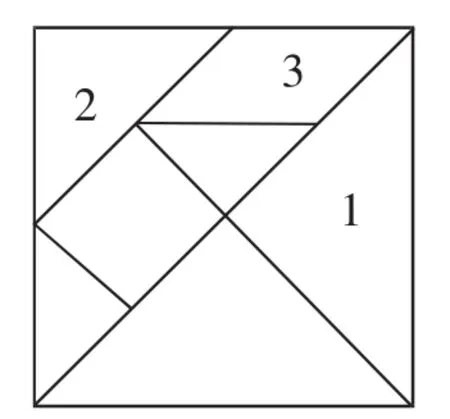
圖4

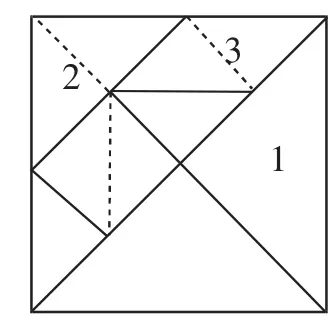
圖5

分析：如圖5，加上這三條輔助線后，借助對稱便直觀地看出停在2、3號板上的概率分別是多少了.

又如，求滿足（n+1）n2-2n-3=1的整數.

錯解：由x0=1，x≠0，得n2-2n-3=0，且n+1≠0，解得n=3.

分析：對于ab=1，上述解法只考慮了非零數的零次方等于1，而忽略了底數n+1等于1（指數為任意數）和-1（指數為偶數）的情況.如果想象有一條數軸，那么1、-1是關于原點對稱的.

總之，對稱，是觀念，也是方法，是一種或圖或式的靈活運用，在對稱視角下辨析錯因，澄清了錯誤，走出了困惑，同時開闊了視野，豐富了解題思路.

二、教學建議

1.解題教學要理解基礎知識，重視等價轉化，探索一題多解

通過對錯解引發的一題多解的分析，發現學生的學習問題，其根源是沒有重視等價轉化，思考不嚴密或基礎知識不扎實.轉化有等價轉化與非等價轉化兩種形式.等價轉化要求轉化過程中前因后果是充分必要的，才能保證轉化后的結果仍為原問題的結果.非等價轉化其過程是充分或必要的，要對結論進行必要的修正（如分式方程化為整式方程可能會出現增根，因此要驗根），它能給人帶來思維的閃光點，找到解決問題的突破口.但是一定要注意轉化的等價性與非等價性的不同要求，實施等價轉化時確保其等價性，保證邏輯上的正確（如案例1中的錯解，看似經得起推敲卻百密一疏，又如案例2及參考文獻［3］中對“解”的“純粹性”與“完備性”的分析）.等價轉化思想方法是高中數學解題的基本方法，在歷年高考中也常見，因此我們要不斷培養和訓練學生自覺的轉化意識，這有利于強化解決數學問題中的應變能力，提高思維能力和技能、技巧.

2.解題要讓學生學會自覺分析，揭示數學本質

學生解題水平取決于對知識本質的理解.案例1、案例2及參考文獻［3］中的錯解，這些錯誤產生的原因都是隱性的.羅增儒教授說過數學解題不僅要關注“答案”，更要對過程進行“自覺分析”.因此數學解題要讓學生養成自覺分析、反思質疑的良好習慣.從核心知識和概念入手，深挖教材，設計核心例題，充分揭示數學本質（如本文中的對稱思想、等價轉化思想等）.站在教育者的角度，數學本質應該包括數與形的客觀規律，知識所處的背景、地位、作用、聯系、區別及其蘊含的數學思想方法、思維過程.

3.解題教學要揭示數學思想方法與思維的形成

解題教學要推動學生經歷知識的形成過程，引導學生發現數學規律、知識的內在聯系和問題的解決途徑，促進數學思維的正遷移，滲透學習方法，轉換視角，借助數學思想化錯、融錯、究錯，使學生在科學精神、思維能力、情感態度與價值觀等方面得到進步；體會解決問題的過程，學會數學的表達和交流，積累經驗；在掌握“四基”的同時提高數學素養，實現更高層次的思維突破.

4.解題要注重生成，教學相長

數學問題都是運用所學過的知識加以解決的，知識轉化才是一切轉化思想與方法的本源.學生參與的解題活動不僅包括外顯的、可觀察的解題過程，也包括學生積極展示內隱的思維活動.作為一線教師，要想讓學生做到“吃一塹，長一智”，不僅要會講授，更要學會“傾聽”，要大膽放手，讓學生嘗試.布魯納說過：“學生的錯誤都是有價值的.”著名教育家卡爾·威特的教育秘訣之一，就是寬容地、理性地看待孩子的一切，包括錯誤.錯誤也從一定角度反映出學生對知識的掌握程度及暴露出來的教與學方面存在的問題.因此要善待學生的出錯，讓錯誤成為轉機，充分體現轉化思想，重視生成性資源的教學，采用逐步深入糾錯的方法，讓學生樂于糾錯，踏實糾錯.學生的主動好學定能讓數學課堂出彩.在教學中要教會學生進行錯解分析，挖掘錯誤的根源，從而鞏固和加深基礎知識，真正做到教學相長.總之，通過辨析錯解產生的原因，訓練學生思維的嚴謹性、深刻性、靈活性、批判性與獨創性，使學生的數學素養得到提升.以上論述還很粗淺，希望得到批評與指正.