關于與機械能守恒相關的一些問題的探討

趙 堅

(昆明市五華區基礎教育科學研究中心,云南 昆明 650031)

1 問題提出

涉及機械能守恒和機械能守恒定律的相關問題討論一直是大學普通物體教學中受到大家熱議的話題,[1～14]《大學物理》雜志曾經多次刊登文章進行討論,并先后4次以編輯部編者的話進行綜述說明．[15～18]近年來,此方面的問題又再次引發大家熱議,[19～25]特別值得重視的是,在中學物理教育界顯得尤為突出,較為混亂．歸納起來,大致有這樣幾方面的問題: (1) 機械能守恒或者機械能守恒定律是否滿足力學相對性原理; (2) 不同慣性系中機械能是否都滿足守恒; (3) 僅重力或彈簧彈力作用下的機械能守恒在各慣性系中是否都成立; (4) 機械能守恒定律滿足協變性嗎?等等．鑒于弄清楚這些問題對中學物理教師正確理解機械能守恒和機械能守恒定律以及開展好教學工作具有積極意義,故本文試圖就涉及機械能的一些相關問題在此作點探討．

2 問題探討

(1) 如何理解和看待機械能、機械能守恒和機械能守恒定律3個物理概念.

《中國大百科全書·物理學》中對此這樣表述:“機械能(mechanical energy)宏觀的動能與勢能之和”“機械能守恒(mechanical energy conservation of)質點或質點系在勢力場(保守力場)中運動時,其動能與勢能的總和恒為常量．動能與勢能的總和稱為機械能,故稱機械能守恒．在一個不受外界作用的封閉系統經歷任何變化過程中,系統的各種能量形式可以相互轉化,但所有能量的總和不變,這是普遍的能量守恒定律,機械能守恒只是它的一個特例”．可以看出,其一,機械能是一個力學范疇內的物理量,它由宏觀的動能與勢能構成;其二,所謂機械能守恒是指在滿足守恒的約束條件下,動能、勢能變化過程中,動能與勢能的總和恒為常量(保持不變);其三,機械能守恒只是能量守恒定律的一個特例,既然是特例就不具備作為普遍定律的一般性質,因此,在經典力學中雖然將機械能守恒定律作為一條定律來稱謂,但是它不同于能量守恒定律、動量守恒定律、質量守恒定律等作為自然界最普遍、最重要的基本定律所具有的普遍物理特性．因為,一個守恒定律常常是宇宙中某種對稱性的結果,守恒定律是表述運動方程的那些非常普遍的、重要的結果的一種方式,正如動量守恒定律可以理解為是伽利略不變性原理的一個直接結果．對能量守恒定律(energy conservation law)(熱力學第一定律)來說,它雖然指在一個封閉(孤立)系統的總能量保持不變．可是在理解上,其中總能量一般說來已不再只是動能與勢能之和,而是靜止能量(固有能量)、動能、勢能3者的總量．普遍意義下的能量守恒定律的表述是:一個系統的總能量的改變只能等于傳入或者傳出該系統的能量的多少．總能量為系統的機械能、內能及除內能以外的任何內能形式的總和．而對于一個特殊的、處于孤立環境下的系統,即不可能有能量或質量傳入或傳出系統．對于此情形,我們才將能量守恒定律表述為:“孤立系統的總能量保持不變．”所以,機械能守恒亦或機械能守恒定律要作為普遍意義下的物理定律,它必須有其普遍的物理特性才行．如果無視這些前提條件而去討論機械能守恒作為定律的諸多問題顯然都是無意義的．事實上,正是由于缺乏對相關問題的深入理解而在普通物理和基礎物理范疇將機械能守恒與機械能守恒定律混用,才是直接導致出現混亂的原因之所在．

(2) 不同慣性系中機械能都守恒嗎?機械能守恒具有相對性嗎?機械能守恒定律滿足力學相對性原理嗎?

引發這一系列問題的焦點主要是針對下述幾個習題中出現的問題．

例1.如圖1所示,固定在車廂內的光滑斜面,傾角為θ,車廂以速度v0勻速前進,斜面上質量為m的滑塊從斜面頂端自由滑下,試分析:以地面為參考系,滑塊在下滑過程中機械能是否守恒?

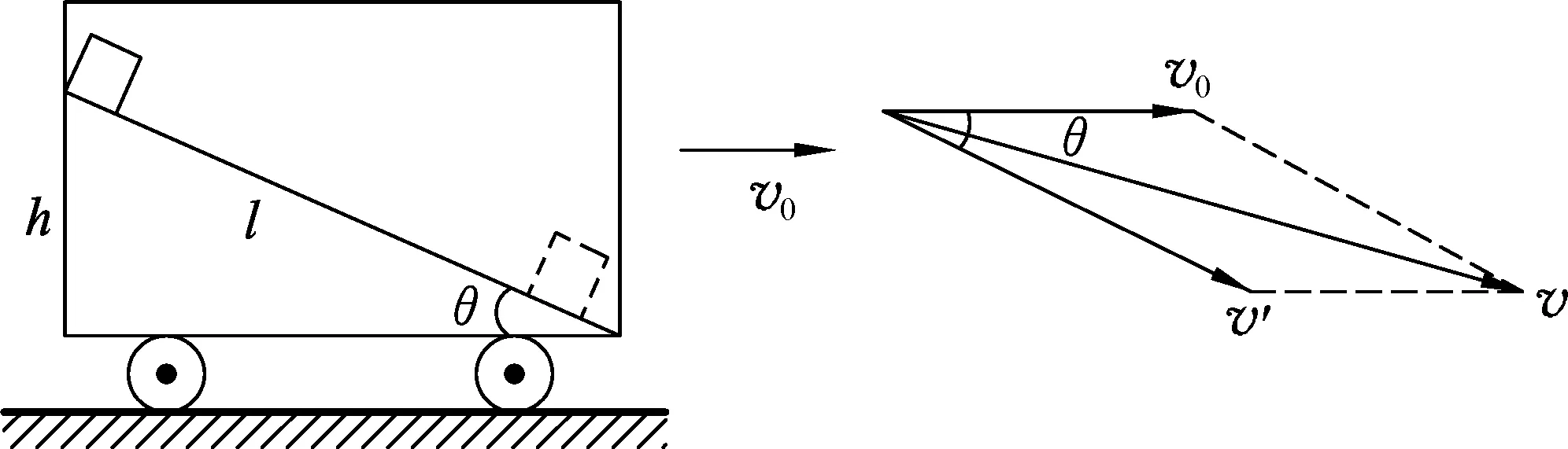
圖1 圖2

以地面為參考系,滑塊在斜面頂端時機械能為

滑塊在斜面底端時的機械能為

式中v為滑塊滑到斜面底端時對地的速度．根據運動合成,其大小為滑塊在斜面底端時對車廂的速度v′和車廂速度v0的矢量和,如圖2所示．

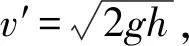
可見,E2>E1,以地面為參考系,滑塊的機械能不守恒．

為此產生困惑,因為“根據力學相對性原理,任何力學規律在任一慣性系內具有相同的形式．機械能守恒定律作為重要的力學規律,理應滿足力學相對性原理．既然車廂和地面都是慣性系,為什么機械能守恒定律在車廂參考系內成立,而在地面參考系中不成立呢?”

圖3

例2.如圖3所示,在車廂里光滑桌面上彈簧拉著一個物體m作簡諧運動,車廂以勻速v前進．

例3.如圖4所示,以速度v0勻速下降的升降機天花板上懸掛著一個質量為m的小球,某時刻小球突然下落,在小球下落過程中(未碰升降機地板前):

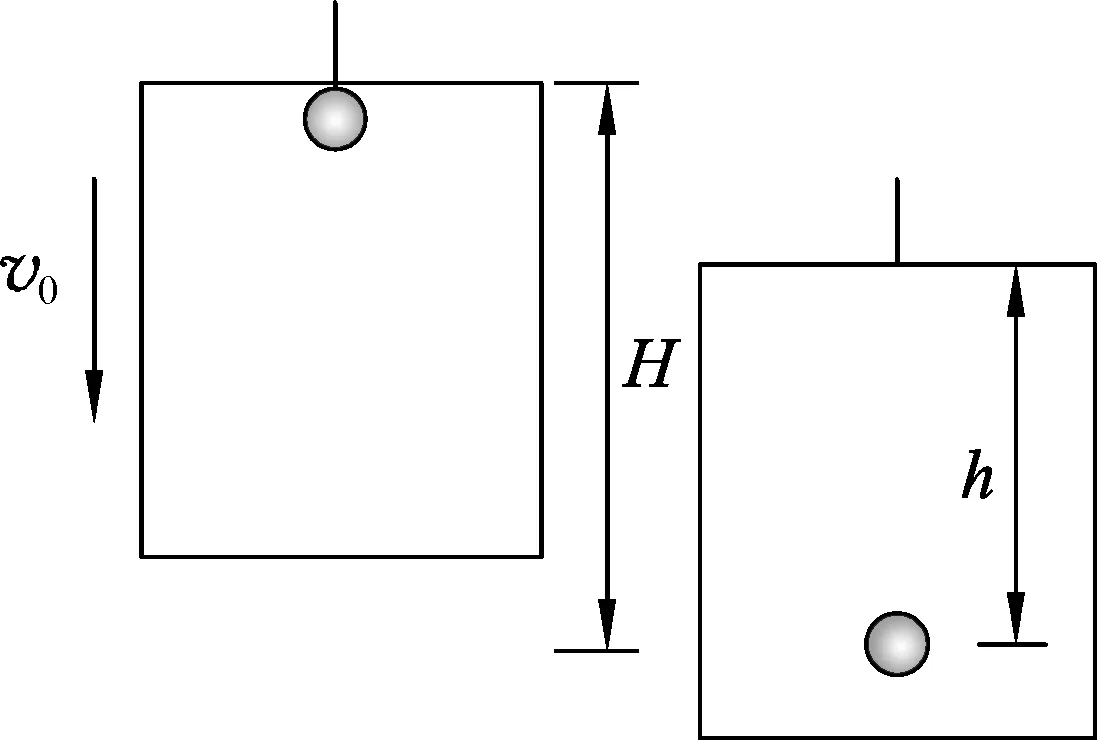
圖4

以升降機為參考系,只有重力做功,小球機械能守恒,有

式中h為小球相對升降機下落的高度,v為小球相對升降機的速度．

以地面為參考系,設小球在下落瞬間的機械能為E1,則

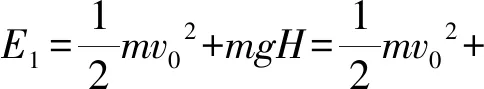
可見,E2=E1,即以地面為參考系,小球的機械能仍是不變的,為什么會是這樣?

以上幾個例子,集中反映出這樣幾個問題．其一,例1、例2中當參考系發生變化后,研究對象的機械能不再相等,是否機械能守恒具有相對性?不滿足力學相對性原理?其二,例3中雖然研究對象參考系發生變化,但其機械能仍然滿足相等,是否力學相對性原理僅僅是針對研究對象只受到重力作用的這類特殊情形才是成立的?其三,機械能守恒定律滿足力學相對性原理嗎?

認真分析上述3個例子,我們會發現,在例1中如果以地面作為參考系,則斜面對滑塊的支持力已經對滑塊做了功,不再滿足質點或質點系在勢力場(保守力場)中運動時,其動能與勢能的總和恒為常量的機械能守恒條件,導致滑塊的機械能發生變化;假如斜面對滑塊的支持力對滑塊不做功,滑塊的機械能必定是保持不變的．例2中小球與彈簧系統之所以在不同參考系中機械能不同,原因在于在地面系中觀測,彈性勢能不僅與小球的空間坐標用有關,還與小車運動有關,即彈性勢能顯含時間t,且產生彈力的胡克力場場源(車廂壁)具有速度v,除非小車不動v=0,這樣,在兩個參考系觀測結果一定是相同的．可是,問題又來了,例3中重力勢能也是一個顯含時間t的量,為什么以地面為參考系時小球機械能仍保持不變?這也是容易讓大家感到比較糾結的問題．對此,朱如曾先生提出:[21]“在外力場概念下質點的重力勢能就是內力場概念下質點與地球之間的相互作用勢能．內力勢能由系統中各對質點之間的距離決定,而與系統中各質點的速度無關．由于參考系(慣性系和非慣性系)的變換完全不改變系統中各對質點之間的距離以及相互作用力,所以內力勢能具有參考系變換下的不變性(即在不同參考系同時觀察同一系統的內力勢能是相等的),亦即對同一系統,不同參考系中的勢能(內力勢能及根源于內力場的外力勢能)具有參考系變換下的不變性．”

另外,一切普遍規律(微分方程)都是協變的,此點無容置疑,如能量守恒定律(普遍表述是“一個系統能量的變化等于非保守外力作功”,不能理解為“能量不變(守恒)”)．但是加上一些不協變的條件(初始條件、邊界條件、規范條件等),就不協變了．因為,能量不變(守恒)涉及3個問題:(a) 系統的選擇,(b) 什么是保守力?(c) 做功的條件,而我們只有對選定的系統才能區分內力和外力．我們通常說保守力作功與路徑無關,是指沿路徑的積分是“等時”的,也就是在某一個時刻,沒有考慮時間的變化．如例3中,在電梯內自由落體問題里,若忽略重力與高度有關,無論在電梯參考系還是地面參考系里,重力場都是非時變的,因此能量都守恒．同時,保守力一定是個有勢力場,而只有不含時間的力場才能保證能量不變,否則能量必然變化．如例2中,在車內彈簧振子問題里,選彈簧和振子為系統, 在地面的參考系里看外力著力點在動; 只選振子為系統, 在地面的參考系里看彈性力勢場是時變的,因此能量不守恒．再有,不作功的條件是受力作用點不動,或力垂直于位移．在例1中,車內光滑斜面下滑物體問題里,從車的參考系里看斜面的支撐力垂直于斜面,在地面的參考系里看斜面的支撐力并不垂直于斜面．

綜上所述,筆者贊同這樣一個觀點[18]:“所以規律都服從相對性原理”,然而只有“普遍定律滿足協變性”“非普遍定律不滿足協變性,但可以導出”．

致謝:本文初稿得到北京大學趙凱華先生認可,同時就一些細節與趙先生進行多次有益探討,并得到趙先生的悉心指導,借此深表感謝!