用微元數值計算法研究行星橢圓軌道運動
朱佳平 林輝慶
(杭州市余杭高級中學,浙江 杭州 311100)
1 高中物理非線性問題
由于數學知識的限制,高中物理定量研究的問題,一般是物理量不隨時間變化或隨時間均勻變化的情況.高中物理還涉及很多的非均勻問題,在這些問題中,物理量隨時間的變化不均勻,或者說,物理量的變化率不是常數.
對于非均勻問題,教科書一般只作定性介紹或直接給出結論.高中學生具有強烈的求知欲望,對于這些教科書中只作簡略介紹的內容,他們迫切希望進一步了解其中的奧妙.例如,對于萬有引力定律.
如何用高中學生能接受的方式研究非均勻問題,以滿足學生的求知欲,是高中教學需要探討的問題.
2 行星運動軌跡計算
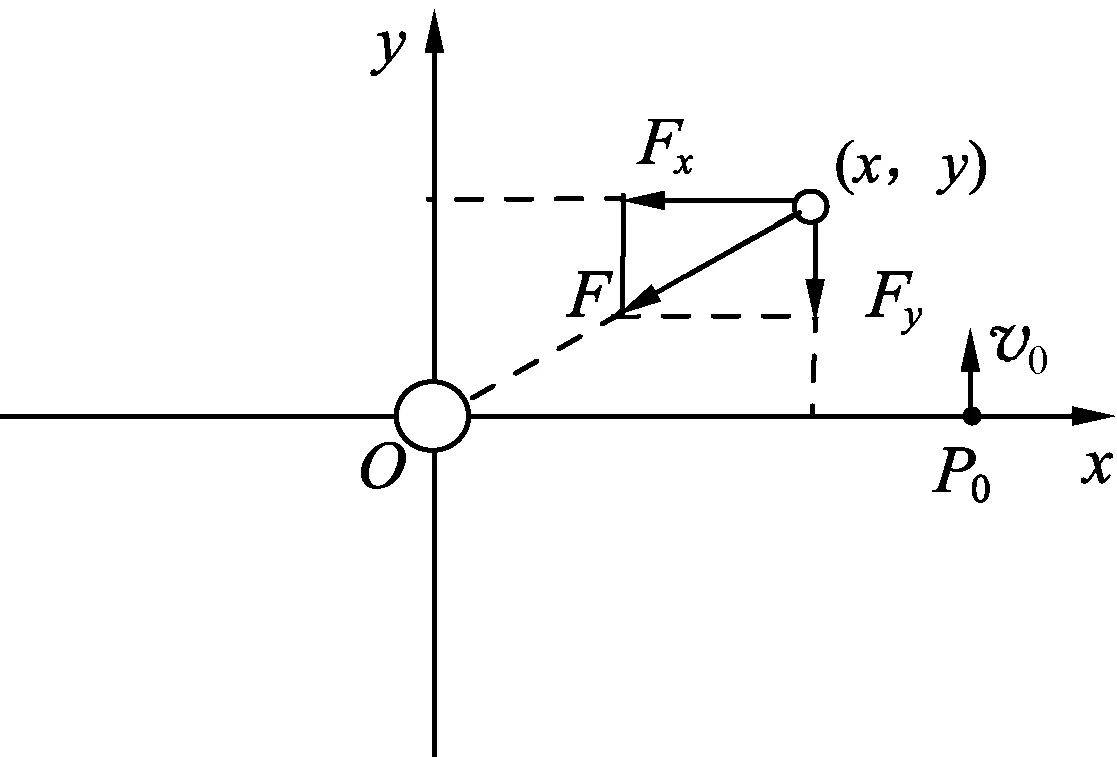
圖1 行星收到太陽的引力

設行星在t=0時刻的位置為P0(x0,y0),速度為v0(vx0,vy0).在隨后的一段很短時間Δt內,行星的加速度可以看作不變,它在x軸和y軸的分量分別為
(1)
在Δt時間內,行星在x軸和y軸的平均速度分別為
(2)
在t1=Δt時,行星運動到P1點,坐標為
(3)
在第2個Δt時間內,行星的加速度仍然看作不變,它在x軸和y軸的分量分別為
(4)
行星在x軸和y軸的平均速度分別為
(5)
在t2=2Δt時,行星運動到P2點,坐標為
(6)
同理可以求出t3=3Δt、t4=4Δt……行星的位置坐標.用這些數據就能在坐標平面上作出行星的運動軌跡.[1]

利用Excel的“插入散點圖”即可畫出行星運動軌跡如圖2.可以看出此時行星的運動軌跡為橢圓,初始位置為近日點.
保持x0=0.500,y0=0,vx0=0和Δt=0.1不變,只要改變初速度vy0的數值,就可得到行星的初速度小于和等于“第一宇宙速度”v1、等于和大于 “第二宇宙速度”v2時的運動軌跡,它們分別是以初始位置為遠日點的橢圓、圓、拋物線和雙曲線.
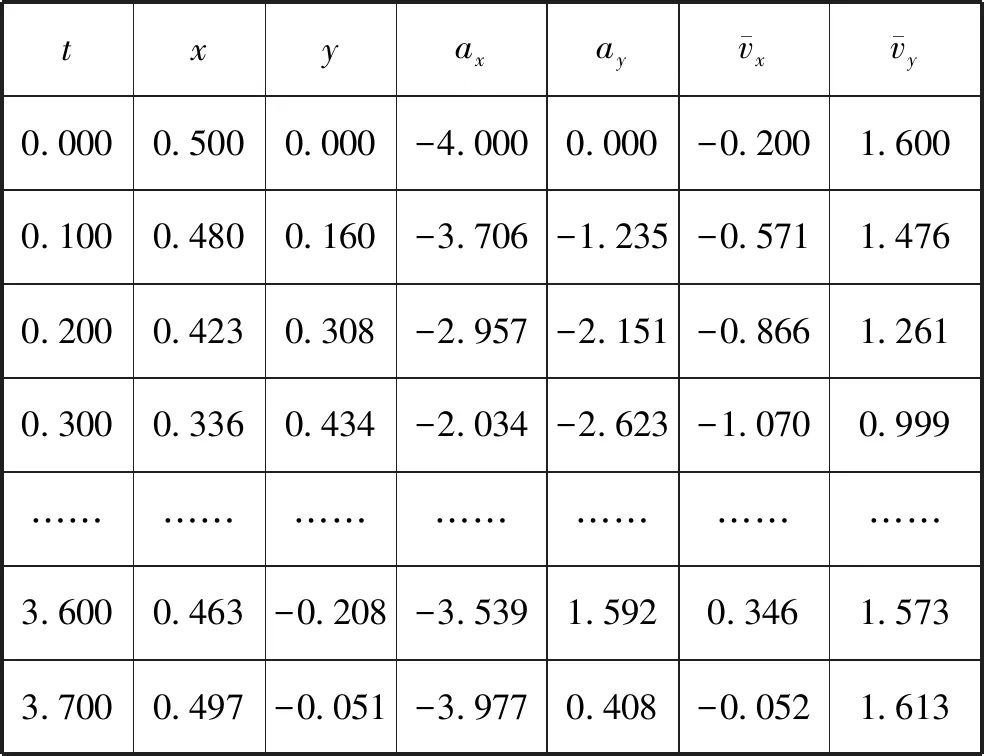
表1 行星不同時刻的位置坐標

圖2 行星的橢圓軌道
3 微元數值計算法
上述計算行星運動軌跡的方法叫作微元數值計算法.
微元數值計算法的要點有兩個:一是通過取微元“化變為恒”.將一個隨時間t作非線性變化的過程分割為很多個微小的過程,這樣的微小過程叫作微元,微元的時間用Δt表示.在各個微元中,物理量可以看作均勻變化,即變化率可以看作恒定不變.二是數值計算.當已知了過程在t0=0時各個物理量的數值,由物理規律算出這些物理量在t0=0時的變化率.然后選取一個恰當的微元Δt的數值,由各物理量在t0=0時的變化率計算出它們在t1=Δt時的數值.由此又可以計算出它們在t1=Δt時的變化率和t2=2Δt時的數值……用這些數值就可以畫出各物理量隨時間的變化圖線或任兩個物理量之間的變化圖線.[2]
可以看出,微元數值計算法的本質就是求積分,只是后者是Δt→0時的極限值,前者是近似值.由于我們在學校學習中所接觸的物理問題大多是能用解析式“精確”描述的,解析式對物理過程的描述是理想化的,是真實過程的近似.在微元數值計算法中,可以靠減小微元的數值或取平均值的方法來減小誤差,使結果的準確度達到我們的要求.
4 可行性、必要性與教學效果
4.1 可行性
通過高一物理第1章中瞬時速度概念和第2章中勻變速直線運動位移的學習,學生初步掌握了微元方法和極限概念,這為學習微元數值計算法打好了基礎.
在技術上,學生在初中就已經掌握了Excel工作表的功能和用法,能用它處理數據和作圖,這是用微元數值計算法研究問題的技術條件.
這樣,只要知道一個非均勻物理過程的變化規律,就能借助于Excel工作表或信息技術中其他數據處理工具,用微元數值計算法求出這個過程各個物理量的具體變化情況.
4.2 必要性
真實的過程總是復雜的,絕大多數不能用函數的解析式描述.對這些問題的定量研究,都需要用微元數值計算法求得各個量在不同時刻的數值,描繪出它們隨時間變化的圖像.隨著計算機運算能力的提升,用微元數值計算法解決實際問題的范圍隨之不斷擴大,準確度不斷提高.因此,微元數值計算法是實際生產和研究中常用的方法,高中學生有必要了解這種科學方法.
4.3 教學效果

用微元數值計算法求解復雜的非均勻問題,能極大地滿足學生的求知欲,使他們深切地體驗自然的奧秘和人類智力的偉大,從而增強探索自然奧秘的動力.
信息化是當今社會的主要特征之一.運用信息技術解決復雜物理問題的實踐,能有效培養學生在生活、生產和研究中主動運用信息技術工具的意識和能力.

