對一道高考題的多解探究

☉浙江省玉環市玉城中學 張夏飛

我國南宋時期杰出的數學家楊輝曾說：“夫學算者，題從法取，法將題驗，凡欲明一法，必設一題.”其實，在教材中所選用的例題、練習題都是經過專家們再三選取、提煉而來的，能幫助我們有效地明晰概念、掌握方法.充分感受教材中所選用的例題、練習題中豐富的內涵，從而達到舉一反三的目的，并提高分析問題和解決問題的能力.

一、高考真題

（2018·全國Ⅲ卷文、理·22）在平面直角坐標系xOy中，⊙O的參數方程為θ為參數），過點（0，且傾斜角為α的直線l與⊙O交于A，B兩點.

（1）求α的取值范圍；

（2）求AB中點P的軌跡的參數方程.

本題以參數方程與普通方程的互化為問題背景，通過直線與圓的位置關系、中點弦問題來考查化歸與轉化思想、運算求解能力以及數學運算與直觀想象等數學核心素養.

二、官方標答

解：（1）⊙O的直角坐標方程為x2+y2=1.

（2）方法1：l的參數方程為（t為參數

設A，B，P對應的參數分別為則，且滿足

又點P的坐標（x，y）滿足

所以點P的軌跡的參數方程是（α為參數

點評：第（2）小題求解AB中點P的軌跡的參數方程，借助直線l的參數方程與普通方程的轉化，采用韋達定理，并結合中點坐標公式，通過三角恒等變換的轉化來確定點P的軌跡的參數方程.其實，解決第（2）小題中AB中點P的軌跡的參數方程問題，切入點各異，方法眾多.

三、巧思妙想

1.解幾思維

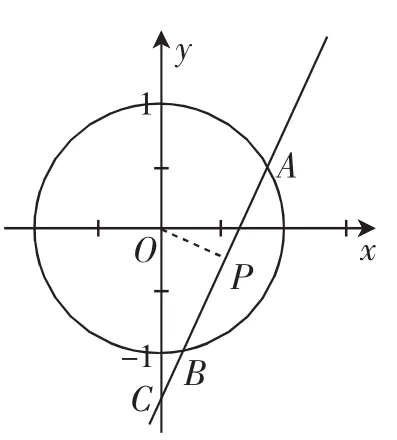
圖1

（2）方法2：由題知⊙O的直角坐標方程為x2+y2=1，設點C的坐標為連接OP，由于P是AB的中點，則有OP⊥AB.

設P（x，y），當P不為O點時，設OP的直線方程為y=kx，則CP的直線方程為

而點P在⊙O內，所以AB中點P的軌跡方程是x2+y2+其對應的參數方程為β為參數，0＜β＜π）.

點評：通過平面幾何中的垂徑定理，利用解幾法中的交軌法，結合相應的直線方程來確定對應的P（x，y）的軌跡方程，并結合兩圓相交弦所在的直線方程以及圖形直觀來確定參數y的取值范圍，進而把普通方程轉化為對應的參數方程即可得以解決.

2.設而不求思維

（2）方法3：由題知⊙O的直角坐標方程為x2+y2=1.

設P（x，y），A（x1，y1），B（x2，y2），則x12+y12=1，x22+y22=1.

兩式相減可得x12-x22+y12-y22=0，即（x1+x2）（x1-x2）+（y1+y2）（y1-y2）=0.又

而點P在⊙O內，所以AB中點P的軌跡方程是x2+y2+其對應的參數方程為β為參數，0＜β＜π）.

點評：通過設出相應點的坐標，利用設而不求的思維，通過中點弦中的點差法建立關系式，并結合中點坐標公式與直線的斜率公式加以轉化來確定對應的點P（x，y）的軌跡方程，結合兩圓相交弦所在的直線方程以及圖形直觀來確定參數y的取值范圍，進而把普通方程轉化為對應的參數方程即可得以解決.

3.函數方程思維

4（1+k2）＞0，即k2＞1，從而即，代入，可得

所以將其代入，整理可得x2+y2+

又因為k2＞1，所以＜0，即所以AB中點P的軌跡方程是

所以AB中點P的軌跡方程是其對應的參數方程為β為參數，0＜β＜π）.

其實，在日常解題過程中，應不滿足于一種解法，多思則多解，這樣在遇到具體問題時才能真正做到隨機應變，從而達到快速求解的目的.充分運用一題多解，可以從多角度、多途徑尋求解決問題的不同方法.同時，從多種解法的對比中選取最佳解法、通性通法、特殊解法等，總結解題規律，提高分析問題、解決問題的能力，真正達到思維的發散性和創新性，培養數學核心素養.F