截面法在求解空間幾何體外接球問題中的應用

☉湖北大學附屬中學 楊彩云

縱觀近幾年的高考題和各地的調考題，發現空間幾何體的外接球問題一直是命題的熱點之一.命題的綜合化趨勢也越來越明顯，要求學生同時具備較強的閱讀理解能力和空間想象能力、精準的作圖能力、準確的計算能力，才能順利地完成解答.

以下以高考題和調考題中精選的熱點考題為載體，通過截面法找球心，來對常見的三類空間幾何體的外接球問題進行探究，歸納出運用截面法找球心、求解幾何體的外接球半徑R的常見的三種類型及相應的解題策略.

首先給出需要用到的相關的重要性質：

性質1：過小圓圓心且垂直于小圓平面的直線過球心（類比：圓的垂徑定理）.

性質2：球心在以截面圓圓心為垂足的截面圓的垂線上，且球的半徑R、截面圓的半徑r及球心到截面圓的距離d滿足：R2=r2+d2.

性質3：在同一個球中，過兩截面圓的圓心垂直于相應的圓面的直線若相交，則交點是球心（類比：在同圓中，兩相交弦的中垂線的交點是圓心）.

類型一：已知三棱錐中一條側棱垂直于底面

例1已知三棱錐S-ABC的所有頂點都在球O的球面上，且SC⊥平面ABC，若SC=AB=AC=1，∠BAC=120°，則球O的表面積為______.

解析：如圖1所示，設△ABC的外接圓的圓心為O1.

因為AB=AC=1，∠BAC=120°，

所以O1B=1.

因為SC⊥平面ABC，OO1⊥平面ABC，SC=1，

所以∠ABC=30°.

所以△ABC的外接圓的直徑

所以r=1.

因為△OSC為等腰三角形，

所以球O的表面積S=4πR2=5π.

由上述例題可知，對于第一種類型：已知三棱錐中一條側棱垂直于底面的模型，解題策略如下：

1.過底面外心作底面的垂線；

2.利用正弦定理求出底面外接圓的半徑r；

3.求出球心到底面的距離d（d為側棱長的一半）；

4.運用R2=r2+d2求出球的半徑.

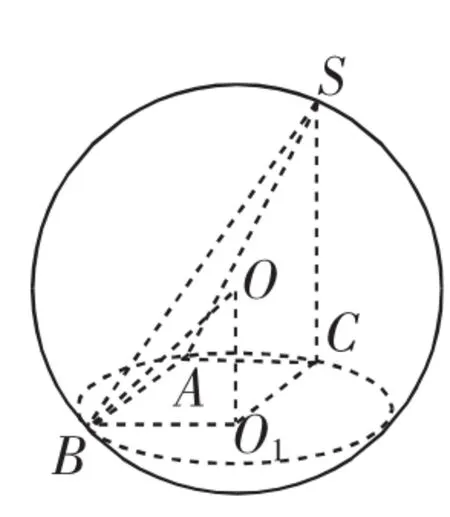
圖1

圖2

類型二：已知三棱錐中兩個平面所成二面角的大小為90°，即這兩個平面互相垂直

例2在四面體ABCD中，AD=DB=AC=CB=1，則當四面體ABCD的體積最大時，它的外接球半徑R=______.

解析：如圖2所示，取AB的中點E，連接CE，DE.

設AB=2x（0＜x＜1），則

因為當平面ABC⊥平面ABD時，四面體的體積最大，所以

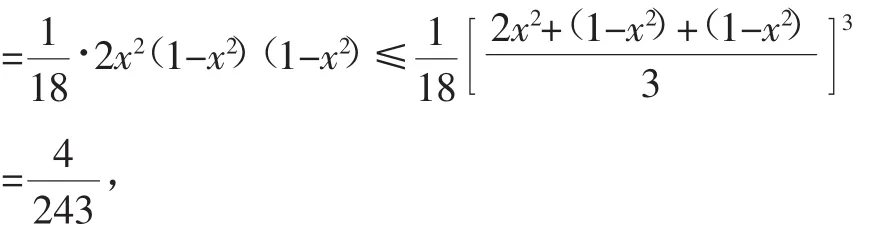
當且僅當2x2=1-x2時，取等號，

設△ABD的外心為G，△ABC的外心為H，分別過G，H作平面ABD、平面ABC的垂線，交于O點，則O為四面體ABCD的外接球的球心.

在△ABD中，有

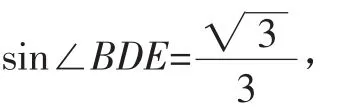
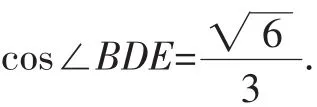
所以

所以

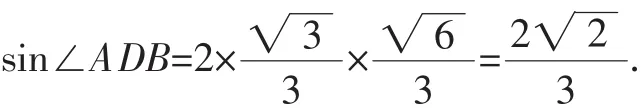
設△ABD的外接圓的半徑為r，

則，即

又

所以

所以四面體外接球半徑

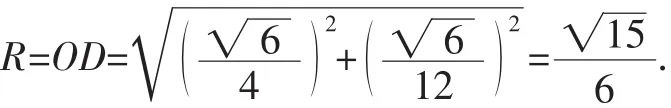
因此，對于已知三棱錐中的兩個平面所成二面角為90°，即這兩個平面互相垂直的模型，解題策略是：

1.過這兩個面的外心分別作這兩個面的垂線，交點就是外接球的球心；

2.求出這兩個面的外接圓圓O1、圓O2的半徑r1、r2；

3.構造矩形利用幾何關系求出d（d為O2到兩個互相垂直的平面交線的距離）；

4.運用R2=r12+d2求出球的半徑.

類型三：已知三棱錐中兩個平面所成二面角的大小（不為90°）

例3已知邊長為的菱形ABCD中，∠A=60°，現沿對角線BD折起，使得，此時點A，B，C，D在同一個球面上，則該球的表面積為（ ）.

解法一：如圖3所示，取BD的中點F，連接AF、CF，則AF⊥BD且CF⊥BD，AF=CF=3.

所以∠AFC=120°.

分別在CF、AF上取三等分點，使得

所以O1、O2分別為△BCD、△ABD的外心，且O1C=2，O1F=O2F=1.

分別過O1、O2作平面BCD、平面ABD的垂線，且兩條垂線交于點O，則點O為四面體ABCD的外接球球心，連接

所 以 在 Rt△OO1C中

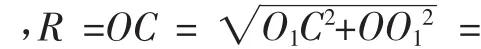
所以四面體的外接球的表面積為4πR2=28π.故選C.

圖3

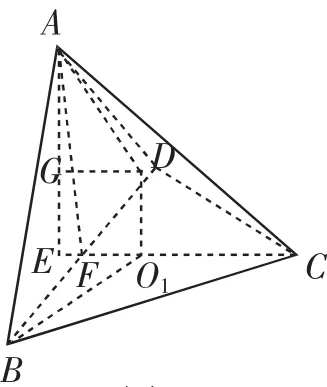
圖4

解法二：如圖4所示，取BD的中點F，連接AF，CF，則AF=CF=3.

因為，所以

過點A作AE垂直于CF的延長線于點E，則∠AFE=60°.所以

設等邊△BCD的外心為則

設三棱錐A-BCD的外接球球心為O，半徑為R，OO1=x，則OO1⊥平面BCD，過O作OG⊥AE于點G.則在Rt△OO1B中，有R2=x2+4，

在Rt△AOG中則有

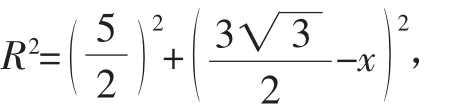
所以R2=7.

所以四面體的外接球的表面積為4πR2=28π.故選C.因此，對于已知三棱錐中兩個平面所成二面角的大小且不為90°，即這兩個平面互相不垂直的模型，解題策略有兩種：

策略一：找出這兩個面的外心，并過外心分別作這兩個面的垂線，交點就是外接球的球心，再通過幾何關系計算球的半徑.

策略二：找出其中一個面的外心，過外心作該面的垂線，構造出兩個直角三角形，并兩次利用勾股定理，聯立方程組求解球的半徑.

結合以上例題，可將截面法找球心的模型歸納為以下三種類型：

1.已知三棱錐中一條側棱垂直于底面；

2.已知三棱錐中兩個平面所成二面角的大小為90°；

3.已知三棱錐中兩個平面所成二面角的大小且不為90°.

總之，通過截面法找球心來求解幾何體外接球的半徑，應先畫出圖形，找出幾何體中的特殊元素，如直角三角形、等腰三角形，或者兩平面所成的二面角是特殊角等，再根據球的截面的性質，把立體幾何問題轉化為平面幾何問題，利用球的半徑R、截面圓的半徑r及球心到截面圓的距離d三者之間的關系R2=r2+d2，從而求得外接球的半徑.

空間幾何體的外接球問題在高考中常以多種方式出現.同一個問題，或許有多種解題思路，如果部分題目的難度再增加，可能還需尋求新的方法解決問題.高考復習中切忌好高騖遠，應當重視各種題型的備考演練，重視高考信息的搜集，不斷充實題目的類型，升華解題的境界.F