圓錐曲線中一類定點問題的探究
☉浙江省臨海市大田中學 葉偉飛
以圓錐曲線為背景的定點問題在近幾年的高考命題中經常出現,此類問題對考生分析問題和計算處理問題的能力要求較高.本文以橢圓背景下的一道定點問題為引例,從問題的多種解法、多種變式及結論等幾個視角進行探究.
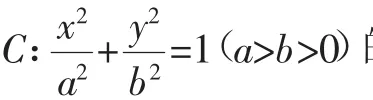
引例已知橢圓的離心率等于,經過其左焦點F(-1,0)且與x軸不重合的直線l與橢圓C交于M,N兩點.
(1)求橢圓C的方程;
(2)O為坐標原點,在x軸上是否存在定點Q,使得點F到直線QM,QN的距離總相等?若存在,求出點Q的坐標;若不存在,說明理由.
第(1)問橢圓C的方程為過程略),下面對第(2)問進行探究.
一、問題分析
思路1:若存在點Q,使得點F到直線QM,QN的距離相等,即點F到∠MQN的兩邊的距離相等,則QF為∠MQN的角平分線,∠MQF=∠NQF,即直線QM與QN的斜率互為相反數,進而找到解題的切入點.
思路2:如圖1所示,結合橢圓的對稱性,若滿足條件的點Q存在,則點N關于x軸的對稱點N′即為直線QM與橢圓的另一個交點P,即Q,P,M三點共線.
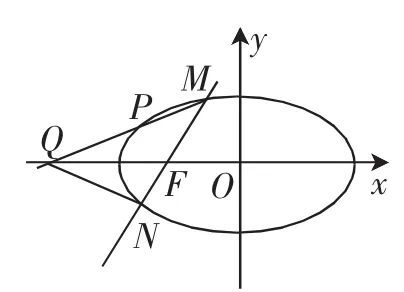
圖1
二、問題解答
針對上面兩種思路,得到如下兩種解法.
解法1:當直線MN斜率存在時,設直線MN的方程為
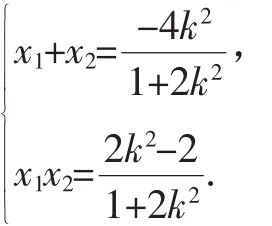
設Q(t,0).由點M,N在x軸異側,則問題等價于“QF平分∠MQN”,且x1≠t,x2≠t,又等價于
將y1=k(x1+1),y2=k(x2+1)代入上式,整理得2x1x2+
將根與系數的關系代入上式,整理得t+2=0,即t=-2,所以Q(-2,0).
當直線MN的斜率不存在時,存在Q(-2,0)也使得點F到直線QM,QN的距離相等.
故在x軸上存在定點Q(-2,0),使得點F到直線QM,QN的距離總相等.
解法2:設滿足條件的點Q存在,設Q(t,0),M(x1,y1),N(x2,y2),點N關于x軸的對稱點N′(x2,-y2),則共線.
設直線MN:x=my-1(m≠0),
則x1=my1-1,x2=my2-1,代入上式得
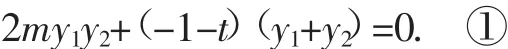
將直線MN與橢圓方程聯立得:消元得(m2+2)y2-2my-1=0.
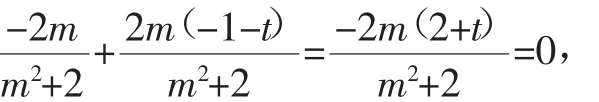
所以t=-2,Q(-2,0).
當m=0時,存在Q(-2,0)也使得點F到直線QM,QN的距離相等.
故在x軸上存在定點Q(-2,0)滿足題意.
三、結論探究
由第(2)問的結論發現無論直線l怎么旋轉,交點M,N與定點Q始終滿足題意,那么點Q與橢圓有何關聯?細心的讀者可能發現點Q為橢圓的準線與x軸的交點.基于此視角,下面對問題的一般結論進行探究.
結論1:F為橢圓的右焦點,過F的直線與橢圓C交于A、B兩點,點為坐標原點,則點F到MA,MB的距離相等.
本結論的證明,除了利用引例所述的兩種方法外,還可以利用橢圓的第二定義.
證明:如圖2所示,由橢圓的第二定義知
由
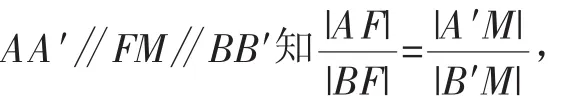
則∠AMA′=∠BMB′.
所以∠OMA=∠OMB.
所以點F到MA,MB的距離相等.
類似地,我們還可以將該結論拓展到雙曲線和拋物線中.
結論2:F為拋物線C:y2=2px(p>0)的焦點,過點F的直線與C交于A、B兩點,點為坐標原點,則點F到MA,MB的距離相等.證明略.
結論3:F為雙曲線的右焦點,過F的直線與C右支交于A、B兩點,點為坐標原點,則點F到MA,MB的距離相等.證明略.
四、變式探究
變式:已知橢圓的離心率等于,經過其左焦點F(-1,0)且與x軸不重合的直線l與橢圓C交于M,N兩點.
(1)求橢圓C的方程;
(2)O為原點,點Q(-2,0),M,N是橢圓上兩個動點,若直線QM與QN的斜率互為相反數,判斷直線MN是否過x軸上某定點.
解析:可設直線MN:y=kx+m與橢圓方程聯立得消元得
將y1=kx1+m,y2=kx2+m,代入上式得

所以m-k=0,即m=k.
所以直線MN過定點(-1,0).
綜上所述,通過對一道題目的多種探究,讓我們不僅明白了問題的多種求解思路,而且清楚了命題的根源,拓寬了解題的思路,落實了解題能力的提升.W

