如何從“冷飯”到“營養餐”
陳小燕
【摘 要】新課標從實驗稿到2011版,在“統計與概率”部分的調整包括容量減少和難度降低,與拉長和增加統計的學習,可能性即概率知識的學習,僅僅安排了一次學習。這部分內容該如何復習?豐富素材網羅多種概率模型,積累活動經驗,加強數據分析方法的指導,只有指向學科素養的教學才具有生命力。
【關鍵詞】實驗;體驗;數據分析
雖然幾年沒教六年級了,這學期卻有幸思考了六年級的一節“可能性”的復習課。備課時所見的僅僅是蘇教版六年級教材中的一頁復習內容,追溯蘇教版的教學內容,僅僅在四年級上冊進行過一次小單元的教學。不禁思考,僅教過一次,復習是否是將那盤新授的“冷飯”炒炒就好?答案顯然是否定的,從四年級到六年級,學生已經逐步形成了抽象思維,思維水平不同,對知識應當有更深刻的認識和理解。同時,六年級的復習是對整個小學階段數學學習的一個總結,同時也即將開啟第三學段數學的學習,具有承前啟后的作用。所以,我們需要站在更高的角度進行思考。仔細閱讀那一頁的復習內容:前兩題是基礎練習,復習簡單隨機事件的特點,通過列舉判斷簡單隨機事件發生的可能性的大小;第三題則是綜合運用可能性的知識解決實際問題;第四題則一反常序由摸球結果倒推球的組成,意在感受簡單隨機事件發生的可能性與事件發生頻率之間的聯系。不難窺見復習思路:基礎—應用—深化,正如教材只是一個例子,不同的人有不同的理解,教無定法,針對同樣的教學內容,我們需要充分發揮復習效用,將一盤冷飯變成營養餐呢?筆者有了如下的思考。
一、豐富素材——將“冷飯”炒熱
小學階段的數學教學,要通過重復試驗讓學生估計隨機事件發生的可能性大小。教材中,無論是蘇教版、浙教版還是北師大版,盡管編排不同,但都涉及了拋硬幣、擲骰子、摸球、玩轉盤等多種實驗素材。這些不同的實驗素材,其實屬于不同的概率模型,其中轉盤屬于幾何概型,其余屬于古典概型。幾何概型是連續的,可以分為無限等份,能形象直觀地幫助學生理解可能性的大小;古典概型則可能結果有限,是較為具體的模型。但這兩種模型都屬于理論概率模型,它們出現的可能性相等。其中,拋硬幣是結果最為簡單的等可能性模型,所以,比賽選場地常用這類簡單方便的方法。
但是,僅僅這樣的概率模型并不夠,生活中仍存在很多非等可能性的隨機事件,而這樣事件可能性的大小更依賴與對實驗數據的統計。對比蘇教版、浙教版、北師大三個版本,北師大版中有所體現,具體的有拋啤酒瓶蓋、天氣情況預測等。由于等可能性事件的結論較為明顯,經常讓學生失去實驗興趣;非等可能性事件對實驗的依賴,能幫助學生更好地理解隨機性。同時,對于可能性的判斷原自統計數據的分析,更能體現統計與概率二者之間的緊密關系。
不同的概率模型對學生理解可能性具有不同的幫助,豐富的素材網羅了多種概率模型,能幫助學生夯實基礎。
二、讓定性飛一會兒——將“冷飯”炒熟
新課標從實驗稿到2011版,在“統計與概率”部分的調整包括容量減少和難度降低,與拉長和增加統計的學習,如扇形統計圖的學習更為具體,卻減少了可能性即概率知識的學習,僅安排了一次學習。隨機思想是概率教學的核心,正所謂離開了隨機,就談不上概率。中科院院士陳希孺先生認為:統計學是有關收集和分析帶隨機性誤差的數據的科學和藝術。統計并非一成不變,應滲透隨機性,感受不確定事物遠遠多于確定事物,接納不確定性的存在。隨機思想的滲透應當貫穿于整個“統計與概率”部分,不僅在可能性的那一次學習時,同樣,隨機思想也是溝通統計和概率的橋梁。
六年級學生在學習了分數百分數后,對可能性大小的表示能述諸于數,能簡單地用0、100%表示極端可能情況,理解可能性大小處于極端之中;即使不作定性要求,部分學生也能用分數表示可能性的大小。但蘇教版教材對可能性的大小僅限定性描述而不要求定量表示,則是要拉長對隨機性的體驗。因為不管可能性是大是小,一切皆有可能,在于結果的不確定性,學習的難點則在于對隨機性的理解。隨機性至少應該包括兩個方面:(1)單一事件的不確定性和不可預見性;(2)事件在經歷多次重復實驗中所表現出的規律性。看似簡單,認可卻很困難。即使是一些教師,沒有接受隨機思想,在課堂實驗中出現“意外”時,也總是手足無措。
可能性的大小,具體是多少可以緩一緩,過早定量看似進入了更高階的概率學習,實質是縮短了學生對隨機思想理解、內化的過程。讓定性飛一會兒,讓學生親臨隨機環境,親自試驗和收集隨機數據,經歷統計過程,從而豐富對隨機現象的認識,積累大量的活動經驗,體會隨機思想,讓隨機思想煸熟我們的冷飯。
三、指向學科素養——將“冷飯”炒香
數據分析作為數學學科素養的重要方面,在小學數學教學中也有所體現。數據分析觀念包含三類思想:(1)整體思想:從整體上觀察、研究和把握數據;(2)隨機思想:認識不確定性的普遍存在,通過偶然發現必然;(3)相對思想:任何結論都相對于一定的條件,統計的方法沒有對與錯,只有好與不好。《課標(2011版)》將“統計觀念”修改為“數據分析觀念”,增補了對隨機思想的要求:通過數據分析體驗隨機性,一方面,對于同樣的事情,每次收集到的數據可能不同,另一方面,只要有足夠的數據就可能從中發現規律。因此,在可能性的教學中,在實施概率實驗和感悟隨機性的同時,應注重對上述三類思想的滲透,從而提升學生的數據分析素養。
蘇教版教材重視數據的分析和推測,四年級上冊“可能性”單元最后部分的“動手做”,即是由實驗結果推測球的組成的活動。在六年級可能性復習的第4題,則是升級版,將兩色球換成了三種花色的撲克牌。但是,由于同一副牌中每張牌都有區別,所以盡管花色不同,但同花色的撲克牌由于數不同,也有差別,所以看似三類的不同組合,其實是6個單一個體,所以,多次實驗結果后,學生記住出現過的撲克牌,推測反而變得簡單了。于是,復習中還是將撲克牌換成了三種不同的顏色的球共6個,讓學生更多關注實驗的整體數據,而不僅是每次出現的具體情況,通過有限次(30次)的實驗來推測球的組成。
應當說這樣的推測活動非常必要,生活中很多隨機事件,例如,拋瓶蓋和天氣預測,沒有準確的計算結果,只能通過大量的數據得到隨機事件出現的頻率去估計概率,這樣的推測活動具有重要的現實意義。但是,學生的數據分析水平如何呢?筆者進行了上述實驗。
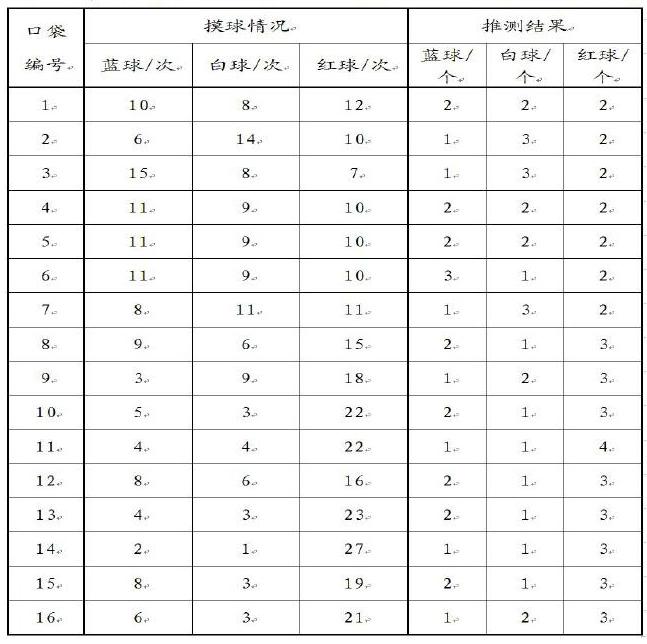
由于課堂時間所限,筆者僅安排了兩類組成,共16組:第1-8組,袋中有籃球2個、白球2個、紅球2個;第9-16組,袋中有籃球1個、白球1個、紅球4個。每組進行30次有放回的摸球,推測袋中球的組成。16組的活動數據如下:
1-8組中推測正確的有3組,占37.5%;9-16組中推測正確的有1組,占12.5%。仔細分析推測錯誤的數據,有摸球結果隨機性導致推測困難的原因,也有數據分析不得法,導致推測錯誤的原因。例如,4、5、6組摸球結果相同,但是第6組卻推測錯誤,是因為使用了相差法,同時也體現了該組同學對隨機性認識不足。從整體16組來看,相對于用比來解釋數據的關系,更多小組傾向于用相差關系分析數據,這也是目前大部分學生的數據分析水平。所以,教學中教師需加強對學生數據分析方法的指導,只有指向學科素養的教學才具有生命力,才能讓這盤冷飯既香又有營養。
縱觀數學史,統計學是一門古老的學問,迄今已有2300多年的歷史,而概率論則是一門新興科學,至今還不到400年。人類的發展尚需孕育這么多年,個體的成長總與歷史相像,所以,“可能性”復習內容雖少尤多,需要教師在教學中更有意識地滲透,幫助學生跨越這漫長的歷史發展過程,更深入地接納概率知識。
【參考文獻】
[1]陳希孺.機會的數學[M].北京:清華大學出版社,2000:60

