正則角聯鎖組織的矩陣模型及其生成算法
王 旭, 杜增鋒, 倪慶清, 劉新華,2
(1. 安徽工程大學 紡織服裝學院, 安徽 蕪湖 241000; 2. 安徽工程大學 紡織科技公共服務平臺, 安徽 蕪湖 241000; 3. 信州大學 纖維學部, 日本 長野 3868567)
三維紡織復合材料增強體結構中角聯鎖組織應用較為廣泛,由于接結紗將多層經、緯紗線固結成整體,增強了經、緯紗線間的聯系,從而提高了抗沖擊和抗分層破壞的能力[1-2]。角聯鎖組織分經紗接結、緯紗接結2種,前者以接結經紗和緯紗交織,后者以接結緯紗和經紗交織。以經紗接結角聯鎖為例,如果只有接結經紗和緯紗2個紗線系統,即為無襯經紗角聯鎖組織。如果在相鄰緯紗層之間還填充有襯經紗,即為有襯經紗角聯鎖組織[3]。楊小俠[4]以5層角聯鎖組織為例,分析了實口、空口及有無襯經紗情況下的組織參數、上機圖設計和上機織造要點。可以看出,和簡單組織相比角聯鎖組織結構和上機圖更加復雜。角聯鎖組織圖是反映交織規律的重要圖解,通常由人工根據交織示意圖進行。由于交織規律復雜,組織圖設計過程效率低、易出錯。如何提高角聯鎖組織的設計效率一直是該領域的研究熱點。許鶴等[5]通過分析角聯鎖組織經紗的浮沉規律并結合角聯鎖經緯紗循環關系,提出一種基于數字排列的角聯鎖組織的設計方法。聶建斌等[6]根據角聯鎖織物的交織規律并結合織物組織參數,提出一種以分式結構來表達交織規律的簡便方法,無需繪制交織示意圖即可根據分式直接得到組織圖。
上述研究為簡化角聯鎖組織交織規律的表達提供了理論參考。近年來研究者開始運用計算機輔助設計提高角聯鎖組織的設計效率。白燕[7]以正則多重緯角聯鎖組織為例,運用組織參數之間的關系并結合Excel工作表,提出了一種快速繪制交織示意圖的方法,通過復制第1經紗交織規律并調整起始點黏貼等方法,實現組織圖的繪制。該方法屬于交互式的操作,仍需要人工參與繪圖過程,其繪圖效率的提高受到一定限制。許璀瑩等[8]研究了實口重緯結構角聯鎖組織的交織規律,并探討了計算機輔助組織圖繪制過程。CHEN等[9]根據角聯鎖組織的交織規律開發了交織示意圖和組織圖的設計程序,通過輸入組織參數,實現了參數化繪圖,提高了繪圖效率。
上述研究表明,建立反映交織規律的織物組織矩陣模型是運用計算機輔助織物組織設計的關鍵環節,目前雖然已有織物組織矩陣模型的報道,但涉及角聯鎖組織矩陣模型的研究尚不多見。本文以經紗接結正則貫穿角聯鎖組織為例,探討無襯經紗和有襯經紗時矩陣模型及其生成算法,并給出無襯經紗矩陣中第1接結經紗列向量和有襯經紗矩陣列向量的賦值算法,為提高該類組織設計效率提供了參考。
1 正則貫穿角聯鎖組織的交織規律
經紗接結角聯鎖組織按交織方式可分為貫穿和層間角聯鎖2種。按照交織規律性,又可分為正則和變則角聯鎖2種。三維紡織復合材料增強體結構中正則貫穿角聯鎖組織應用較多,接結紗以一定的傾斜角貫穿整個織物厚度,與各層緯紗以角聯鎖狀交織,接結經紗間交叉口填入緯紗。根據相鄰兩層緯紗中有無襯經紗,正則貫穿角聯鎖又分為無襯經紗和有襯經紗2種情況,其交織示意圖如圖1所示。
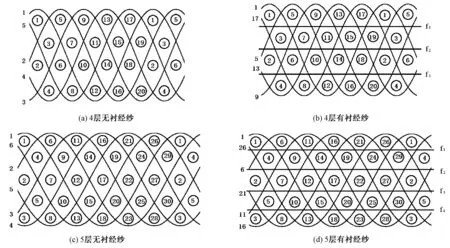
圖1 正則角聯鎖組織交織示意圖Fig.1 Diagram of regular angle-interlock weave. (a) 4 layers no-filling warps; (b) 4 layers with filling warps; (c) 5 layers no-filling warps; (d) 5 layers with filling warps
為便于分析,對圖1中的標記做如下規定:1)圖中圓圈、曲線和水平直線分別表示緯紗、接結經紗和襯經紗;2)每行圓圈代表1層緯紗,圓圈內數字為緯紗序號,從上向下依次編號;3)左側數字代表接結經紗序號,以最上一層緯紗接結經紗從左到右出現順序依次編號;4)右側字符表示襯經紗序號,相鄰2根接結經紗間從上到下相鄰緯紗層間依次填入襯經紗。
正則貫穿角聯鎖的組織圖可根據組織參數確定。分析圖1所示的交織規律可得到如圖2所示的組織圖。圖中緯紗與接結經紗、襯經紗交織處的經組織點分別用“×”“■”表示,交織處的緯組織點均用“□”表示。

圖2 正則角聯鎖組織圖Fig.2 Weave diagram of angle-interlock. (a) 4 layers no-filling warps; (b) 4 layers with filling warps; (c) 5 layers no-filling warps; (d) 5 layers with filling warps
1.1 無襯經紗角聯鎖組織交織規律
圖1(a)示出4層無襯經紗的情況:1個完全組織循環包含5根接結經紗,緯紗4層,每層5根,1個完全組織循環共20根緯紗。圖1(c)示出5層無襯經紗的情況:1個完全組織循環包含6根接結經,緯紗5層,每層6根,1個完全組織循環共30根緯紗。
令緯紗層數、完全組織經紗數、完全組織緯紗數和接結經紗間經向飛數分別為n、RJ、RW和SJ,則由圖1(a)、(c)無襯經紗角聯鎖組織的交織規律,RJ,RW,SJ分別滿足式(1)~(3)。
RJ=n+1
(1)
RW=n×(n+1)
(2)
SJ=n
(3)
圖2(a)、(c)所示的無襯經紗角聯鎖組織圖有如下規律:各接結經紗的交織規律一致;相鄰接結經紗間滿足飛數關系。
1.2 有襯經紗角聯鎖組織交織規律
圖1(b)示出4層有襯經紗的情況:1個完全組織內包含經紗20根,其中5根接結經分別為第1、5、9、13、17根經紗,其余為襯經紗,分5組每組3根(用f1、f2、f3表示),分別位于相鄰接結經紗間的相鄰緯紗層間;緯紗4層,每層5根,1個完全組織循環共20根緯紗。圖1(d)示出5層有襯經紗的情況:1個完全組織內包含經紗30根,其中6根為接結經,分別為第1、6、11、16、21、26根經紗,其余為襯經紗,分6組每組4根(用f1、f2、f3、f4表示),分別位于相鄰接結經紗間的相鄰緯紗層間;緯紗5層,每層6根,1個完全組織循環共30根緯紗。由圖1(b)、(d)有襯經紗角聯鎖組織的交織規律,RJ、RW、SJ分別滿足式(4)~(6)。
RJ=n×(n+1)
(4)
RW=n×(n+1)
(5)
SJ=n
(6)
圖2(b)、(d)所示的有襯經紗角聯鎖組織圖有如下規律:1)各根接結經紗的交織規律一致; 2)相鄰接結經紗間滿足飛數關系;3)一組襯經紗內的各襯經紗的交織規律均不相同,但是每相鄰2根接結經紗之間的各組對應次序的襯經紗交織規律一致。
2 正則角聯鎖矩陣模型及生成算法
根據正則貫穿角聯鎖組織的特點,可構建矩陣A來表達交織規律,見式(7)。矩陣A的行數r、列數c分別為完全組織緯、經紗數,即r=RW、c=RJ。為區別不同的組織點,式(7)中矩陣元素ai,j用不同的符號表示,本文用u、v分別表示接結經紗與緯紗交織形成的經、緯組織點,用g、h分別表示襯經紗與緯紗交織形成的經、緯組織點。
(7)
2.1 無襯經紗角聯鎖矩陣模型及生成算法
根據圖2(a)所示無襯經紗角聯鎖組織交織規律,其矩陣A的列數c=RJ、行數r=RW,分別按式(1)、(2)確定。矩陣A的列向量代表接結經紗,其元素ai,j分別用u、v代表接結經紗的經、緯組織點。
無襯經紗角聯鎖矩陣A的生成算法,實質上是矩陣A中元素ai,j的產生過程。由于1個完全組織循環內接結經紗的交織規律一致,且相鄰接結經紗的經向飛數SJ與緯紗層數n間滿足式(3),因此只需要確定第1接結經紗的交織規律,就能按飛數SJ依次確定其他接結經紗的交織規律,從而完成矩陣A的產生。具體生成算法包括3個步驟。
1)生成第1列接結經紗的交織規律。
第1列接結經紗的交織規律可參照式(8)、(9)的分式表示,其中式(8)表示緯紗層數n為偶數,式(9)表示緯紗層數n為奇數時的交織規律[6]。該方法有利于用計算機程序按列進行矩陣賦值,可提高設計效率。
(8)
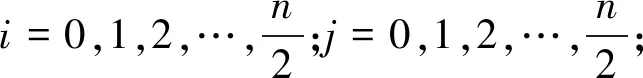
(9)
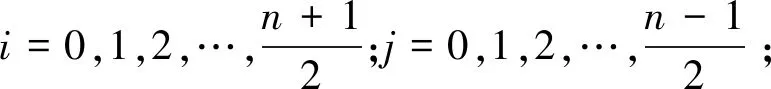
以圖1(c)所示為例,n=5,根據式(9)得出第1接結經紗的交織規律如下:
2)生成矩陣A的第1列向量。
無襯經紗矩陣A的第1列向量的元素ai,1賦值,可根據式(8),或式(9),從左到右依次從分子b、分母d取值,當從分子b取值時,ai,1取u,當從分母d取值時,ai,1取v,其滿足式(10)。
(10)
式中:b、d的下角標x=0時,令b0=0,d0=0;i=1,2,…,r。
以第1對分子分母為例,當0 3)生成矩陣A的其他列向量。 矩陣A的第2至c列,則按相鄰列間的飛數SJ關系[10],運用式(11)逐列進行賦值。 (11) 式中:下標i,j分別為矩陣元素的行序、列序;i=1,2,…,r;j=2,3,…,c;SJ為經向飛數;RW為完全組織緯紗數。 由式(11)可知第j列向量可由第j-1列向量向上移動SJ得到。當滿足i+SJ≤RW,則將j-1列第i+SJ行元素都賦值給第j列第i行。當滿足i+SJ>RW,則將j-1列第i+SJ-RW行元素都賦值給第j列第i行。以此類推完成矩陣A的全部元素賦值。 對比圖2(b)和圖2(a)、圖2(d)和圖2(c)發現,有襯經紗和無襯經紗,在緯紗層數n相同時,接結經紗與緯紗的交織規律完全一致。有襯經紗相當于在無襯經紗的基礎上,相鄰接結經紗間嵌入1組襯經紗與緯紗交織構成。令n層緯紗有襯經紗角聯鎖組織矩陣為A,其列數c、行數r分別為SJ、RW,可按式(4)、(5)確定。整個矩陣A可看成由接結經紗矩陣A1和襯經紗矩陣A2組合構成。其中矩陣A1分別用元素u、v代表接結經與緯紗交織形成的經、緯組織點。矩陣A2分別用元素g、h代表襯經紗與緯紗交織形成的經、緯組織點。矩陣A1的行數r1=n(n+1),列數c1=n+1。矩陣A2的行數r2=n(n+1)、列數c2=n-1。 矩陣A可由矩陣A1的列向量之間分別嵌入矩陣A2構成,具體生成算法分3個步驟。 1)生成接結經紗矩陣A1。矩陣A1可根據2.1節建立。 2)生成襯經紗矩陣A2。根據圖2(b)、(d)的交織規律,矩陣A2可先將第1列,按式(12)進行賦值,然后第2列在第1列的基礎上按式(13)賦值,以此類推,后一列在前一列的基礎上,奇數列按式(12)賦值,偶數列按式(13)賦值,最終得到矩陣A2。 (12) 式中:k=1,2,…;j=1,3,5,…。 (13) 式中:int為截尾取整計算;k=1,2,…;j=2,4,6,…。 3)生成有襯經紗角聯鎖矩陣A。根據接結經紗矩陣A1和襯經紗矩陣A2,按照式(14)相互嵌入,建立矩陣A: (14) 式中:A(:,j)為矩陣A第j列向量;A1(:,l)為矩陣A1第l列向量,l=1,2,…,c1;A2(:,m)為矩陣A2第m列向量,m=1,2,…,c2。 以圖2(b)所示為例,驗證矩陣A的生成算法。 由層數n=4,根據式(4)~(6),得到RJ=20,RW=20,SJ=4,則矩陣列數c1=20,行數r1=20。n為偶數緯紗層數,首先按式(8)得到第1接結經紗交織規律: 根據第1經紗交織規律,由式(10)依次帶入i=1,2,…,r1得到矩陣A1的第1列向量ai,1。再由式(11),依次帶入j=2,3,4,5,得到矩陣A1的第2至第5列向量,ai,2,ai,3,ai,4,ai,5,如圖3所示。 由2.2節可知,層數n=4,襯經紗矩陣A2的行數r2=20,列數c2=3。矩陣A2的奇數列、偶數列分別由式(12)、(13)得到。按照式(12),帶入j=1可得出ai,1在i為1、5、9、13、17時取h,其他位置時取g。將ai,1賦值給ai,2,按照式(13),帶入j=2可得出ai,2在i為3、7、11、15、19時取h。將ai,2賦值給ai,3,按照式(12),帶入j=3可得出ai,3在i為2、6、10、14、18時取h。最終得到圖3所示的襯經紗矩陣A2。 如圖3所示,先將接結經紗矩陣A1放入矩陣A。由式(14)可知,n=4,l分別帶入1、2、3、4、5時,j分別為1,5,9,13,17,即矩陣A的第1、5、9、13、17列分別等于矩陣A1的第1、2、3、4、5列。再將襯經紗矩陣A2放入矩陣A。由式(14)可知:當n=4,l=1時,m分別取1、2、3,得到j分別為2,3,4,即矩陣A2的第1、2、3列分別賦值給矩陣A的第2、3、4列;當n=4,l=2時,m分別取1、2、3時,得到j分別為6、7、8,即矩陣A2的第1、2、3列分別賦值給矩陣A的第6、7、8列。重復上述過程,可產生矩陣A的所有列。 圖3 4層有襯經紗正則角聯鎖組織矩陣 上述驗證表明,本文給出的正則貫穿角聯鎖組織矩陣生成算法是正確的。 本文以經紗接結正則貫穿角聯鎖組織為例建立了:1)無襯經紗和有襯經紗正則貫穿角聯鎖組織矩陣模型;2)提出了無襯經紗正則貫穿角聯鎖組織矩陣中第1接結經紗列向量的賦值算法,并給出利用飛數關系的矩陣生成算法,通過輸入緯紗層數即可根據上述算法產生對應的組織矩陣;3)提出了有襯經紗正則貫穿角聯鎖組織矩陣中襯經紗矩陣列向量的賦值算法,并給出通過接結經紗矩陣和襯經紗矩陣嵌入的矩陣生成算法,通過輸入緯紗層數即可根據上述算法產生對應的組織矩陣。 FZXB2.2 有襯經紗角聯鎖矩陣模型及生成算法
3 矩陣生成算法驗證
3.1 接結經紗矩陣A1生成
3.2 襯經紗矩陣A2生成
3.3 有襯經紗角聯鎖矩陣A生成
Fig.3 Weave matrix of four layers regular angle-interlock with filling warps4 結束語

