基于S變換的高速列車小幅蛇行識別方法

寧 靜 冉 偉 種傳杰 陳春俊

西南交通大學機械工程學院，成都，610036

0 引言

高速列車運行過程中的橫向穩定性至關重要。由于列車輪對具有一定的錐度，因此即使車輛沿平直的軌道運行，只要有一個初始激勵，輪對就會繞軌道中心線一邊橫移一邊搖頭向前耦合運動，即產生蛇行運動[1]。若車輛以較高的速度運行，則當蛇行運動頻率與車輛自振頻率接近時，其振幅不斷擴大，這時的蛇行運動就喪失了穩定性，即發生了蛇行失穩，且幅值增大越快，失穩的程度就越嚴重。

在列車實際運行過程中，基于軌道不平順和車輪磨損等原因，當列車速度小于蛇行失穩理論臨界速度時，就有可能發生失穩現象[2]。筆者在對某型高速列車的在線跟蹤試驗數據進行分析時發現[3]，列車在時速超過300 km/h運行時易出現小幅蛇行運動，且有的小幅蛇行出現后會緊接著出現蛇行異常。考慮到小幅蛇行可能會導致蛇行異常，因此，非常有必要對小幅蛇行進行監測，進而及早采取措施消除小幅蛇行，以保證高速列車的安全運行。

國內針對小幅蛇行的監測進行了一些研究。蔡里軍[2]認為，轉向架橫向振動加速度峰值出現連續6次以上達到或者超過極限值2 m/s2(現有標準為8～10 m/s2)且符合相關條件時，在工程上即可判定轉向架發生蛇行運動失穩，但此判據是完全依據多次蛇行異常的在線測試數據以及工程實踐經驗得出的，沒有對小幅蛇行現象進行相關的理論研究，此結論是否具有普遍意義，還需要進一步探討與驗證。孫麗霞[4]從提高車輛橫向穩定性安全裕量的角度，通過計算高速列車轉向架構架橫向振動加速度均方根值，提出了一種監測轉向架小振幅蛇行振動的方法。但此類方法對監測數據采取的數據處理方法都是基于平穩數據的，沒有考慮高速列車振動信號的非平穩特性。

高速列車的橫向穩定性系統特征具有很強的非平穩和非線性特征，可以認為列車在線監測數據的本質為時變系統在非平穩激勵作用下的非平穩、非線性、多信號的輸出，因此，使用傳統的平穩信號處理方式研究高速列車的蛇行運動相關問題顯然是不合適的。考慮到通過現有的跟蹤監測設備[5]能夠方便地獲得高速列車運行時的轉向架橫向加速度信號，本文使用基于時頻分析的信號處理方法提取列車小幅蛇行特征，從而預測蛇行運動，保障列車運行安全。S變換[6]是基于小波變換和短時傅里葉變換的一種時頻分析方法，它結合了短時傅里葉變換(short-time Fourier transform, STFT)和小波變換(wavelet transform)的優點，并且具有相位信息。

本文提出利用S變換對高速列車轉向架橫向加速度信號進行特征提取，對經過S變換得到的復時頻矩陣進一步取模得到模時頻矩陣，提取模時頻矩陣最大能量對應頻率處的時間-幅值特征函數Vf(t)，然后對此特征函數提取4種簡單的特征指標，最后采用最小二乘支持向量機(least square support vector machine, LS-SVM)識別出正常、小幅蛇行以及蛇行異常3種不同的運行狀態。

1 試驗數據

經跟蹤觀察，某型高速列車在某線路運行的過程中易出現蛇行異常振動。針對此情況， 2011年3月12日至2011年4月20日期間對運行在該區間的列車進行了專門的跟蹤試驗[7]。本次試驗在轉向架上安裝了加速度傳感器，加速度傳感器的型號為LC0709A-18，量程為(-18～18)g，速度信息通過GPS系統采集。

對跟蹤試驗數據進行分析時發現，當列車運行速度在340 km/h左右且未見明顯增大的情況下，某型高速列車的轉向架橫向加速度信號還易出現幅值較小的極限環——小幅蛇行現象。在這種情況下，轉向架橫向加速度信號幅值會慢慢變大，列車運行因此會經歷從正常運行到小幅蛇行，最后發散到蛇行異常的過程，如圖1所示。

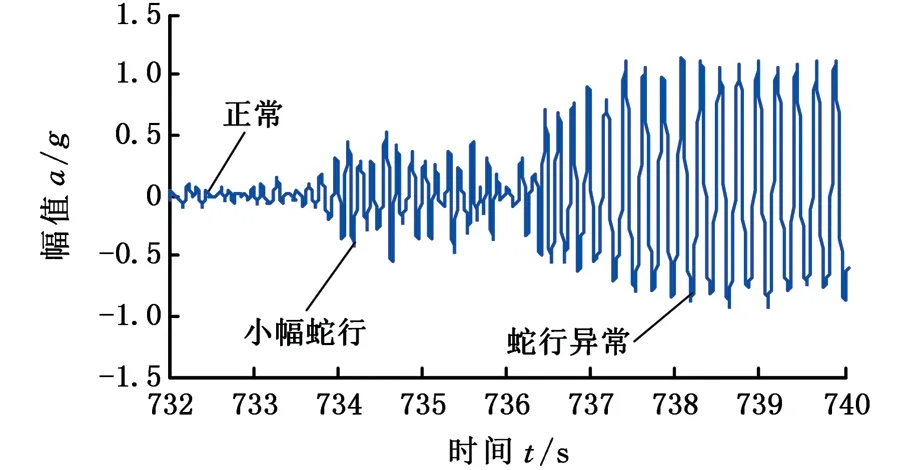
圖1 一段產生蛇行運動的轉向架構架橫向加速度和速度數據Fig.1 A section of the hunting movement of the bogie frame lateral acceleration and speed

為研究如何準確識別轉向架小幅蛇行，對采集到的原始信號進行分類截取。對蛇行異常振動嚴格按照轉向架構架橫向加速度幅值連續6次大于8 m/s2進行截取，橫向加速度幅值小于2 m/s2即為正常運行狀態，高速列車小幅蛇行數據則是加速度幅值介于2～8 m/s2之間的數據。本文對此三種狀態下的轉向架橫向加速度信號分別選取36組樣本數據，將每種狀態下的36組樣本數據進行歸一化后，將其均分成兩部分，18組作為訓練樣本，另18組數據作為測試樣本。

考慮到在線試驗成本較高，測試數據不僅用于蛇行運動分析，還可用于研究高速列車的振動演變規律研究等，設置本次試驗的采樣頻率為2 500 Hz。由于蛇行運動本身是低頻振動，為便于進行數據處理，結合香農采樣定理，對數據進行250 Hz的重采樣，然后進行2～12.07 Hz的帶通濾波。關于數據長度的選取，考慮到樣本數據過短會導致信息不完整，而樣本數據過長會導致采樣和計算時間增加，不利于預測和后面的控制操作。通過對大量數據觀察發現，取數據段的時間長度t=2 s是符合實際情況的，2 s的數據段包含了故障狀態主要時頻特征，同時數據長度相對較短。因此，結合實際情況，選取250 Hz重采樣后樣本長度為500個的數據點(t=2 s)。

2 當前小幅蛇行監測方法

2.1 當前小幅蛇行監測理論

目前國內外對鐵道客車橫向運動穩定性的評定標準并未統一，相關標準中，關于監測小幅蛇行狀態的評價標準均未涉及。我國鐵道客車行車安全監測標準[8-9]采用的是橫向加速度峰值評價法：當轉向架橫向加速度的峰值連續6次以上(含6次)達到或超過極限值8 m/s2時，則判定轉向架橫向失穩。而國外的相關評定標準[10-13]分別規定：車輛在運行過程中的輪軌橫向力、輪軸橫向力、轉向架橫向加速度及車體橫向加速度不能超過規定限值，否則應減速運行，以保證列車運行的安全。例如歐盟采用的是橫向加速度均方根評價法。歐盟標準的具體做法是將采集到的轉向架橫向加速度數據進行f0±2 Hz的帶通濾波(f0為轉向架的蛇行失穩頻率)，并在整個判定流程中設定步長為10 m，進而計算其長度為100 m的移動均方根值RMS，若此計算結果超過限值y，則判定轉向架失穩，即列車出現蛇行運動。在上述判據中限值y并不唯一，而是根據車輛的轉向架質量來確定，其具體的計算公式可表示為

(1)

其中，mb為轉向架質量(單位為t)，判定限值y的單位為m/s2。

文獻[4]在歐盟標準的基礎上提出了一種識別小幅蛇行的監測方法。首先通過頻譜分析，確定監測信號的強迫振動頻率范圍[fF0,fF1]和監測信號的蛇行振動頻率范圍[fH0,fH1]，然后計算RF和RH。其中，RF為轉向架橫向加速度在強迫振動頻率范圍[fF0,fF1]內的均方根值，RH為轉向架橫向加速度在蛇行振動頻率范圍[fH0,fH1]內的均方根值。RF和RH的計算長度均為100 m，步長為10 m。最后，根據下式判定高速列車的運行狀態

(2)

一旦RF和RH都滿足式(2)中的條件，則判定列車出現小幅蛇行現象。其中，α、β為閾值折減系數。與y的取值相似，閾值折減系數α和β的取值受到車輛結構和軌道不平順的影響。式(2)可進一步表示為

(3)

此外，在上述計算過程中，[fF0,fF1]和[fH0,fH1]的取值隨著車型與線路情況的變化而變化，具體的取值情況應視轉向架實際的強迫振動能量和自激振動能量的主頻分布范圍而定。

2.2 當前小幅蛇行監測理論的局限性

為檢驗現有小幅蛇行監測理論的有效性，本文利用某型車的實測跟蹤數據進行驗證。通過對監測數據進行頻譜分析可知，該型車輛轉向架橫向加速度相關頻率范圍為[fF0,fF1]=[7,12]Hz及[fH0,fH1]=[4,7]Hz。已知該車型動力轉向架質量mb為10 t，即根據式(3)可知，該車型在其運行軌道條件下，若同時滿足RF≤5α和RH>5β即可判定車輛出現小幅蛇行現象。分別選取20組正常和20組小幅蛇行振動信號計算RF和RH值，計算結果如圖2所示。由圖2可發現，小幅蛇行和正常運行兩類信號的RF值在2、6、12樣本組處出現了交集(圖2a)；小幅蛇行和正常運行兩類信號的RH值在2、10、11、13、16、17、18樣本組處出現了交集(圖2b)。這會導致無論如何調整α和β值，都無法把小幅蛇行和正常運行兩類信號區分開來。由此可見，文獻[4]提出的基于均方根值的監測方法大部分情況下能夠實現對小幅蛇行的識別，但個別情況下則無法將小幅蛇行與正常狀態區別開來，從而難以達到對小幅蛇行振蕩進行有效監測的目的。這可能與文獻[4]中，對監測數據采用的數據處理方法都是基于平穩數據的，忽略了高速列車在運行中的非平穩特性有關。

(a)RF值

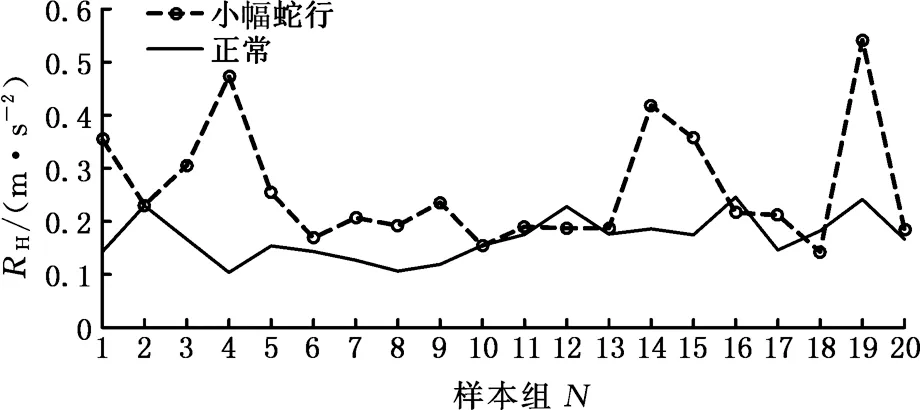
(b)RH值 圖2 20組樣本的RF和RH值Fig.2 RF and RH of the 20 groups of sample data

3 S變換方法

3.1 S變換方法原理

S變換是由STOCKWELL等[14]于1996年首先提出的，它是一種時頻可逆分析方法，具有多分辨率分析的能力，又兼具單頻率獨立分析的特點。S變換可看成是小波變換的“相位修正”，也可從STFT演變而來，信號h(t)的S變換定義為

S(τ,f)=

(4)

式中，t為時間；j為虛數單位；f為頻率；τ為高斯窗函數的中心位置。

由式(4)可以看出，S變換中高斯窗的寬度和高度隨頻率變化而變化，這樣S變換就克服了STFT窗口寬度和高度固定不變的缺陷。

S變換也可寫成兩個函數的卷積：

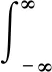
(5)

p(τ,f)=h(τ)exp(-j2πfτ)

(6)

(7)

設B(α,f)為S(τ,f)的傅里葉變換(從τ到α)，由卷積定理可得

B(α,f)=P(α,f)G(α,f)

(8)

其中，P(α,f)、G(α,f)分別為p(τ,f)與g(τ,f)的傅里葉變換，顯然

(9)

其中，H(α+f)是式(6)中的傅里葉變換，指數項是式(7)中的傅里葉變換。因此，S變換可由式(9)的傅里葉逆變換求得(由α到τ)：

(10)

故S變換可利用快速傅里葉變換實現快速計算。

令τ→iT，f→n/(NT) (N為采樣點總數，T為采樣周期)，將信號離散化后可得離散時間序列h(kt)，其中k=0,1,…,N-1，則根據式(10)可得到S變換的離散形式為

n≠0

(11)

其中，i、m、n均為從0～N-1的正整數。

h(kT)為S變換的逆變換，即

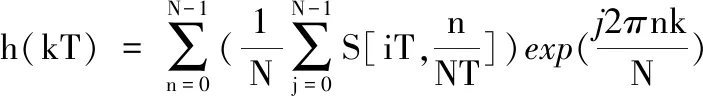
(12)

3.2 S變換處理結果及分析

以高速列車轉向架橫向加速度實測數據為分析對象，每組樣本數據經S變換后得到一復時頻矩陣S[lT,n/(NT)]，其中l表示采樣時刻，其行向量反映了轉向架橫向加速度信號某一時刻的頻率分布，而列向量則反映了轉向架橫向加速度信號某一頻率隨時間變化的情況。對復時頻矩陣S[lT,n/NT]中的元素分別求模后得到S變換模時頻矩陣Sa[lT,n/(NT)]，其表達式如下：

(13)

Sa[lT,n/(NT)] 包含了不同時間點處該矩陣在不同頻率段上幅值的分布情況。

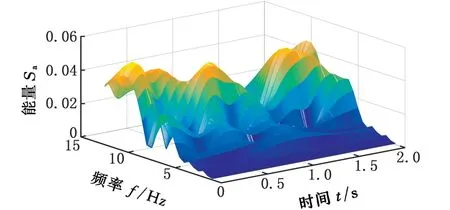
(a)正常

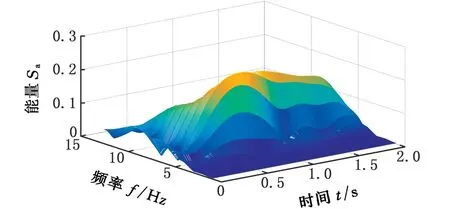
(b)小幅蛇行

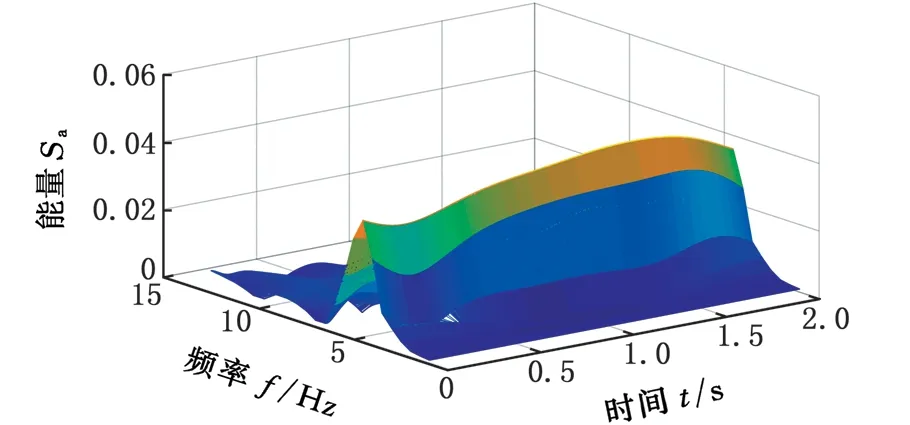
(c)蛇行異常圖3 S變換后的模時頻矩陣Fig.3 The module time-frequency matrix after S-transform

圖3為高速列車分別在3 種狀態(正常、小幅蛇行、蛇行異常)下的監測數據通過S變換后得到的一組模時頻矩陣圖。由圖3a可以看出，當高速列車正常運行時，信號模時頻矩陣的能量Sa在整個時頻域范圍內分布比較分散，且隨著時間的推移，其頻率成分的變化非常明顯。但是總體來看，沒有哪個頻率成分是絕對的主導。由此也可從一個側面說明列車在高速運行狀態下，其振動信號是典型復雜的多分量、非平穩隨機信號。鑒于以上分析，對高速列車的蛇行狀態監測，必須考慮其振動信號的非平穩特性。由圖3c可以看出，在蛇行異常狀態下，信號模時頻矩陣的頻率成分隨時間推移，其幅值變化不大，未見幅值明顯發散的情況，監測信號總體上趨于平穩。這是由于當高速列車處于臨界蛇行狀態時，抗蛇行阻尼器阻礙了蛇行運動的進一步發散，避免了系統的進一步失穩，因此，在監測時間內，表現為系統極限環上的臨界穩定的運動形式。此時，信號的頻率特征較為明顯，其主要能量集中在7 Hz左右，與蛇行運動的基本理論是相符的。圖3b是高速列車處于正常和蛇行失穩之間即小幅蛇行狀態時的信號模時頻矩陣分布圖。由圖3b可以看出，此時的能量分布同樣比較分散，但相對正常狀態似乎在朝某個方向逐漸集中，峰值的頻率成分明顯右移，應該略大于蛇行異常時的主要頻率。從系統角度分析，小幅蛇行是列車系統從一個穩定的平衡解狀態(正常狀態)轉變為另一個穩定的周期解狀態(臨界失穩狀態)過程中的一個系統轉變過程。而圖3b正是這種轉變過程的具體表現，其模時頻分布特征介于正常運行和蛇行異常振動信號的模時頻分布特征之間，是一個逐漸從能量分散的非平穩信號到能量集中的基本平穩的信號轉變過程。

3.3 最大時變特征函數的特征量提取

由圖3分析可得，能量分布的不同是不同狀態下模時頻分布矩陣的最直觀的區別，因此，選取該模時頻分布矩陣中振動能量最為集中的頻率點，對該模時頻分布矩陣進行截取，即可快速構建一個簡單的特征函數，從而將小幅蛇行運動識別出來。

定義能量最大處的時變特征函數為Vf(t)，其表達式為

Vf=Sa(t,fb)

(14)

式中,t為采樣時刻；fb為能量最高處的頻率值。

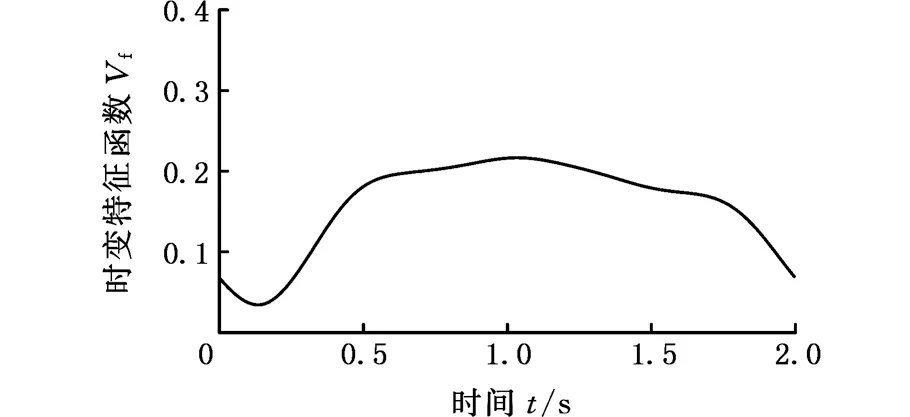
以圖3所示的振動信號為例，求得相應的最大時變特征函數Vf(t)如圖4所示。由圖4可以看出，通過S變換后，3種狀態的模時頻矩陣能量分布差別很大。因此只需簡單地提取模時頻矩陣中的能量最大處的時變特征函數，并提取相關的統計特征指標，即可較好地實現狀態分類。現對得到的模時頻矩陣幅值時變特征函數在整個時間段上提取4個特征指標，分別為最大值(max)、最小值(min)、標準差(mean)、標準差值(std)。

根據對轉向架橫向振動信號最大能量對應的頻率，確定模時頻矩陣幅值時變特征函數Vf(t)，對圖4中的函數分別進行特征指標的提取，經歸一化后，其特征指標如表1所示。

4 S變換方法結果對比分析

為驗證S變換的有效性，本文采用小波變換方法進行對比研究。參照文獻[15]，小波基選為db2，小波分解設為四層，對小波分解最終的近似部分和四個細節部分的小波系數分別進行特征提取，提取的特征指標與Vf(t)提取的特征指標相同，分別為：小波系數的最大值、最小值、均值和標準差。表2所示為小波變換后對小波系數提取的一組特征指標。

為檢驗S變換特征提取方法對小幅蛇行的識別效果，將每種狀態(正常、小幅蛇行、以及蛇行異常)的36組樣本數據均分成兩部分，18組作為訓練樣本，另外18組作為測試樣本，采用LS-SVM來對高速列車的3種不同運行狀態進行識別。LS-SVM分類過程中核函數為高斯核函數，設定懲罰因子c=2，核函數高度控制參數σ=0.2。在對支持向量機進行訓練前，提取的三種狀態的各類特征量指標需進行歸一化處理，以保證所有的特征指標值都介于0～1之間。

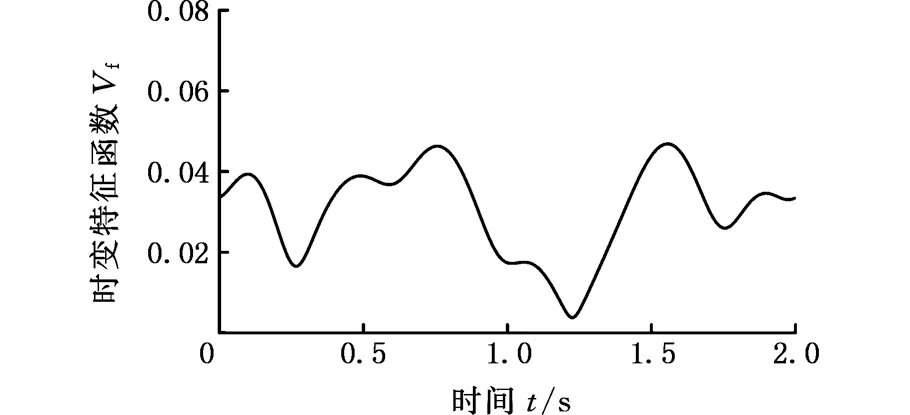
(a)正常

(b)小幅蛇行

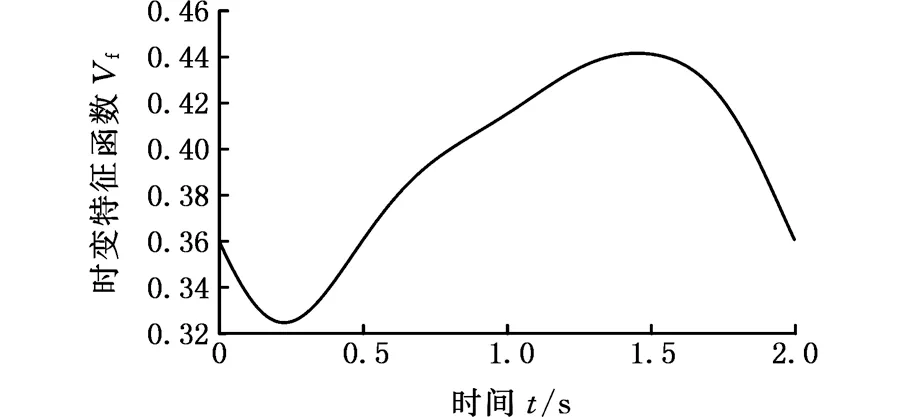
(c)蛇行異常圖4 模時頻矩陣中的能量最大處的時變特征函數Fig.4 The time-amplitude function at the maximum energy frequency point

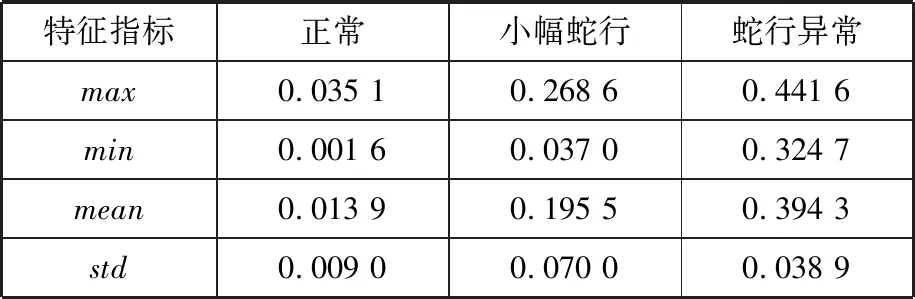
特征指標正常小幅蛇行蛇行異常max0.035 10.268 60.441 6min0.001 60.037 00.324 7mean0.013 90.195 50.394 3std0.009 00.070 00.038 9

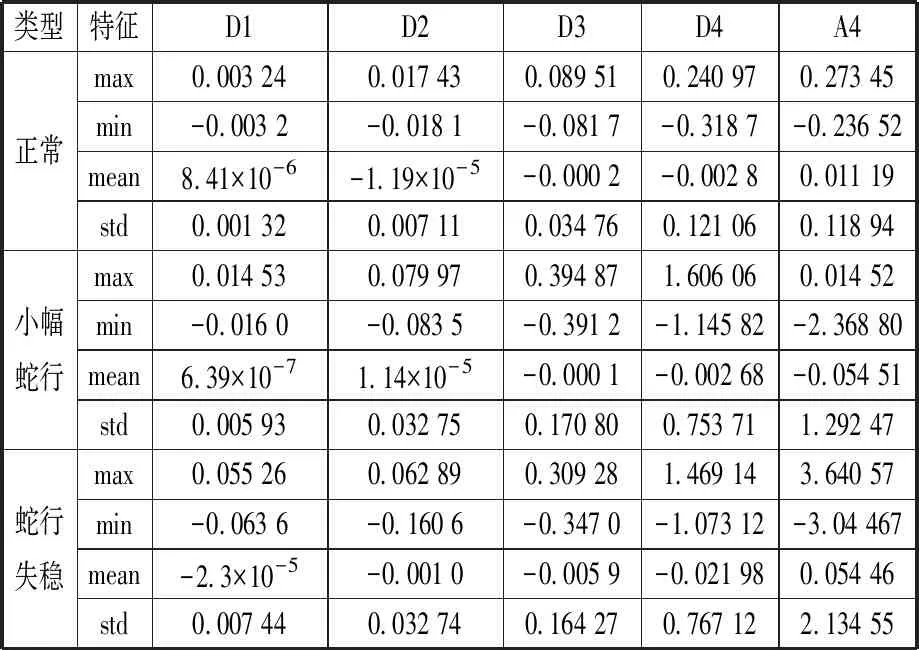
表2 利用小波系數提取的特征指標

S變換特征指標和小波變換特征指標的分類識別結果如表3所示。由表3可以看出利用小波變換后的小波系數提取信號的時頻特征，小波分解能把大部分狀態區分開來，但是小波變換方法本身窗寬為固定值，且窗函數的選擇對分析結果也有較大影響，導致其識別結果并不理想。采用S 變換后，由于S 變換采用高斯窗函數，并且設定窗寬與頻率的倒數成正比，改善了小波變換窗寬固定的缺陷；同時，與小波變換相比，其時頻分布中各頻率分量的相位譜與原始信號保持直接的聯系；此外， 經過S 變換提取的特征量對強噪聲不敏感，從而使得同樣的原始數據，基于S變換的時頻特征提取以及識別結果明顯優于小波變換識別結果。主要表現在兩個方面：對于小幅蛇行的識別采用S變換特征指標的識別率要明顯高于小波變換的特征指標的識別率；與此同時，對于每一組樣本，S變換特征指標只有4個，小波變換的特征指標卻有20個，S變換的特征指標個數要明顯少于小波變換特征指標的個數。

表3 支持向量機識別結果對比

5 結語

小波變換是經典的非平穩信號的處理方法，其分辨率可調，廣泛應用于非平穩信號特征提取當中，然而，小波變換窗寬為固定值，且窗函數的選擇對分析結果也有較大影響，致使其對高速列車小幅蛇行識別效果并不理想。

高速列車轉向架橫向加速度信號具有非線性、非平穩的特點，傳統的特征提取方法不能有效地提取信號特征。本文提出基于S變換的高速列車小幅蛇行特征提取方法，實現了對小幅蛇行的準確識別，并能對蛇行異常產生一定的預警作用。識別結果表明，基于S變換的時頻特征提取方法優于基于小波變換的時頻特征提取方法。

以上研究完全依據多次蛇行異常的在線實際監測數據，但是由于試驗條件限制，現場采集的蛇行異常數據非常有限，目前分析的小幅蛇行信號僅僅來源于某次蛇行異常的在線測試數據，此次特征提取方法是否具有普遍意義，還需要進一步對小幅蛇行的演變機理進行研究。