讓數學課堂因生成而精彩

陳錦鳳

[摘 ?要] 新課改風向標下，初中數學課堂教學應該是預設與生成的同構共建，融為一體. 富有生成的課堂是具有生命力的，可以發揮學生的主體地位，充分展現教師的教學機智和教學藝術，讓學生探究知識的欲望得以實現，讓課堂教學更真實、更精彩. 文章結合教學實踐，從“充分預設，期待精彩;拋磚引玉，孕育生成;巧借錯誤，促進生成;精心篩選，升華生成”等幾個方面作了探討.

[關鍵詞] 初中數學課堂;預設;思考;探究;動態生成

傳統的教學模式中循規蹈矩，課堂缺少生機和趣味，透出的是枯燥和乏味，而新課程理念所追求的是理想的具有“動態生成”的課堂模式. 課堂應是開放的、生動的、互動的、多維的，是充滿生命活力的、具有智慧和挑戰的課堂. 只有在這樣的課堂教學中，教師的設想才能產生有效生成，才能讓數學課堂因生成而精彩[1]. 那么，如何在教學實踐探究中駕馭這種生成呢？本文中筆者選取了具有典型意義和探究價值的教學案例進行分析.

充分預設，期待精彩

課堂的有效生成是預設的生長和形成，是預設的思路和設想在教學情境中的自然生長. 凡事預則立，不預則廢. 在課前教師需深入探究教材，對學生的興趣點和興奮點作一定的了解，巧妙運用文本信息，設計和分配問題. 在教師設計教學方案和問題的過程中，需仔細研究課程標準，鉆研教材，估計學生已有的知識技能和直接經驗，讓學生的智慧之花綻放，等待生成[2]. 教師看似守著預設，放手學生的主動發揮，而實則是教師宏觀把控.

不少教育專家都對教師的備課提出了“三個吃透”原則，即“吃透”課標，“吃透”教材，“吃透”學生. 不過，應該沒有一個教師可以完全做到這“三個吃透”原則，甚至于其中的一項“吃透”都很難達成. 而我們可以將其視為教學中長久的追求目標，竭盡所能充分預設，做到胸有成竹，才能在課堂上做到游刃有余，才能在應對學生的各種生成時做到臨陣不慌.

案例1：在探究“一次函數的圖像”時，筆者引入了以下這道例題：

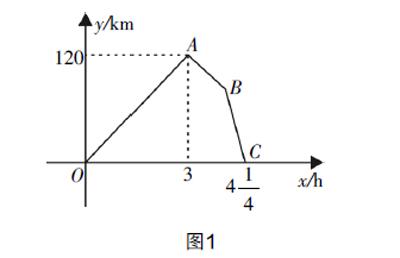
某普通客車和快車同時以各自的車速勻速從甲城開往乙城，快車到達乙城后下客和等待上客一共用去了45分鐘，又立刻由原路以另一速度勻速返回，直至與普通客車相遇. 已知普通客車的速度為60 km/h，兩個車之間的距離y（km）與普通客車行駛時間x（h）之間的函數圖像如圖1所示，有以下四個結論：①快車從甲城到乙城的速度為100 km/h;②甲城到乙城的距離為120 km;③圖1中點B的坐標是（3.75，75）;④快車從乙城返回的速度為90 km/h. 其中正確的結論是________.（請填上正確結論的序號）

此案例的正確答案為①③④.

筆者在設計時充分預設了學生的解答結果：第一種情況，一些學生在審題時會出現不夠仔細的情況，讀圖不仔細或是不理解，這樣一來自然就無從下手了;第二種情況，一些學生會存在理解上的偏差，認為結論②也是正確的;第三種情況，一小部分學生能仔細審題并做到準確解決.

同時，筆者還充分預設了課堂中的學習方法：首先忽略后三個結論，著重鑒定結論①是否正確. 將所持結論相左的學生分為兩組進行辯論，其余學生作為裁判;得到結果后，再分小組討論后三個結論的正確性;最后每個小組派一名學生陳述結果的同時闡明理由.

由此可見，充分的預設加以精心捕捉知識的生成點，有利于學生思維空間的延展，有助于學生想象力和創造力的釋放，讓學生自帶知識、經驗、思考和興致參與課堂教學. 只有在這樣的預設下，精彩才能不期而會.

拋磚引玉，孕育生成

在課堂教學中，想要預設的生成點如花朵般燦爛，還需要通過一些問題的設計，打開學生思維的空間，讓學生談一談看法，說一說依據，釋放學生的想象力和創造力，使學生快速興奮起來，積極有效地進行創造性的思維和表達，有效地推進學生智力和思維水平的提升.

案例2：在引領學生探究“概率”這一內容時，筆者設計了問題“拋擲硬幣出現正反面可能性的概括”. 首先，探究“拋擲一枚硬幣出現正反面的概率”，學生經過思考很快得出了答案 . 筆者拾級而上，問道“當同時拋擲兩枚硬幣時，出現一正一反的概率為多少呢？”這一提問極大地激發了學生的興趣和思考，學生的思維被激活了，各抒己見，幾種不同的意見隨即誕生了. 筆者沒有將結論直接拋給學生，而是讓學生自己去思考和解決. 讓筆者欣喜的是，下課鈴響了，學生們還是意猶未盡，還在思考著、討論著、爭辯著……

巧借錯誤，促進生成

在課堂教學中，教師可以巧借學生知識理解的認知偏差和失誤，設計一些錯誤的結論，或是誘導學生犯錯的問題，這是鮮活的課程資源. 教師需善待這些生成性資源，并讓學生經歷辯論、討論和探究這一系列過程，從中吸取教訓，實現資源的再創造，讓“錯誤”促進生成.

案例3：在教學“分式的基本性質”中，學生由于剛剛接觸分式的約分，對其知識梳理得還不夠清晰，以下是兩名學生所做的兩種變形方法：

生1： = =x-y.

生2： = =x-y.

師：他們的做法都正確嗎？

（學生們各執一詞，互相辯論）

師：請各自講一講你們的不同看法，并說明原因.

生3：結果都是一樣，都是對的.

生4：不對，盡管結果都是一樣的，但生2的過程是錯誤的.

師：（追問）過程中哪里有錯呢？

生4：他將分子和分母同時乘以x-y，如果x-y=0呢？很顯然，這就不滿足“分式的分子和分母同時乘的整式不能為0”，因此他是錯誤的.

師：說得非常好，在學習分式的性質時，這一前提條件是非常重要的，不能遺漏.

……

這樣一來，教師及時抓住了學生的錯誤，在點撥和誘導下，學生主動探究、發現并解決了這一錯誤，不僅使學生逐步深化了分式的性質，也使學生在探究過程中感悟到數學的無窮樂趣. 當然，這里的生成性資源的產生也提醒著教師，在“分式的基礎性質”這一內容的學習中學生仍存在著一定的問題，需強化好這一前提條件，才能為后續問題的解決做好鋪墊.

案例4：在學習“完全平方公式”前，筆者出示了以下等式：（1）（ab）2=a2b2;（2）（a+b）2=a2+b2;（3）（a-b）2=a2-b2. 然后拋出以下“問題串”，引領學生的思維：這三個等式都正確嗎？你是如何判別它們是否正確的？若不正確，該如何修改呢？……通過“問題串”的引導，一方面有助于糾正學生的錯誤，加深對知識的理解;另一方面可以搭建學生思維創造性和靈活性的形成路徑.

精心篩選，升華生成

課堂生成的實際情況千變萬化，面對豐富多彩的生成性資源，教師不可能在有限的教學時間內發揮殆盡. 因此，需進行靈活篩選，或激發學生的認知沖突，或延展教學內容，或引申問題，學會做生成信息的剪裁者和動態生成的催發者，以自身的教學機智進行引導，使課堂創生出精彩.

首先，需創設符合數學課程目標的有效生成. 教師可以依據長期、中期和近期目標適當地進行刪除、增補、提升，來促進學生的有效學習. 其次，生成需在大部分學生所能接受的范圍內. 篩選的內容以大部分學生的知識經驗為基礎，需要兼顧多數學生，而不僅僅是少數學優生的舞臺. 最后，篩選的生成性資源需具有價值性，需選擇一些具有一定價值的問題進行點撥和引導，促進有效生成.

總之，新課程需要一個生成性的課堂，教師需要不斷提高自己的教學能力和業務水平，充分培養教學機智. 在教學中，樹立“以生為本，以學定教”的教學思想，在課前做好充足的備課準備，研究課標、教材、學生、教法等，進行精心預設;在課中盡可能地超越預設，把握課堂中的閃光之處，追求動態生成，讓課堂在預設與生成的完美融合中綻放光彩[3].

參考文獻：

[1] 黃廣志. 淺談技校數學教學生活化的策略[J]. 數學學習與研究，2012（13）.

[2] 溫建紅. 論數學課堂預設提問的策略[J]. 數學教育學報，2011，20（03）.

[3] 卓寶才. 讓動態生成隨著課程資源開發動起來[J]. 考試周刊，2008（38）.