對一道函數綜合題的突破與反思

張維茂

[摘 ?要] 二次函數是初中數學的重點知識，以其為基礎命制的綜合題也是歷年中考的壓軸題，該類考題的破解需要充分把握問題特征，利用關聯知識和相應的策略對問題簡化突破. 文章以一道函數與幾何綜合題為例，開展思路突破和解后反思，提出相應的教學建議.

[關鍵詞] 函數;幾何;面積;模型;變式

真題呈現

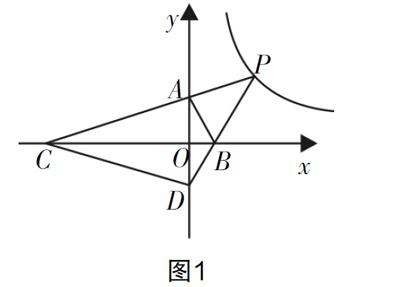
如圖1所示，在平面直角坐標系中，點A的坐標為（10，0），以OA為直徑在第一象限內作半圓，點B為半圓上的一點，連接AB并延長至點C，使得BC=AB，過點C作CD⊥x軸于點D，交線段OB于點E，已知CD=8，拋物線經過O，E，A三點，試回答下列問題.

（1）∠OBA的度數;

（2）試求拋物線的函數解析式;

（3）如果點P是拋物線上位于第一象限內的一個動點，以P，O，A，E為頂點構建四邊形POAE，記該四邊形的面積為S，則S取何值時，相應的點P有且僅有三個？

思路突破

本題目屬于二次函數綜合題，題干給出了圖像構建的過程，以及相關點坐標和線段長的條件. 其中涉及了直線、半圓和拋物線三類曲線，三小問分別求角的度數、拋物線的解析式以及研究四邊形面積，其中涉及函數和幾何等知識，需要利用坐標與方程的關系和幾何與拋物線的關系來突破. 下面對考題開展思路突破.

第一步，巧用定理，直接定角

第一問求∠OBA的度數，而點B位于以OA為直徑的半圓上，根據直徑所對圓周角定理可直接確定∠OBA=90°.

第二步，構輔助線，三點定線

第二問求經過O，E，A三點的拋物線解析式，一般將拋物線的解析式設為y=ax2+bx+c，其中含有三個參數. 從點坐標構建求解方程組角度思考，需要利用三個點的坐標，因此本題可以轉化為求O，E，A三點的坐標. 需要注意的是點O和點A分別位于x軸上，且位于對應的直線上，因此可以結合直線的解析式來求解，具體如下：

連接OC，因∠OBA=90°，則OB⊥AC，又知BC=AB，則OB為線段AC的垂直平分線，所以OA=OC=10. 分析知△OCD為直角三角形，在該三角形中OC=10，CD=8，利用勾股定理可求得OD=6，所以點C的坐標為（6，8）. 點E是直線OB和CD的交點，利用點B和點O的坐標可求得直線OB的解析式為y= x，令x=6，可得y=3，則點E的坐標為（6，3）. 所以三點的坐標分別為O（0，0），E（6，3），A（10，0），求過三點的拋物線解析式，有兩種方式，一種是將其設為通式：y=ax2+bx+c，然后將三點的坐標代入其中，可得c=0，3=36a+6b+c，0=100a+10b+c，化簡后可求得a=- ，b= ，c=0，可確定拋物線的解析式;另一種是利用拋物線與x軸交點坐標的特殊性，將其解析式設為y=ax（x-10），只需將點E的坐標代入其中即可，可求得a=- ，化簡后同樣可確定拋物線的解析式，上述兩種方法求得的拋物線的解析式均為y= - x2+ x.

第三步，模型構造，面積轉化

第三問利用圖像中的四點構建了相應的四邊形，分析面積為何值時P點有三個，因此需要對其點P的位置加以討論，并結合點P的位置來構建相應的四邊形面積模型，通過分析幾何面積來確定答案，由于四邊形的形狀不規則，可采用面積割補的方式，具體如下.

由于點P在拋物線上且位于第一象限，因此可將其坐標設為p，- p2+ p，由于圖像中點O，A，E三點的坐標固定，其中點E位于直線CD上，因此可將點P的位置分為位于CD左側和右側兩種情形來加以討論：

①當點P位于直線CD的左側時，延長OP，交CD于點Q，如圖3所示，OP的解析式為y=- p+ x，可確定點Q的坐標為6，- p+ . 對于四邊形POAE，可以視為是由△OAE和△OPE組成，而△OPE的面積可進一步拆解為S△OQE-S△PQE，所以四邊形POAE的面積可最終表示為S？荀POAE=S△OAE+S△OQE-S△PQE. 結合三角形的面積公式和關鍵點的坐標，可進一步轉化為S？荀POAE= ·OA·DE+ ·QE·Dx- ·QE·（Dx-Px）=- p2+ p+15.

②而當點P位于直線CD的右側時，延長AP交CD于點Q，如圖4所示，設AP所在直線的解析式為y=kx+b，將點P和點A的坐標代入其中，可解得AP所在直線的解析式為y=- px+ p，可確定點Q的坐標為6， . 對于四邊形POAE，同上述面積割補法，可將其面積表示為：S？荀POAE=S△OAE+S△AQE-S△PQE. 結合三角形的面積公式和關鍵點的坐標，可進一步轉化為S？荀POAE= ·OA·DE+ ·QE·DA- ·QE·（Px-Dx）=- （p-8）2+16.

當點P的位置位于CD的右側時，四邊形POAE的最大面積為16，此時點P的位置只有一個，令- p2+ p+15=16，可解得p=3± ，即在CD的左側，面積為16時點P的位置有兩個，綜合可知面積S為16時，相應的點P有三個.

解后反思

上述是初中數學常見的二次函數綜合題，其特殊之處在于將函數曲線相結合，綜合考查學生的函數與幾何知識，其中核心之問為第（2）和第（3）問，下面對其解題的關鍵點和核心方法加以探究，并對問題適度拓展變式.

1. 問題突破的關鍵步驟

上述考題的第（2）問求拋物線的解析式，需要獲得點E的坐標，而突破的關鍵一步是連接OC，確定OB為AC的垂直平分線，然后利用垂直平分線的性質定理獲得等線段長條件，這是后續求點E坐標的基礎，其突破思路也是利用幾何性質求解代數問題的典型代表. 而第（3）問屬于四邊形面積背景下的點個數問題，其突破的關鍵有兩步：一是基于點的相對位置關系對其加以分類討論，二是采用圖形割補的方法構建不規則圖形的面積模型.

2. 問題的核心突破方法

解拋物線背景下的幾何面積問題，最為有效的方法是首先利用面積割補的方式將其轉化為求解規則三角形的面積，然后利用設出坐標參數表示關鍵點和線段長，利用面積公式構建幾何面積與線段長之間關系，將幾何面積表示為關于坐標參數的函數，最后利用函數的性質來求解. 其中線段長是連接幾何面積與點坐標之間的聯系紐帶，在學習中需要強化點、線、面三者之間的關系.

3. 問題的變式拓展

第（3）問實際上是與點位置相關的幾何面積問題，對于該問還可以做出如下變式.

變式1：當以P，O，A，E為頂點構建四邊形POAE的面積為16時，求此時點P的坐標.

推薦思路 實際上該種問法與原題類似，雖未明示滿足條件的點P有三個，但充分討論后可以得出. 解析時同原問題思路，首先討論點P的位置，然后利用幾何割補的方式構建面積模型，求出所有面積為16的點坐標.

變式2：當以P，O，A，E為頂點構建四邊形POAE，試求面積最大時點P的坐標.

推薦思路 求面積最大值時點P的坐標，同樣需要對點P的位置加以討論，構建相應的面積模型. 基于考題分析，可確定點P位于CD的左側時，S=- p2+ p+15=- （p-3）2+ ，點P位于CD的右側時，S=- （p-8）2+16，由于 >16，顯然第一種情形四邊形的面積可取到最大.

教學建議

1. 注重知識關聯，綜合應用突破

上述實際上屬于函數與幾何的綜合題，在求解解析式和分析點坐標時均充分利用了相應的幾何知識，因此在教學時，除了需要引導學生掌握函數與幾何的知識定理外，還需要對兩者之間的關聯進行探究. 例如利用函數上兩點之間的點坐標可以求得線段長，分析點坐標可以確定幾何圖形的特征等. 通過對關聯知識的整合，不僅可以完善知識體系，還有利于促進解題思路的形成，這對于函數與幾何綜合題的突破是十分關鍵的.

2. 重視解后反思，形成解題策略

構建解題思路、形成方法策略是開展考題教學的意義所在，因此在教學中需要重視解后反思，引導學生挖掘問題特征，反思條件之間的關聯，貫通問題突破的思路，總結問題轉化變形的策略. 而對于一些較為典型的問題，則可以開展多解探究，從不同角度對問題加以分析，嘗試使用不同的方法解決問題. 開展多解探究不僅可以提升學生的解題能力，還可以強化學生的解題方法.

3. 深化問題變式，拓展解題思維

變式探究是中學階段十分重要的教學方式，通過變式教學可以使學生把握問題結構，認識問題本質，還可以拓展學生的視野，提升學生的解題思維. 例如上述第三問的變式探究中可以使學生認識到問題的本質是以函數為背景的幾何面積問題，因此解題時只需構建相應的面積模型，利用函數上的點坐標對其加以轉化即可. 而在教學中需要教師設置引導性問題，使學生認識到問題的核心內容，然后結合所學適度變式，增強學生的綜合能力.