基于不同參數模型的安全計算機共因失效分數計算及比較分析

高 鶯，王巨漢，張 琦，唐 濤，曹 源

(1.中國鐵道科學研究院 研究生部，北京 100081；2.中國鐵道科學研究院集團有限公司 國家鐵路智能運輸系統工程技術研究中心，北京 100081；3.北京交通大學 電子信息工程學院，北京 100044；4.中國鐵道科學研究院集團有限公司 通信信號研究所，北京 100081；5.北京交通大學 軌道交通運行控制系統國家工程研究中心，北京 100044)

列車運行控制系統作為保障鐵路運營安全的高安全苛求系統，其安全計算機在組成上多采用冗余配置。共同原因失效(Common Cause Failure, CCF)是冗余結構系統不可回避的問題，由于共同原因故障導致元器件發生關聯失效，既降低了系統的可靠性，又為系統失效(特別是系統危險側失效)埋下隱患，已成為威脅鐵路運行安全的重要因素。因此，列車運行控制系統在系統設計時，應充分考慮安全計算機共同原因失效的可能性，在系統平均危險側失效概率(PPFH)計算中也應關注共因失效分數的計算。

現有研究中計算共因失效分數的應用不少，但計算方法較統一，多使用Beta(以下簡稱“β”)參數模型，然而β參數模型對共同原因失效的原因劃分單一，不適用于高階共因失效分數計算。文獻[1]研究了外部因素導致的概率性共同原因失效及其可靠性計算，但計算內容未涉及危險側失效概率。文獻[2]對β參數模型做了改進，應用于石油工業的共因失效分數計算，但文章中沒有分析改進的模型較原模型在共因失效分數計算中有何提升。文獻[3]使用Alpha(以下簡稱“α”)參數模型計算輔助給水系統的共因失效分數，但文章沒有給出α參數模型與其他參數模型的對比。文獻[4—6]介紹了用于共因失效分數計算的多希臘字母模型，該模型實質上是現有β參數模型的細化，在高階共因失效分數計算時仍存在推廣困難。國內相關文獻[7—9]介紹了包括α參數模型在內的多種計算模型，但文獻僅限于介紹模型原理，沒有實際應用案例分析。

本文在已有文獻研究的基礎上，通過標準IEC61508中推薦的β參數模型，計算獲得計算機聯鎖系統的共因失效分數，分析該模型在計算高階共因失效分數上存在的不足；然后提出基于歷史故障數據的α參數模型的共因失效分數計算方法，并建立2種參數模型的等價關系。分別對2乘2取2冗余結構和3取2冗余結構，采用2種參數模型計算PPFH，驗證α參數模型可以獲得更加精確的共因失效分數和PPFH。

1 安全計算機PPFH計算過程

計算機聯鎖系統是列車運行控制系統的重要組成部分，圖1為該系統安全計算機的2種典型冗余結構，分別是2乘2取2結構和3取2結構。計算機聯鎖設備中驅采計算機的采集部分、聯鎖計算機的邏輯部分和驅采計算機的驅動部分共同承擔安全功能，3個子系統本身也均為冗余結構。

IEC61508-6附錄中提供了不同冗余結構的PPFH計算方法[10]。在列車運行控制系統中，冗余結構較為常見的表決組結構包括1oo2，2oo2和2oo3。3種表決組各自的PPFH計算公式為

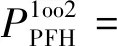
(1-β)λDUtCE+βλDU

(1)

(2)

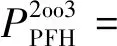
(1-β)λDUtCE+βλDU

(3)

其中，

λDU=λD(1-FDC)

λDD=λDFDC

式中：β和βD分別為無法診斷和可診斷測試識別的共因失效分數；λDU和λDD分別為未診斷和可診斷測試識別的危險側失效概率；λD單通道危險側失效概率；T1為檢驗測試時間間隔；TMTTR為平均恢復時間；FDC為診斷覆蓋率。

IEC61508中，將安全計算機劃分為輸入、邏輯計算和輸出3個子系統，安全計算機的PPFH等于各子系統PPFH之和，即

(4)

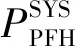
PPFH計算中，首先求得每個2oo2結構的危險側失效概率，然后以該失效概率作為1oo2或2oo3結構每個通道的危險側失效概率，計算2乘2取2結構或3取2結構的PPFH。

圖1 系統安全計算機的2種典型冗余結構框圖

由式(1)—式(3)可知，計算PPFH的公式中重要參數包括β，βD，λDU，λDD，λD，T1，TMTTR和FDC，其中共因失效分數β和βD僅能通過計算得出，其他參數可通過現場試驗數據或用戶要求獲得，因此，本文著重研究共因失效分數β和βD的計算方法以及其對PPFH計算結果影響的分析。

2 采用β參數模型計算共因失效分數

β參數模型由Fleming提出，該模型使用單一參數β定義部件由共同原因導致的失效占總失效的比例。β參數模型是當前鐵路領域計算PPFH最常用到的共因失效分數計算模型，該模型通過判斷系統是否采取防御共同原因失效的措施來確定共因失效分數。IEC61508-6附錄D中提供了防御共同原因失效的措施列表(包括分離隔離、多樣性與冗余、復雜性設計應用等8個大類[10])，并定義了每項措施的貢獻度分值X和Y。

以計算機聯鎖系統為分析對象，根據其邏輯計算和輸入/輸出3個子系統的設計要求，對照IEC61508-6中TableD.1的檢查項進行逐項打分，將分值相加得到每個子系統的X和Y值，進而根據IEC61508-6中TableD.2～3的Z值評判表確定Z值。所得的X，Y，Z值見表1。

表1 各子系統X，Y，Z值

參數S和SD的計算公式為

S=X+Y

(5)

SD=X(Z+1)+Y

(6)

將表1中的數據代入式(5)和式(6)，計算得到邏輯計算子系統的S=82，SD=139，輸入/輸出子系統的S=73，SD=118.75。

IEC61508-6中給出的S與β(SD與βD)的對應關系見表2。查表2可得：邏輯計算子系統β=1%，βD=0.5%；輸入/輸出子系統β=2%，βD=2%。

表2 β(βD)的取值

3 采用α參數模型計算共因失效分數

由上述計算過程可知，β參數模型把隨機失效單純分為2類，即獨立失效(有且只有1個通道發生失效)，共同原因失效(所有通道失效，且失效原因相同)。對于3階冗余結構的系統(如3取2結構)，β參數模型認為2通道失效的概率為零，系統只存在單通道失效以及3通道同時失效2種情況。因此在計算3重及3重冗余以上的共因失效分數時，β參數模型的計算結果存在偏差。同時，該模型采用查表分析法，計算結果對應取值的區間大且分類簡單(詳見表2)，也不利于獲得精確的共因失效分數。

列車運行控制系統的冗余結構通常為2通道和3通道，為了計算更加精確的PPFH，本文引入在核電領域使用的α參數模型。首先通過模型的構建原理證明其更適合于3階及以上冗余結構的共因失效分數計算，進而針對鐵路領域安全計算機缺乏共同原因失效歷史統計數據的問題，結合美國核管理委員會(United States Nuclear Regulatory Commission, U.S.NRC)的先驗參數，獲得列車運行控制系統安全計算機不同冗余結構下的共因失效分數。

(7)

其中，

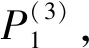
P(A)=P(CA)+P(CAB)+P(CAC)+P(CABC)

(8)

其中，

對于3取2結構的安全計算機，如果系統中2個或2個以上通道失效時系統不再安全，那么，在計算該系統由共因失效導致的危險側失效概率時，PPFH應包含2通道共同原因失效和3通道共同原因失效2類，即

(9)

(10)

同理，可得2乘2取2結構的俺全計算機，式(1)中β與α因子的關系為

β=α2

(11)

在應用α參數模型計算PPFH時，需確定變量αk，k=1,2,…,m。由于目前我國列車運行控制系統缺少針對安全計算機中共同原因失效數據的統計，在確定α參數模型的變量αk時，本文參考了美國核管理委員會在核能發電領域發布的年度共同原因失效統計結果，并將其作為變量αk計算的先驗數據進行修正[12-13]。

首先αk的先驗數據服從β分布，即

(12)

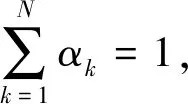
(13)

式中：ak指系統發生k個通道共同原因失效的次數；bk指除了發生k個通道共同原因失效外，其他類型失效發生的次數。

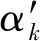
(k=1,2,…,m)

(14)

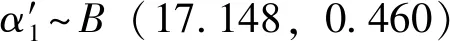
將表3、表4中αk值分別代入式(10)、式(11)，計算得到3取2結構和2乘2取2結構安全計算機的共因失效分數β，結合IEC61508-6中定義的β=2βD，進而通過式(1)—式(3)計算獲得采用α參數模型的PPFH。

表3 2乘2取2冗余結構αk值

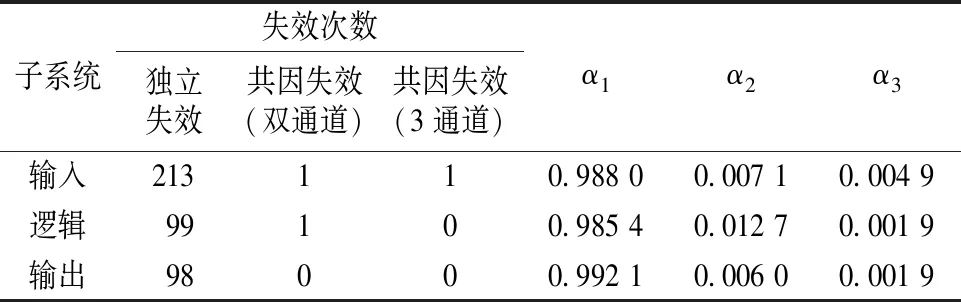
表4 3取2冗余結構αk值

4 計算結果及對比分析

根據既有計算機聯鎖系統的可靠性數據，取輸入子系統的λD=1.00×10-7次·h-1，FDC=90%；邏輯計算子系統的λD=3.80×10-7次·h-1，FDC=99%；輸出子系統的λD=5.00×10-7次·h-1，FDC=90%；3個子系統的T1=8 760 h；TMTTR=1 h。

4.1 2乘2取2結構安全計算機的危險側失效概率計算

針對2乘2取2結構，分別采用β參數模型和α參數模型，計算得到共因失效分數β和βD，然后代入式(1)和式(4)，可分別計算得到由獨立失效(獨立故障原因)或由共因失效(共因故障原因)導致的危險側失效概率，計算結果見表5和表6。

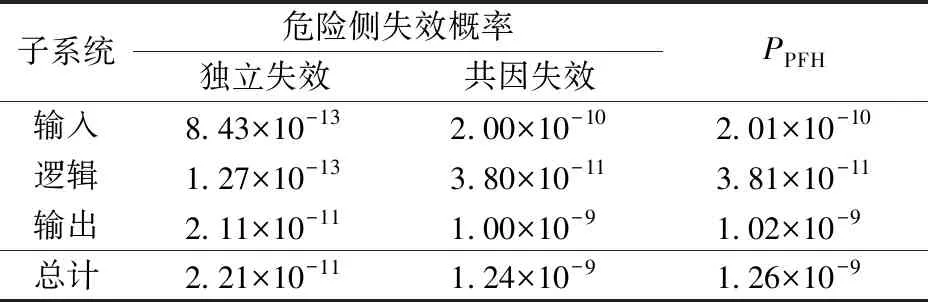
表5 使用β參數模型的計算結果(2乘2取2結構)

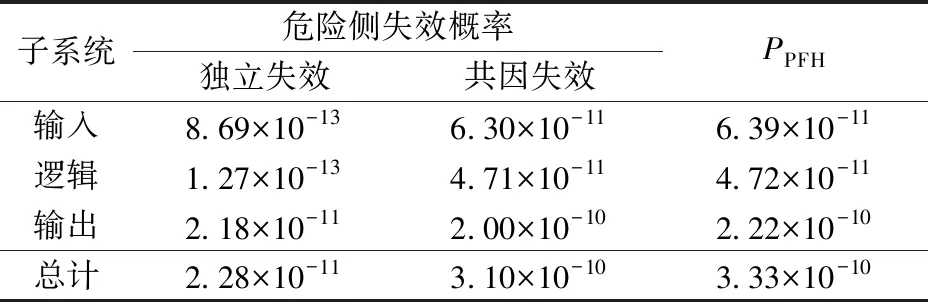
表6 使用α參數模型的計算結果(2乘2取2結構)

圖2顯示了2乘2取2結構下，分別采用β參數模型和α參數模型時3個子系統的PPFH計算結果，可以明顯看出，兩者差別較大。圖3顯示了2種參數模型下共因失效導致的危險側失效概率。將圖3與圖2對比可知：共因失效導致的危險側失效概率約等于PPFH的計算結果，說明共因失效分數是決定PPFH計算結果的重要參數。

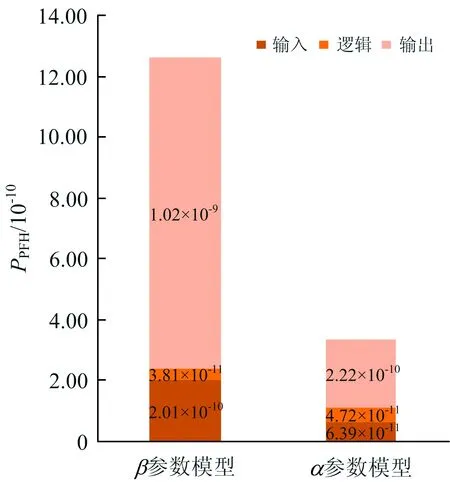
圖2 2種參數模型計算PPFH對比

圖3 共因故障導致的危險側失效概率對比

4.2 3取2結構安全計算機的危險側失效概率計算

針對3取2結構，分別采用β參數模型和α參數模型，計算得到共因失效分數β和βD，然后代入式(3)和式(4)，可分別計算得到由獨立失效(獨立故障原因)或由共因失效(共因故障原因)導致的危險側失效概率，計算結果見表7和表8。

由表5—表8可知：基于當前歷史數據的α參數模型較β參數模型得到的PPFH更小，其原因在于當前用于計算共因失效分數的故障數據有限，當隨著設備或相似設備的共同原因失效數據累積，對應的αk被不斷修正，該模型計算的PPFH與實際情況較接近。

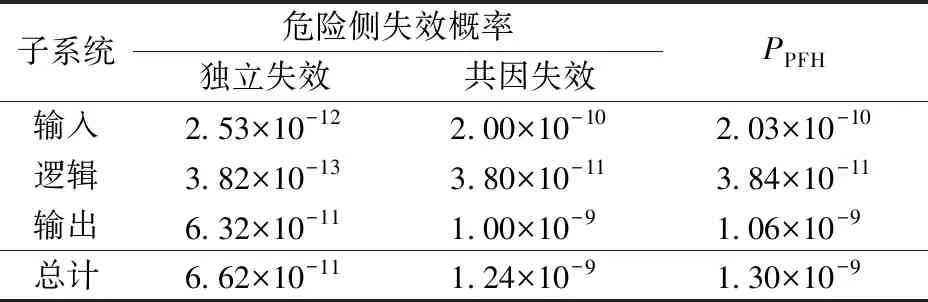
表7 使用β參數模型的計算結果(3取2結構)

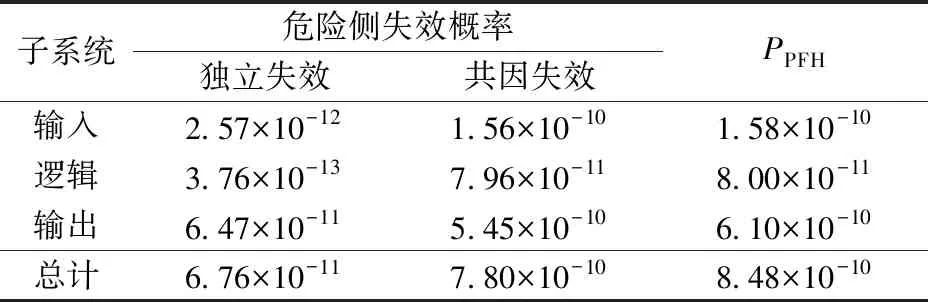
表8 使用α參數模型的計算結果(3取2結構)

4.3 采用2種參數模型時2種冗余結構危險側失效概率的對比

結合4.1節和4.2節的計算結果，針對不同冗余結構，采用2種參數模型分別計算由獨立失效(獨立故障原因)或由共因失效(共因故障原因)導致的危險側失效概率，如圖4和圖5所示。

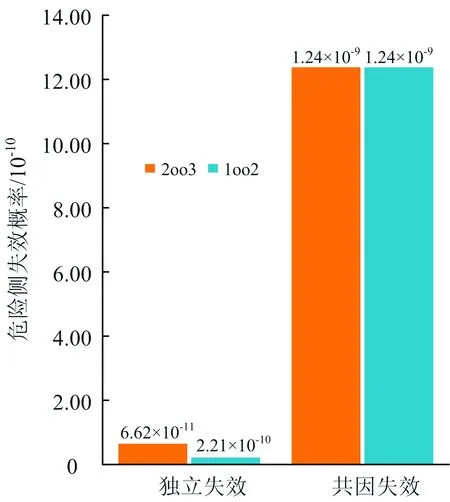
圖4 采用β參數模型時不同冗余結構PPFH組成

對比圖4和圖5可知：基于2乘2取2結構和3取2結構計算得到的PPFH中，共同原因失效對其貢獻度大于獨立失效，且α參數模型計算得3取2結構的共同原因危險側失效概率高于2乘2取2結構，與實際情況相符；α參數模型能夠區分不同冗余結構下獨立失效和共同原因失效導致的危險側失效概率，但β參數模型中無法區分共同原因失效導致的危險側失效概率，這也是該模型不適用于高階共因失效分數計算的原因之一。

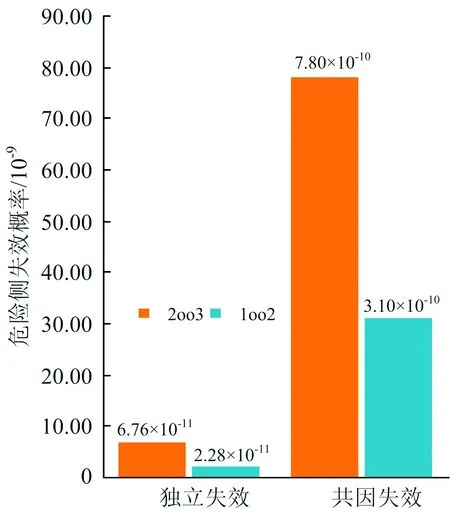
圖5 采用α參數模型時不同冗余結構PPFH組成

5 結 語

以計算機聯鎖設備為安全計算機研究對象，分析了經典β參數模型計算共因失效分數的不足，提出引用核能領域的α參數模型計算共因失效分數，同時采用先驗分布解決了列控系統安全計算機缺乏共同原因失效統計數據的問題。對計算機聯鎖系統安全計算機的2種常見冗余結構，分別采用這2種參數模型計算其共因失效分數，從而計算PPFH和共同原因失效導致的危險側失效概率。結果表明：共因失效導致的危險側失效概率是PPFH的主要組成部分，α參數模型能夠量化計算3重及以上冗余結構的共因失效分數，并獲得更符合實際輸出的PPFH計算結果。同時，當共因失效數據不斷完善時，α參數模型可以通過修正后驗參數獲得更準確的共因失效分數，為驗證安全計算機安全完整性等級提供有利幫助。