零售商公平關切與創新投入的混合渠道供應鏈均衡策略
(廣西財經學院 工商管理學院,廣西 南寧 530003)
1 引言
近年來供應商普遍建立網絡直銷渠道,與此同時由于顧客零售商忠誠、購買習慣和體驗、服務支持等原因,混合多渠道模式被眾多供應商采用,并引發與傳統渠道的渠道沖突。為緩解渠道沖突與提高供應鏈協作,一些學者圍繞傳統零售商,從促銷努力、廣告、定價等方面進行了深入研究,如Tsay和Agrawal[1]研究了需求受促銷影響下網絡直銷、傳統零售和混合渠道三種不同渠道方式對各方的影響與策略。Dumrongsiri等[2]分析了兩個渠道服務與分銷成本差異對混合渠道供應鏈的影響。Xie等[3]研究了合作廣告影響需求情況下混合渠道供應鏈決策問題。
以上文獻均假設供應鏈成員理性決策。近年來大量行為實驗表明,人們做決策時常因非理性導致決策的偏差,并發現不少決策者關注是否得到公平待遇,由此影響他們的決策和供應鏈收益[4~6]。Cui等[4]最早地將公平關切引入到供應鏈研究,發現若供應鏈成員關注渠道公平,在線性需求下設置適當的批發價契約就可以實現供應鏈協調。此后一些學者又進一步考慮混合渠道供應鏈,如邢偉等[7]發現在零售商公平關切時,零售商市場份額對混合渠道供應鏈雙方均衡和利潤造成影響。Liu等[8]研究了下游零售商公平關切并存在顧客搭便車情況對混合渠道供應鏈成員的影響。Li等[9]分析了傳統零售商公平關切且提高單位產品服務水平情況下的供應鏈成員定價與服務博弈,曲優等[10]則考慮了公平關切與損失規避情況下的混合渠道訂貨問題。
盡管上述文獻從傳統零售商出發,多個角度研究了混合渠道供應鏈的沖突與協調,但在模型構建上都沒有考慮混合渠道存在性對供應鏈成員定價的限制和決策的影響,對零售商的創新投入也研究得較少。事實上現有對供應鏈創新協作的研究,仍主要局限在非電子商務環境的傳統供應鏈,如Gilbert和Cvsa[11]研究發現創新投入的溢出效應以及上游機會主義行為,導致分銷商降低運作成本的創新投入下降。Wang和Shin[12]比較了三種不同契約對供應商創新決策,及供應鏈成員收益的影響。Jose等[13]則通過實證研究了企業不同產品特性、能力、創新內容等差異對創新的影響。Kim和Netessine[14]比較了供應商和制造商承諾及委托代理下的菜單選擇兩種情況下的創新努力和成員間收益。徐偉等[15]分析了制造商創新投入與成員成本分擔下供應鏈整體最優決策及利潤。少數涉及混合渠道供應鏈創新投入研究的文獻,如文獻[16,17],也都沒有考慮供應鏈成員公平關切。對傳統零售商來說,在混合渠道環境下如何不斷創新投入,提高運營效率和競爭力對其自身具有重要意義,同時也對供應鏈績效產生影響;另外考慮其在供應鏈中處于相對不利位置,考慮公平關切因素更具有現實意義[9]。
鑒于此,本文基于混合渠道供應鏈存在性的約束條件,在考慮零售商公平關切因素情況下,對混合渠道供應鏈中零售商創新投入時的供應鏈成員的博弈和策略進行了研究,得到了零售商創新投入力度、各方定價的最優決策與利潤,并分析了網絡渠道潛在需求份額和零售商公平關切程度對供應鏈成員的影響,提出了供應鏈協調契約。
2 問題描述與模型假設
考慮由一個供應商和一個零售商組成的混合渠道供應鏈生產并銷售某產品。供應商開設網絡直銷渠道,以價格p1將產品直接銷售給顧客,同時以批發價w將產品批發給零售商;零售商在發生邊際分銷成本cr后,在傳統渠道以零售價p2將產品銷售給顧客。另外基于網絡渠道分銷成本優勢,為簡化分析且不影響主要結論,假設供應商網絡直銷渠道分銷該產品的邊際成本為0[7,18]。
(1) 兩個渠道的市場需求函數分別為[19]
(1)
其中下標1, 2分別代表網絡和傳統渠道;a為該產品總潛在需求量,s和1-s分別為網絡與傳統渠道所占份額,反映了顧客渠道消費偏好,0
(2) 與網絡渠道相比,現實中傳統渠道銷售費用往往較高,因此其產品售價也較高。為提高競爭力,零售商通過創新投入在物流、庫存等運作成本上挖掘潛力,可降低邊際分銷成本。同文獻[11,14],假設零售商投資c(θ)可將自己的邊際分銷成本cr降低θr(r為邊際成本最大可減少量,反映其創新潛力,0≤θ<1,r
(3) 零售商具有較強的公平關切,當感覺不公平時可能直接影響他加入供應鏈及進行創新投入的意愿。本文分零售商公平中性和公平關切兩種情況,分析公平關切因素對供應鏈成員決策的影響。
3 模型分析
供應商和零售商的利潤πS,πR分別為
πS=p1d1+wd2
(2)
πR=(p2-w-cr+rθ)d2-ηθ2
(3)
其中πS包括從網絡直銷渠道的銷售收益和傳統渠道的批發收益,πR則包括傳統渠道的銷售收益與創新投入成本。
要使2個渠道都存在,相關參數需要滿足以下條件:(1)p1≥w+cr-rθ,否則零售商直接從網絡渠道采購的成本將低于自己渠道的運營成本,引發零售商不滿,并放棄從傳統渠道進貨和進行創新投入;(2)p2≥w+cr-rθ,否則零售商無法贏利而不會經營傳統渠道;(3)d1≥0,d2≥0。由此可得到約束
(4)
由于創新投入通常要先期進行,并可能由于其沉沒成本與轉換成本,產生“套牢”問題[11]。考慮如下三階段Stackelberg動態博弈:首先零售商在預期供應商反應的情況下確定創新投入力度θ,隨后供應商確定w和p1,最后零售商決定p2。
為進行對比,以下首先分析當零售商公平中性時的情況,并將其與集中決策模式對比,接著討論零售商公平關切下創新投入的雙方均衡策略。
3.1 零售商公平中性時創新投入
在該情形下不考慮零售商公平關切,假設雙方都是公平中性的,以最大化各自的利潤為目標分別決策。下面采用逆序方法分析,在第三階段零售商的優化問題是
maxπR(p2|θ,p1,w)=(p2-w-cr+rθ)d2-ηθ2
(5)
由一階條件易知
p2(θ,p1,w)=[(1-s)a+cr+w-rθ+p1λ]/2
(6)
(6)式表明,p2隨該渠道市場潛在需求量(1-s)a、cr以及p1和w的增大而增大,隨創新投入降低的邊際分銷成本rθ的增大而減小。后者說明創新投入提高了傳統渠道零售商的市場競爭力。
將(6)式和(1)式代入(2)式,得到供應商第2階段的優化問題為
maxπS(p1,w|θ)=p1d1(p1)+wd2(p1)
s.t.p1≥w+cr-rθ
(7)

情況1當拉格朗日乘子μ=0時,得到
(8)
而p1-w-cr+rθ≥0,即需s≥s*=(cr-rθ)(1+λ)/(2a)+1/2。
依次將(8)、(6)式代入(3)式,由?2πR(θ)/?θ2=-(16η-r2)/8<0,故πR(θ)是關于θ的凹函數,由一階條件得零售商的最優創新投入力度為
θN*=r[(1-s)a-cr]/(16η-r2)
(9)
將(9)式依次回代上面各式,得到命題1。
命題1當1>s≥s*時,在公平中性的零售商進行創新投入情形下,供應鏈博弈的均衡結果有以下結論:

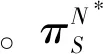
情況2當μ>0時,此時p1-w-cr+rθ=0。得到

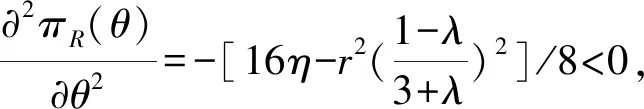
(10)
顯然,?θN**/?r>0,?θN**/?η<0。
以上說明,當0 類似情況1的推導,依次將(10)式回代p1(θ)和w(θ)及(6)式、(3)式,可得各方最優決策和零售商利潤為 為表達簡潔,這里記A=4η(3+λ),B=2sa+cr(1-λ)。 這里由上面分析,給出命題2。 為比較分散決策與零售商公平關切對供應鏈整體的影響,本節以供應商和零售商縱向整合的集中決策模式為參照。此時不存在公平關切對供應鏈的影響,并且w作為兩者間的利潤分配手段不再存在,供應鏈只須確定p1,p2,θ,以使整體利潤πSC最大,其優化問題是maxπSC(p1,p2,θ)=p1d1+(p2-cr+rθ)d2-ηθ2。 公平關切(不公平厭惡)是一種社會偏好行為,指人在關注自身利益的同時,還會關注他人的利益,并進行公平比較。Fehr和Schmidt[5]基于結果公平建立了線性的公平關切FS模型。借鑒該模型,本文主要考慮零售商劣勢不公平厭惡(嫉妒偏好)情形,采用如下效用函數表示公平關切下的零售商效用[10]:UR=πR-δ(πS-πR)。其中參數δ為零售商的劣勢不公平厭惡系數,假設δ>0,為雙方的共同知識;顯然當δ=0時,零售商即為3.1節的公平中性情況。由于零售商渠道的局限性,假設零售商公平關切于供應商傳統渠道的收益wd2與自身收益和創新投入的比較,故可以將零售商效用修正為 UR=πR-δ(wd2-πR) (11) 依然采用逆序分析。在博弈的第三階段零售商確定自己銷售價p2時面臨的優化問題是maxUR(p2|θ,p1,w)=πR-δ[wd2-(p2-w-cr+rθ)d2+ηθ2]。 由一階條件得到零售商效用的最大值點 (12) 比較(12)式、(6)式可以發現,與公平中性情況相比,第3階段零售商在公平關切下其零售價提高了,多了一個與w相關的增加項,當w和δ越大,該增加項越大。 基于零售商的反應,將(12)式代入(2)式,得到供應商第2階段的優化問題是 maxπS(p1,w|θ)=p1d1(p1)+wd2(p1) s.t.p1≥w+cr-rθ (13) 情況1當拉格朗日乘子μ=0時,得到 (14) (15) 這里記C=(1-s)a-cr+rθ,D=(1+δ)(1+2δ),E=sa+(cr-rθ)λ。 將(14)式、(15)式代入(13)式的約束條件,知此時須 Fsa-G(1-s)a≥H(cr-rθ) (16) 記常數F=(1+δ)(4-4λ+8δ-6δλ),G=(1+δ)[4-4λ+4δ-(7-λ)δλ],H=4(1+δ)·(1+3δ)(1-λ2)-δλ(1+δ-λ) 。 將(12)式、(14)式及(15)式依次代入(11)式,顯然?2UR(θ)/?θ2<0,由一階條件得到零售商最優創新投入力度 (17) 依次將(17)式代入(15)式、(14)式、(12)式及(2)式、(3)式,可得各方最優決策和利潤。 情況2當拉格朗日乘子μ>0時,類似3.1節,此時(13)式的約束條件是緊的,得到對應的博弈最優策略為 記I=1+δ,J=(1-λ)2-δ(1-λ)(1+5λ)-δ2[2+λ(1-4λ)]。 同情況1,依次回代可得各方最優決策和利潤。易驗證當δ=0時,本節結果即轉化為零售商公平中性情況的3.1節。盡管由前面分析得到了本文相關決策的最優解析解,但由于其過于復雜,故借助數值算例分析,來驗證本文相關結論及得到一些新的管理學意義[10,18]。 首先設定基本參數如下:a=400,λ=0.3,η=200,r=4,cr=8。 取零售商劣勢不公平厭惡系數δ=0.5。經計算發現:s分界點s*和s**分別是0.51和0.41,公平關切使s分界點變小;由(4)式約束條件得到s的可行區間為(0, 0.72),即當s超過0.72時混合渠道不存在。另外由θN*-θF*=0.02s+0.0073>0,θN**-θF**=0.28-0.41s>0,表明公平關切使得零售商的創新投入力度減小。關于s對供應鏈成員的影響,如圖1~圖3所示。 由圖1發現,與零售商公平中性相比,當零售商公平關切時,供應商的網絡零售價p1和傳統渠道批發價w降低,零售商零售價p2提高。另外無論零售商公平態度如何,p1都隨s的增大而增大,p2都隨s的增大而減小,但w為先增后減,其分界點分別為s*和s**,且過了分界點后價格隨s變化的速度更快。 由圖2,公平關切使得網絡渠道市場需求d1提高,傳統渠道市場需求d2降低。而由圖3發現:由于零售商創新投入的“套牢”效應及渠道競爭,使其在分界點s*和s**左邊的情況2下利潤曲線較平滑,市場需求份額增加對利潤改善并不顯著。另外,與零售商公平中性相比,零售商公平關切提高了自身利潤,使供應商利潤降低,這是由于零售商公平關切特性使他在合作中提高了博弈能力,因此提高了利潤,但也使雙方的決策更加扭曲,整個供應鏈收益降低。最后隨著s的增加,零售商公平關切對各方利潤及供應鏈整體利潤的影響變小,分散決策與集中決策下供應鏈整體利潤差距也減小。 注:曲線1、3、5分別是公平中性下的p1、p2、w,曲線2、4、6分別是公平關切下的p1、p2、w。 圖1s對供應鏈成員定價的影響 注:曲線1、3分別是公平中性下的d1、d2,曲線2、4分別是公平關切下的d1、d2。 圖2s對供應鏈成員需求量的影響 取s=0.6,由于s>0.51,此時零售商公平關切屬于3.3節的情況1。由圖4,傳統渠道零售價高于網絡零售價,并且隨著δ的增大,供應商批發價和網絡零售價逐漸降低,而傳統渠道的零售價將會提高。而由圖5發現,零售商公平關切程度將影響其創新投入的積極性,θ隨著δ的增加而減小。為使雙方通過緊密合作得到更大收益,提出如下契約協調供應鏈。 證明考慮(11)式及3.2節中maxπSC(p1,p2,θ)表達式,不難發現在該契約下零售商決策的θ將與3.2節供應鏈集中決策下一致,另外通過調整f的范圍可使得雙方都得到Pareto改善,即得證。 結合圖3、圖5發現,該契約使得供應商通過適當讓利,激勵零售商提高了創新投入力度,使供應鏈整體協調,雙方達到雙贏。并且由圖3的分析,顧客傳統渠道潛在需求份額越高(s較小)時,該契約效果將越顯著。 圖5 δ對零售商創新投入力度θ的影響 近年來,隨著網絡零售的快速增長,傳統零售商面臨渠道沖突、經營成本高、客戶流失等嚴峻挑戰。本文基于混合渠道需求的相互影響和存在條件,對公平關切對零售商創新投入的影響及供應鏈成員的博弈和策略進行了研究:(1)分析發現在創新投入發生“套牢”效應的情況下,供應商將基于渠道潛在需求份額、渠道需求轉移系數、零售商的創新投入和公平關切等情況,采用兩個不同策略。(2)得到了雙方的決策和收益,發現都無法達到供應鏈整體最優。(3)公平關切降低了零售商創新投入力度,提高了自身利潤,但整個供應鏈利潤降低。(4)證明價格協作加收益分享的混合契約使雙方緊密合作,供應鏈整體達到最優,該契約在傳統渠道需求份額越高時效果越顯著。本文研究對管理的啟示是:在當前激烈的混合渠道競爭中,傳統零售商公平關切和渠道努力將分別對供應鏈整體帶來不利和有利的影響,針對其要求采取相對的價格協調策略將提高供應鏈績效。另外本文對供應鏈成員借助不同渠道優勢展開合作,建立關系緊密的OAO(online and offline)供應鏈具有啟示意義。 本文主要考慮了混合渠道供應鏈中傳統零售商公平關注且進行創新投入,未來研究可以拓展考慮混合渠道供應鏈多成員創新、公平關切信息不對稱等情況對供應鏈的影響及協作策略。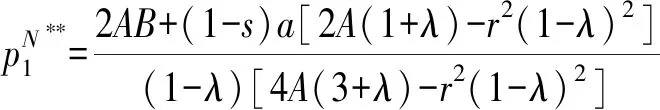
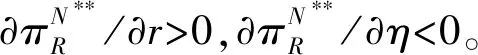



3.2 混合渠道供應鏈集中決策模式

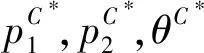

3.3 零售商公平關切下創新投入

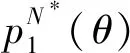




4 算例分析
4.1 網絡渠道潛在需求份額s對供應鏈成員的影響


4.2 零售商公平關切程度δ對供應鏈成員的影響


5 結論與啟示

