基于LME/BME的珠江三角洲PM2.5星地融合技術研究

周 爽,王春林,孫 睿,湯 靜,黃 俊,沈子琦

?

基于LME/BME的珠江三角洲PM2.5星地融合技術研究

周 爽1,2,王春林2,3*,孫 睿1,湯 靜3,黃 俊3,沈子琦3

(1.北京師范大學地理科學學部,遙感科學國家重點實驗室,北京 100875；2.中國氣象局廣州熱帶海洋氣象研究所,廣東 廣州 510640；3.廣州市氣候與農業氣象中心,廣東 廣州 511430)

收集并處理了遙感反演的氣溶膠光學厚度(AOD)、歸一化植被指數(NDVI)和氣象數據,采用貝葉斯最大熵(BME)結合線性混合模型(LME)估算了2015年10月~2016年3月珠江三角洲地區近地表旬平均PM2.5質量濃度.結果表明,LME+BME 模型的預測精度比LME 模型有較大提升,LME+BME模型的交叉驗證結果2為0.751,RMSE為6.886μg/m3,MAE為4.52μg/m3,而LME模型的交叉驗證結果2為0.703, RMSE為7.546μg/m3, MAE為4.927μg/m3.空間分布看,PM2.5高濃度地區主要集中在廣州、佛山、東莞等地區,低濃度地區主要集中在肇慶、惠州、江門的南部等地區;時間變化看,PM2.5污染比較嚴重的時間為2015年10月中旬、2015年11月下旬以及2016年3月下旬,而2015年10月上旬、2015年12月上旬和2016年1月下旬污染則相對較低.

PM2.5；MODIS AOD；線性混合模型；貝葉斯最大熵；珠江三角洲

珠江三角洲是我國經濟發展和城市化水平較高區域,也是大氣PM2.5污染嚴重、霾頻發的區域[1-2].如何獲得空間連續、質量可靠的地表PM2.5分布對于環境氣象預報、空氣污染減排決策、流行病學中PM2.5人口暴露及健康影響評估等意義重大[3-4].

已有研究表明,衛星遙感的方法可以有效彌補地面監測站監測空間范圍較小的不足,而遙感估算PM2.5是基于衛星遙感反演產品-氣溶膠光學厚度(AOD)展開的.早期的研究利用AOD反演近地面PM2.5多基于簡單線性回歸模型[5-6],近年來有學者利用多種更為復雜的方法描述二者之間的關系,如土地利用回歸模型[7-9]、地理加權回歸模型[10-12]、基于遙感瞬時估算的半經驗-物理方法[13-16],這些模型的局限在于沒有考慮PM2.5-AOD關系隨時間變化的差異性.Lee等[17]首次提出了一種包含固定效應和隨機效應的混合效應的線性混合模型(LME)來反映AOD和PM2.5濃度的日差異性關系,該模型在美國東北部PM2.5濃度反演和實測值的相關性高達0.92.將此模型運用到美國其他地區,也得到了很好的驗證[18-19].我國已有學者將LME運用到京津冀[20-21]、長江三角洲[22]、珠江三角洲[20]等地區的PM2.5濃度估算研究當中,都取得了比較好的效果.

本文通過引入貝葉斯最大熵(BME)以提升模型模擬精度,現代時空地統計學BME 作為一種時空數據分析方法,其優勢在于能綜合利用不同來源的不確定性數據,顯著提高未采樣點的估計精度.近年來,BME統計方法被逐漸用于地面實測數據與遙感數據的融合,Yu等[23]將LUR模型中結合BME,對臺北地區PM2.5分布制圖, 使得平均誤差從2.78μg/m3降低至2.15μg/m3.此外在美國PM2.5時空特性研究[24]中發現,對LUR輔助變量加入遙感數據并引入BME后, RMSE由15.91μg/m3降低至4.63μg/m3.另有學者將LME結合BME,對中國沿海部分省市進行PM2.5估算[25],結果表明LME+BME方法與僅使用LME模型的結果相比R2有所提升且誤差有所下降.

本文以珠江三角洲為研究區域,結合高分辨率AOD數據、氣象數據以及美國國家環境預報中心(NCEP)再分析資料,基于LME及BME模擬地表逐旬PM2.5濃度分布,為珠江三角洲地區的PM2.5污染監測預報、治理決策及健康影響評估等提供核心數據支撐.

1 研究數據與方法

1.1 研究區域與數據

1.1.1 研究區域與PM2.5實測數據 珠江三角洲包括廣州、深圳、佛山、東莞、惠州、中山、珠海、江門、肇慶,共有56個空氣質量國控站點(圖1).本研究采用2015年10月~2016年3月逐日PM2.5,經過質量控制后合成各站點旬平均PM2.5.

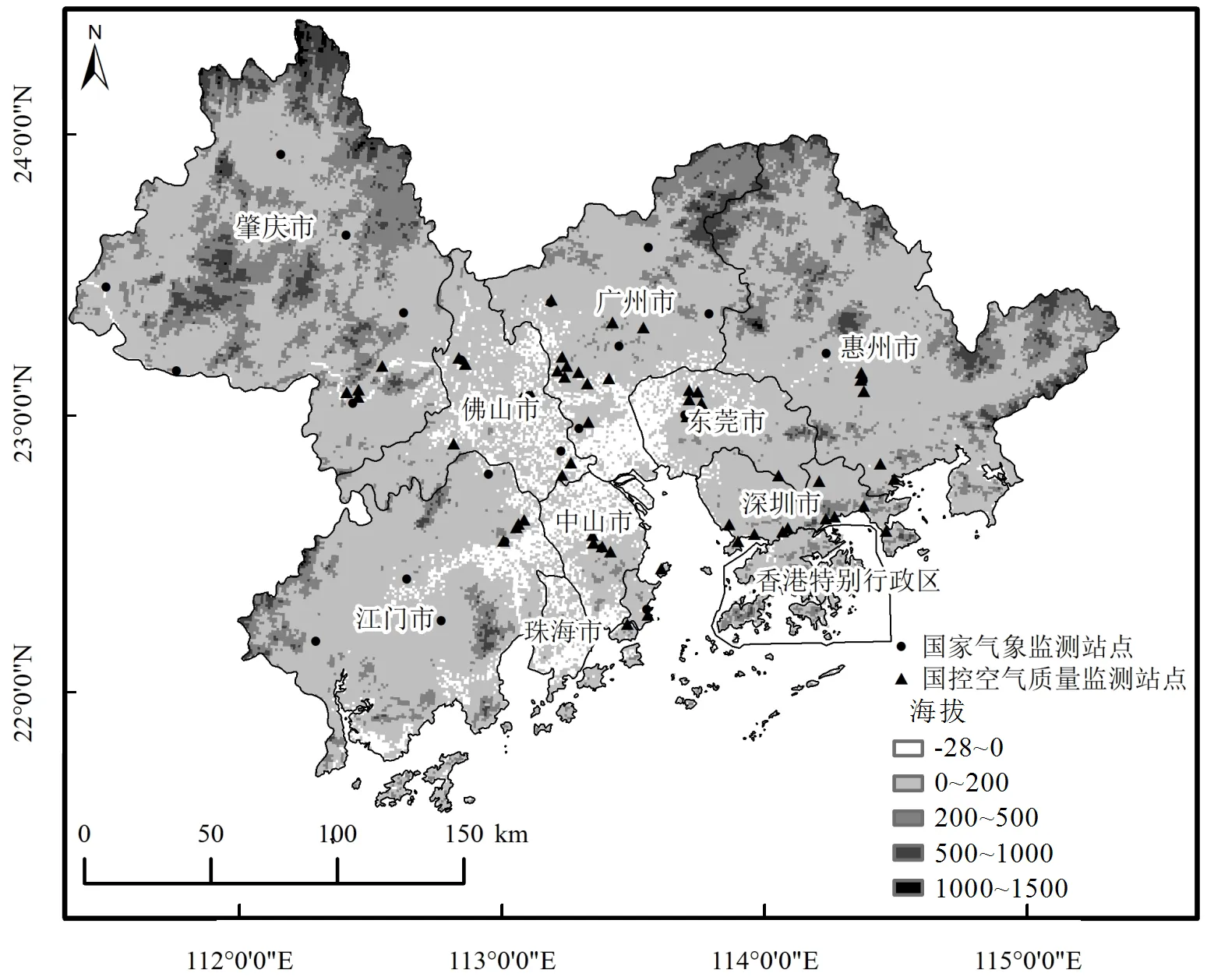
圖1 珠江三角洲地面PM2.5 及氣象國控監測站

1.1.2 氣象數據 地面氣象數據包括珠江三角洲29個國家氣象站點2015年10月~2016年3月逐日能見度()(將其轉換為消光系數=3.912/)、相對濕度(RH)、風速(WS)數據,經過質量控制后合成旬平均數據,利用克里金插值算法形成1km×1km網格數據.

邊界層高度(PBLH)采用NCEP GDAS/FNL再分析數據,水平分辨率為0.25°×0.25°,時間分辨率為6h(UTC 00/06/12/18),將一天中4個時段合成為日平均PBLH, 再將10d的PBLH合成為旬平均PBLH,利用克里金插值算法形成1km×1km網格數據.

1.1.3 遙感數據 本文所用遙感數據有MODIS AOD產品以及歸一化植被指數(NDVI) 數據,均下載自NASA的LAADS網站(http://ladsweb. nascom.nasa.gov/).AOD數據采用2015年10月~ 2016年3月MODIS 3km AOD產品,空間分辨率為3km,時間分辨率為2次/d.采用10:30過境的Terra MODIS AOD和13:30過境的Aqua MODIS AOD合成逐日AOD,將10d的AOD合成為旬平均AOD,利用克里金插值方法形成1km×1km網格數據; NDVI 采用MODIS NDVI 16d合成產品,空間分辨率為500m,重采樣形成1km×1km網格數據. 2015年10月~2016年3月逐旬NDVI按照時間臨近原則選取.

1.2 研究方法

本文以旬平均 PM2.5、AOD 及相關氣象資料為基礎,采用貝葉斯最大熵(BME)結合線性混合模型(LME)構建珠江三角洲1km×1km 分辨率逐旬PM2.5數據集,并對估算結果進行驗證評估.

1.2.1 線性混合回歸模型(LME) 本文利用AOD及氣象因子構建了包含固定效應和隨機效應的LME模型,固定效應部分包括固定截距及AOD等6個自變量的固定斜率,隨機效應部分為AOD隨旬變化的隨機斜率.固定效應影響總體均值,隨機效應與抽樣過程有關,對數據的協方差結構有貢獻.

LME模型公式為:

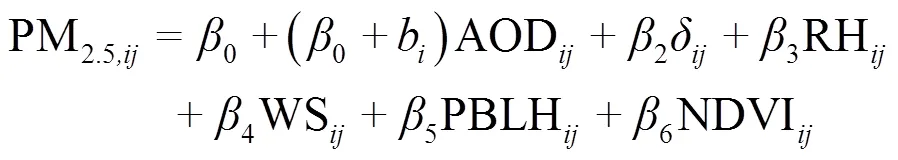
式中:下標、分別表示旬和站點序號,PM2.5為地面實測PM2.5濃度,μg/m3,AOD為氣溶膠光學厚度,為地表消光系數,km-1;RH為相對濕度,%;WS為地面10m平均風速,m/s;PBLH為邊界層高度,km;NDVI為歸一化植被指數;0為固定截距,1~6為各自變量的固定斜率;b為AOD隨旬變化的隨機斜率.

1.2.2 貝葉斯最大熵(BME) 貝葉斯最大熵(BME)是由George Christakos在1990年提出的一種基于認知學的時空數據分析方法[26],其最大的優勢在于能夠綜合利用各種來源不同的不確定性數據,顯著地提高未采樣點的估計精度[27].本文BME方法基于Seks-gui時空分析軟件包,一般知識為地面實測PM2.5濃度的時空平穩趨勢和協方差函數,特定知識包括硬數據和軟數據兩部分,硬數據為地面實測PM2.5濃度,軟數據為以LME模擬值為均值,以RMSE為區間構建的均勻分布,輸入BME得到融合軟、硬數據的PM2.5格點數據.

BME估計可由式(2)獲得:

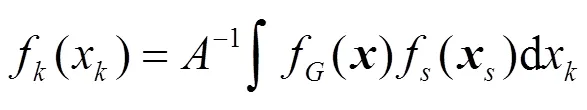
式中:G()是由一般知識獲得的關于的先驗概率密度函數,f(x)是軟數據的概率密度函數,f(x)是在估計點k的后驗概率密度函數,是歸一化常數.

根據后驗概率密度函數,可以式(3)計算得到估計點處的估計均值.

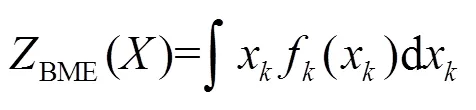
2.3 模型驗證

本文采用十折交叉驗證的方法來驗證和比較LME和LME+BME的模型精度,并基于可決系數(2)、平均絕對誤差(MAE)和均方根誤差(RMSE)來評估兩種模型的預測精度.

2 結果分析

2.1 PM2.5與AOD、氣象數據相關分析

本文在進行數據匹配及預處理后,對2015年10月~2016年3月實測旬平均PM2.5濃度的變化進行了箱形圖分析(圖2),可以看出,研究期間旬平均PM2.5的變化呈現出一定的周期性波動,并且站點離差在不同旬也有所不同,其中2015年10月中旬PM2.5濃度最高,且站點之間離差也最大(超過40μg/m3).

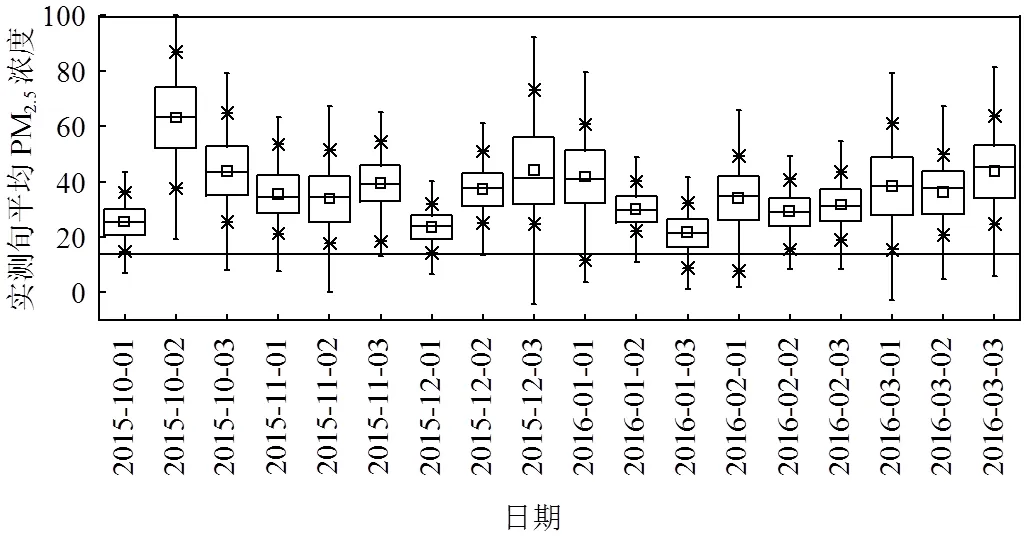
圖2 2015年10月~2016年3月實測PM2.5旬平均值

PM2.5與AOD、、RH、WS、PBLH、NDVI等6個自變量點聚圖相關分析如圖3,可以看出,逐旬平均AOD、與PM2.5呈顯著正相關關系,說明地表PM2.5濃度對地表消光乃至整個大氣柱的消光AOD密切相關;WS、PBLH與PM2.5呈現顯著負相關關系,表明地表風速越大、邊界層越高通風量越大,越有利于污染物擴散而不容易積聚; RH與PM2.5呈負相關關系,可能與RH、PM2.5季節變化反相位特征有關,一般珠江三角洲干季(10~3月)相對濕度較低但PM2.5濃度較高;NDVI與PM2.5呈負相關關系,表明地表植被較好的區域(郊區)、季節(夏季)對應較低的PM2.5濃度,與郊區氣溶膠污染源排放較少及植被對氣溶膠顆粒物具有吸附清除作用有關.

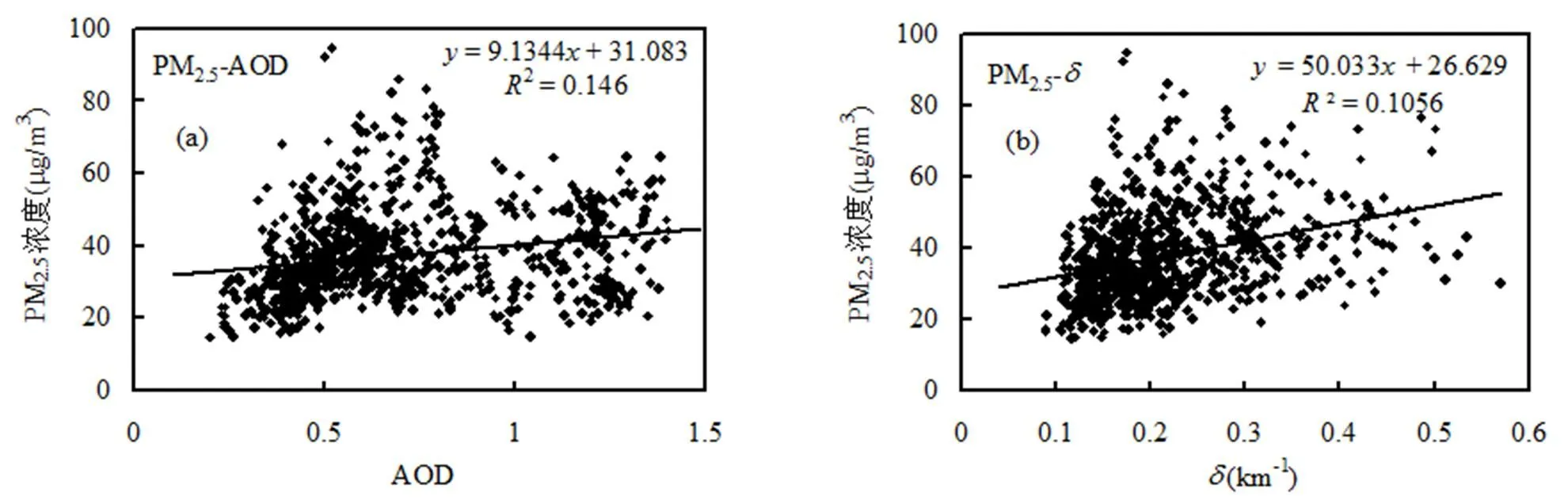
2.2 模型擬合結果

在進行數據質量控制后,得到990個PM2.5- AOD有效數據,采用旬平均AOD、、RH、WS、PBLH、NDVI等6個要素作為自變量,建立地表PM2.5濃度的LME模型,模型擬合精度較高(圖4),2為0.711,RMSE為7.4μg/m3,MAE為4.856μg/m3.由圖4可以看出,PM2.5濃度主要集中在10~60μg/m3,而LME模型在PM2.5濃度小于35μg/m3時較多呈現高估,而高于35μg/m3時則較多為低估,但從總體上看高估、低估的現象并不明顯,說明LME模型能夠比較好的模擬旬平均PM2.5濃度的時空變化.

表1為旬平均LME擬合模型的固定效應參數,模型中的所有自變量都通過了顯著性檢驗(值<0.01),模型中AOD的固定斜率1為26.834、的固定斜率2為3.945,均為正值,表明AOD、與PM2.5呈現正相關關系,RH、WS、PBLH、NDVI等4個因子的固定斜率3~6分別為-0.644、-8.846、-0.018、-4.835,均為負數,表明RH、WS、PBLH、NDVI與PM2.5呈現負相關關系,與前述簡單的線性相關分析結果相一致.值得注意的是,與PM2.5線性相關分析中的2較RH、PBLH、NDVI等3個因子的都要大些(2越大相關性強),而LME模型中對應的值較RH、PBLH、NDVI的都要大(越大相關性越弱),這與LME模型中引入逐旬隨機參數b有關.

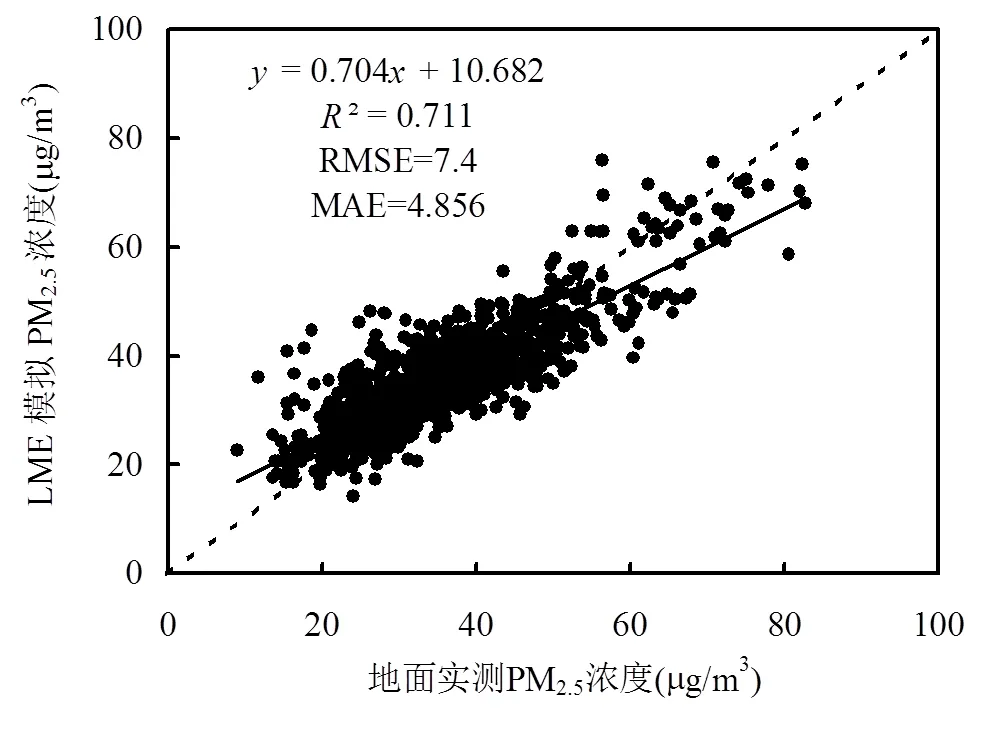
圖4 LME 模型擬合結果

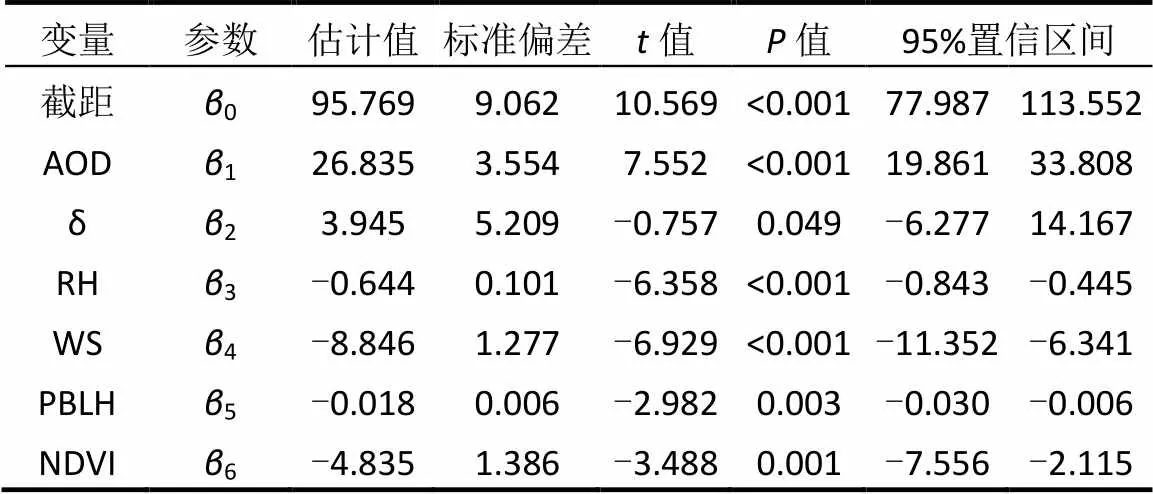
表1 LME模型固定效應參數

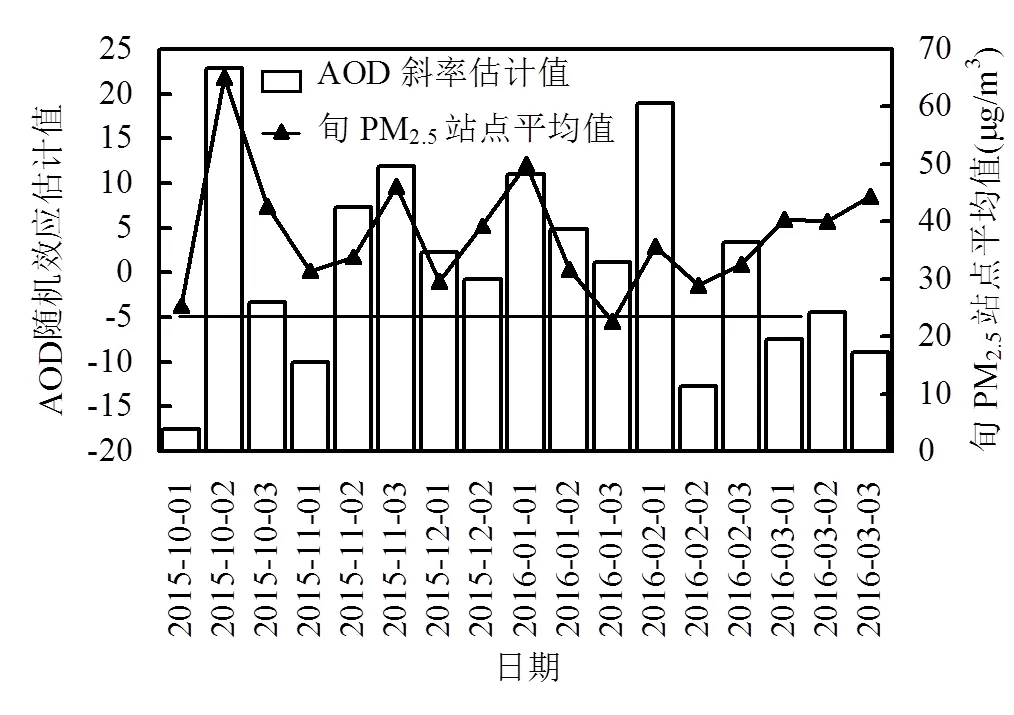
圖5 2015年10月~2016年3月逐旬LME隨機參數bi及PM2.5站點平均值

LME模型中AOD的逐旬隨機截距b及PM2.5平均值如圖5所示,可以看出隨機截距b及PM2.5之間有一定的正相關關系,這種共變趨勢在2015年10月比較明顯,上旬至下旬的隨機效應的AOD斜率與逐旬PM2.5站點平均值都呈現先大幅上升后下降的變化趨勢;另外AOD的隨機斜率的最大值為22.82,最小值為-17.52,從其較大幅度的正負變化表明AOD-PM2.5的關系隨時間不同會有明顯的變化.

3.3 模型交叉驗證結果

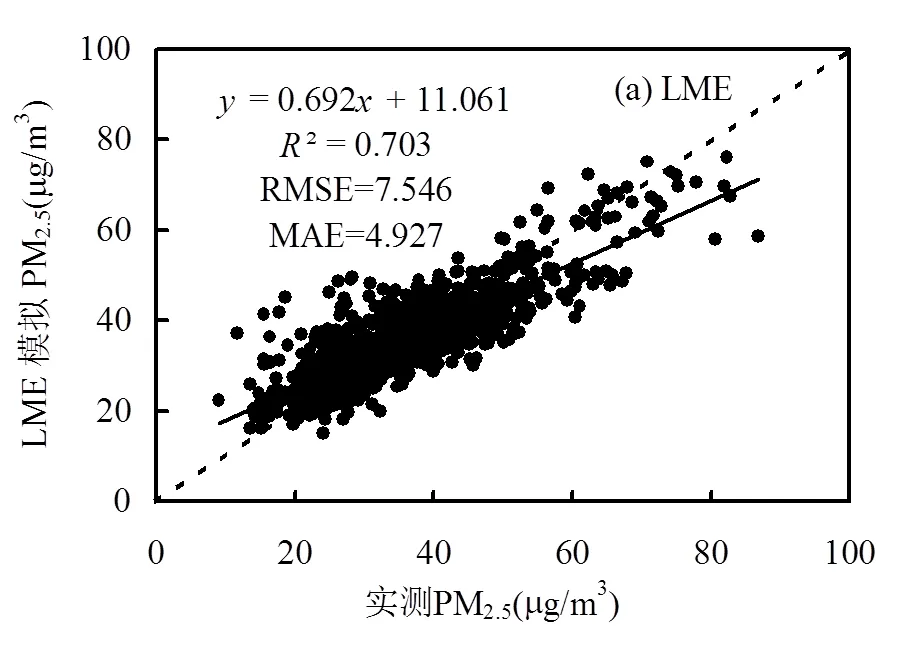
圖6為LME模型及LME+BME模型交叉驗證結果,LME模型的交叉驗證2為0.703,RMSE為7.546μg/m3,MAE為4.927μg/m3.LME+BME模型模擬結果(圖6b),驗證精度較僅使用LME有一定程度的提高,RMSE及MAE有所下降(圖6a),2為0.751, RMSE為6.886μg/m3,MAE為4.52μg/m3,交叉驗證結果表明LME模型模擬結果結合BME后能夠一定程度上減輕低值高估、高值低估的現象,即更好地解釋珠江三角洲地區旬平均PM2.5濃度的時空分布.

3.4 2015年10月中旬反演結果分析

前述2015年10月中旬為地面實測PM2.5濃度旬平均最高值,本文以此旬為例,首先通過AOD等6個模型自變量的空間分布情況,分析此旬PM2.5出現高值的原因,并比較地面實測PM2.5克里金結果、LME模型模擬PM2.5分布及LME結合BME模擬得到的PM2.5空間分布的差異,以比較兩模型模擬結果的精度.

圖7 2015年10月中旬LME模型自變量空間分布

(a) AOD, (b), (c) RH, (d) WS, (e) PBLH, (f) NDVI

圖8 2015年10月中旬PM2.5 模型模擬與實測結果分布

(a) 實測 PM2.5站點分布, (b) 經克里金插值的PM2.5分布,(c) LME模擬PM2.5分布, (d) LME+BME模擬PM2.5分布

圖9 2015年10月~2016年3月LME+BME模型模擬逐旬PM2.5濃度空間分布

圖7為2015年10月中旬AOD及輔助數據的空間分布,可以看出AOD與的分布相同,與NDVI、RH相反,AOD和高值集中于佛山、東莞及中山市等地區,而NDVI、RH在這些地區則為低值,說明與AOD為比較明顯的正相關關系而NDVI、RH與AOD為比較明顯的負相關關系;而WS和PBLH在此旬整體呈現較低值,說明當二者處于低值時,此種天氣狀況不利于PM2.5的擴散,是該時間段污染的原因.

2015年10月中旬LME模型公式參數如下:

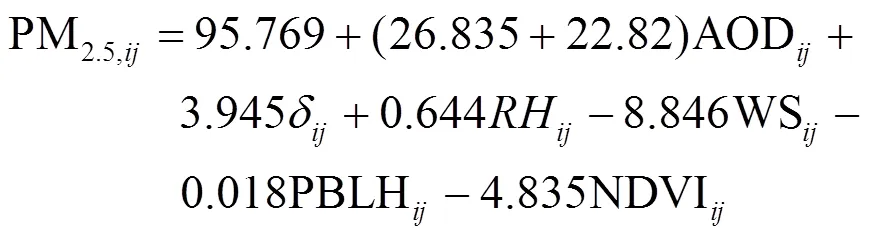
地面實測PM2.5克里金插值由于PM2.5站點分布不均勻(圖8 (a)),肇慶市以及江門市得到的克里金插值結果與鄰近站點相類似,但從插值結果(圖8(b))可以看出PM2.5濃度較大的區域集中在珠江三角洲中部地區,主要為佛山市和中山市,對比圖9 (c)、(d)的模型模擬結果,BME融合結果(圖8(d))相較于僅使用LME模型的結果(圖8(c))能夠更好地體現這一污染分布特點.但兩種模擬結果在佛山市的中部地區,濃度較地面實測數據克里金結果偏小,反映了模擬結果對于旬平均PM2.5代表性的不足.

3.5 2015年10月~2016年3月PM2.5濃度空間分布模擬

圖9為2015年10月~2016年3月LME+BME模型模擬旬平均PM2.5濃度空間分布圖.由圖9可以看出:空間尺度上,PM2.5濃度的分布有明顯的區域特征,高污染區域主要集中于廣州、佛山、東莞、中山等中部地區,說明這些經濟發達且高度城市化的城市是珠江三角洲污染源所在地,高濃度PM2.5產生于此并不斷向四周擴散至肇慶、惠州、江門等地,使總體PM2.5濃度呈現出由中部地區向周圍城市梯度下降的趨勢.

時間尺度上,PM2.5濃度比較高的旬為2015年10月中/下旬、2015年12月下旬以及2016年3月下旬.其中2015年10月中旬為空氣質量最差的旬,污染較嚴重的中山、佛山等地PM2.5濃度達到80μg/m3,東莞、深圳以及江門、惠州的部分區PM2.5濃度均超過了60μg/m3;而2015年10月上旬、2015年12月上旬以及2016年1月下旬則為PM2.5濃度較低的旬,當PM2.5濃度較低時,其空間分布沒有明顯規律,即沒有表現出由高濃度區域向四周梯度下降的趨勢,其中2016年1月下旬則PM2.5濃度最低,大部分地區低于20μg/m3,僅肇慶和廣州、佛山的部分地區在20~30μg/m3.從PM2.5濃度的時空變化上,2015年10月~2016年1月表現出兩個比較明顯的污染過程:2015年10月上旬空氣質量較好,而到10月中旬PM2.5濃度突然上升達到峰值,局部地區超過80μg/m3,而后一直到2015年12月上旬PM2.5濃度處于逐漸下降的趨勢,污染區域在不斷縮小,之后又慢慢上升至2015年12月下旬達到峰值,在這之后到2016年1月下旬達到谷值.由PM2.5濃度變化速率可以看出,其由較低值上升至下降前的峰值可以非常快,而下降相較于上升的速率是比較緩慢的,表明PM2.5顆粒物的聚集速率遠遠高于擴散速率.

3 討論

通過使用最新的MODIS 3km AOD產品估算了高精度的地面PM2.5濃度,為珠江三角洲地區大氣污染防治提供了更詳細的空間信息.以往基于AOD的珠江三角洲地區PM2.5估算研究中大多使用MODIS 10km AOD產品[28-29],同時有研究[30]發現,對中國地區而言,使用不同的反演模型或者在模型中加入氣象因子等都沒有使用高分辨率AOD對反演結果的影響大,充分說明了使用高分辨率AOD進行PM2.5反演的優越性.

以旬為時間單位,對旬平均PM2.5濃度進行遙感反演.而以往研究中往往以日、月、年為時間單位進行PM2.5濃度的估算,因珠江三角洲地區降雨較多,AOD缺失問題較其他地區嚴重,難以獲取連續分布的AOD數據,即以日為時間單位無法反演得到連續的PM2.5空間分布情況;而以月或年為時間單位,則無法反映PM2.5在較短時間內空間上的變化.以旬為單位則可以保證得到時空連續的PM2.5分布情況又不至于損失太多時間上的變化信息,以期為珠江三角洲地區大氣污染防治提供更好的參考.

采用雙層模型,將LME與BME結合起來,以更好地模擬PM2.5-AOD關系在空間和時間上的變化,并在此基礎上引入氣象因子作為輔助自變量,以提高模型模擬精度.LME模型包含的隨旬變化的隨機斜率,可以反映PM2.5-AOD關系在時間上的變化,而BME模型通過結合地面實測PM2.5濃度以及LME預測值,能夠有效地捕捉PM2.5空間上的變化.

PM2.5在時間以及空間上受到多種因素的影響,本文僅納入氣象因子而并未納入污染源、土地利用數據,在后續的研究中考慮加入其它影響因子以提高模型模擬精度.

4 結論

4.1 在旬尺度上分析PM2.5與環境因子的相關關系,結果表明旬平均AOD及與PM2.5呈較明顯的正相關關系,而與其他氣象因子(RH、WS、PBLH、NDVI)呈負相關關系,說明AOD可以反映PM2.5的空間分布,加入其他環境因子可以提升PM2.5模擬結果.

4.2 基于LME模型的結果以及BME模型,估算了珠江三角洲地區2015年10月~2016年3月的旬平均PM2.5濃度分布.結果顯示,空間上,PM2.5高濃度地區主要集中在廣州、佛山、東莞等地區;低濃度地區主要集中在肇慶、惠州、江門的南部等地區;時間上,PM2.5濃度在2015年10月中旬及2015年12月下旬兩次達到峰值,且由較低值上升至下降前的峰值可以非常快,而下降相較于上升的速率是比較緩慢的,表明PM2.5顆粒物的聚集速率遠遠高于擴散速率.

[1] Yang Y, Christakos G, Huang W, et al. Uncertainty assessment of PM2.5contamination mapping using spatiotemporal sequential indicator simulations and multi-temporal monitoring data [J]. Science Reports, 2016,6:24-35.

[2] Zou B, Luo Y Q, Wan N, et al. Performance comparison of LUR and OK in PM2.5concentration mapping: a multidimensional perspective [J]. Science Reports, 2015,5:86-98.

[3] Lv B, Hu Y, Chang H H, et al. Improving the accuracy of daily PM2.5distributions derived from the fusion of ground-level measurements with aerosol optical depth observations, a case study in north China [J]. Environment Science & Technology, 2016,50(9): 4752-4759.

[4] Zhang W, Capps S L, Hu Y, et al. Development of the high-order decoupled direct method in three dimensions for particulate matter: enabling advanced sensitivity analysis in air quality models [J]. Geoscientific Model Development Discussions, 2011,4(4):355-368.

[5] Engel-Cox J A., Holloman C H., Coutant B W, et al. Qualitative andquantitative evaluation of MODIS satellite sensor data for regional and urban scaleair quality [J]. Atmospheric Environment, 2004,38: 2495–2509.

[6] Engel-Cox J A., Young G S, Hoff R M. Application of satellite remote-sensingdata for source analysis of ?ne particulate matter transport events [J]. Journal of the Air &Waste Management Association, 2005,55:1389–1397.

[7] Bucher H U, Baumgartner R, Bucher N, et al. A review of land-use regression models to assess spatial variation of outdoor air pollution [J]. Atmospheric Environment, 2008,42(33):7561-7578.

[8] Kloog I, Chudnovsky A A, Just A C, et al. A new hybrid spatio- temporal model for estimating daily multi-year PM2.5, concentrations across northeastern USA using high resolution aerosol optical depth data [J]. Atmospheric Environment, 2014,95(1):581-590.

[9] Wu J S, Li J C, Peng J, et al. Applying land use regression model to estimate spatial variation of PM2.5in Beijing,China [J].Environmental Science Pollution Research, 2015,22(9):7045-7061.

[10] Hu Z Y. Spatial analysis of MODIS aerosol optical depth, PM2.5, and chronic coronary heart disease [J]. International Journal of Health Geographics, 2009,8(1):27.

[11] Ma Z, Hu X, Huang L, et al. Estimating ground-level PM2.5in China using satellite remote sensing [J]. Environmental Science & Technology, 2014,48(13):7436.

[12] Song W, Jia H, Huang J, et al. A satellite-based geographically weighted regression model for regional PM2.5, estimation over the Pearl River Delta region in China [J]. Remote Sensing of Environment, 2014,154:1-7.

[13] 張 瑩,李正強.利用細模態氣溶膠光學厚度估計PM2.5[J]. 遙感學報, 2013,17(4):929-943. Zhang Y, Li Z Q. Estimation of PM2.5from fine-mode aerosol optical depth [J]. Journal of Remote Sensing, 2013,17(4):929-943.

[14] Zhang Y, Li Z .Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation [J]. Remote Sensing of Environment, 2015,160:252-262.

[15] Lin C, Li Y, Yuan Z, et al. Using satellite remote sensing data to estimate the high-resolution distribution of ground-level PM2.5[J]. Remote Sensing of Environment, 2015,156:117-128.

[16] Li Z Q, Zhang Y, Shao J, et al. Remote sensing of atmospheric particulate mass of dry PM2.5near the ground: Method validation using ground-based measurements [J]. Remote Sensing of Environment, 2016,173:59-68.

[17] Lee H J, Liu Y, Coull B A, et al. A novel calibration approach of MODIS AOD data to predict PM2.5concentrations [J]. Atmospheric Chemistry and Physics, 2011(11):7991-8002.

[18] Lee H J, Coull B A, Bell M L, et al. Use of satellite-based aerosol optical depth and spatial clustering to predict ambient PM2.5concentrations [J]. Environmental Research, 2012,(118):8-15.

[19] Kloog I, Chudnovsky A A, Just A C, et al. A new hybrid spatio-temporal model for estimating daily multi-year PM2.5concentrations across northeastern USA using high resolution aerosol optical depth data [J]. Atmospheric Environment, 2014,95(1):581-590.

[20] Zheng Y X, Zhang Q, Liu Y, et al. Estimating ground-level PM2.5concentrations over three megalopolises in China using satellite-derived aerosol optical depth measurements [J]. Atmospheric Environment, 2016,124:232-242.

[21] Xie Y, Wang Y, Zhang K, et al. Daily estimation of ground-level PM2.5concentrations over Beijing using 3km resolution MODIS AOD[J]. Environmental Science & Technology, 2015,49(20):12280-12288.

[22] Ma Z W, Liu Y, Zhao Q Y, et al. Satellite-derived high resolution PM2.5concentrations in Yangtze River Delta Region of China using improved linear mixed effects model [J]. Atmospheric Environment, 2016,133:156-164.

[23] Yu H L, Wang C H, Liu M C, et al. Estimation of fine particulate matter in Taipei using landuse regression and bayesian maximum entropy methods [J]. International Journal of Environmental Research & Public Health, 2011,8(6):2153-2169.

[24] Beckerman B S, Jerrett M, Serre M, et al. A hybrid approach to estimating national scale spatiotemporal variability of PM2.5in the contiguous united states [J]. Environmental Science & Technology, 2013,47(13):7233-7241.

[25] 江曲圖,何俊昱,王占山,等.基于LUR/BME的海岸帶地區PM2.5時空特性研究 [J]. 中國環境科學, 2017,37(2):424-431. Jiang Q T, He J Y, Wang Z S, et al. Spatiotemporal analysis of PM2.5in large coastal domains by combining Land Use Regression and Bayesian Maximum Entropy [J]. China Environmental Science, 2017, 37(2):424-431.

[26] Christakos G. A Bayesian maximum-entropy view to the spatial estimation problem [J]. Mathematical Geosciences, 1990,22(7):763- 777.

[27] 楊 勇,張若兮.貝葉斯最大熵地統計方法研究與應用進展[J]. 土壤, 2014,(3):402-406. Yang Y, Zhang R X. Review on bayesian maximum entropy geostatistics method [J]. Soils, 2014,(3):402-406.

[28] Song W, Jia H, Huang J, et al. A satellite-based geographically weighted regression model for regional PM2.5, estimation over the Pearl River Delta region in China [J]. Remote Sensing of Environment, 2014,154:1-7.

[29] Zheng Y, Zhang Q, Liu Y, et al. Estimating ground-level PM2.5concentrations over three megalopolises in China using satellite- derived aerosol optical depth measurements[C]//EGU General Assembly Conference. EGU General Assembly Conference Abstracts, 2016.

[30] 吳健生,王 茜,李嘉誠,等.PM2.5濃度空間分異模擬模型對比:以京津冀地區為例[J]. 環境科學, 2017,38(6):2191-2201. Wu J S, Wang X, Li J C, et al. Comparison of models on spatial variation of PM2.5concentration: A case of Beijing-Tianjin-Hebei region [J]. Environmental Science, 2017,38(6):2191-2201.

Fusion of satellite data and ground observed PM2.5in Pearl River Delta region with linear mixed effect and Bayesian maximum entropy method.

ZHOU Shuang1,2, WANG Chun-lin2,3*, SUN Rui1, TANG Jing3, HUANG Jun3, SHEN Zi-qi3

(1.State Key Laboratory of Remote Sensing Science, Faculty of Geographical Science, Beijing Normal University, Beijing 100875, China；2.Guangzhou Institute of Tropical and Marine of Meteorology, Guangzhou 510640, China；3.Guangzhou Climate and Agrometeorology Center, Guangzhou 511430, China)., 2019,39(5)：1869~1878

By combining Linear Mixed Effect (LME) model and Bayesian Maximum Entropy (BME) method, ground-level PM2.5from October 2015 to March 2016 in Pearl River Delta region were estimated in this paper by AOD, NDVI and meteorological data. The results showed that the prediction accuracy of LME+BME method were greatly improved compared with that of the LME method. The cross-validation2of LME+BME model was 0.751, and root mean squared prediction error (RMSE) was 6.886μg/m3, the mean prediction error (MPE) was 4.52μg/m3, while2=0.703, RMSE=7.546μg/m3, and MAE=4.927μg/m3for the LME method. The high PM2.5concentration was mainly located in Guangzhou, Foshan, Dongguan, and the low PM2.5concentration was mainly distributed in Zhaoqing, Huizhou, Jiangmen. In terms of seasonal variation, PM2.5pollution was more serious in mid-October in 2015, late November in 2015 and late March in 2016, while it was relatively low in early October in 2015, early December in 2015 and late January in 2016.

PM2.5；MODIS AOD；linear mixed-effect model；Bayesian maximum entropy；Pearl River Delta region

X513

A

1000-6923(2019)05-1869-10

周 爽(1993-),女,遼寧沈陽人,北京師范大學碩士研究生,主要從事大氣環境遙感研究.發表論文1篇.

2018-10-16

國家重點研發計劃(2016YFC02033305,2016YFC0201901);廣州市科技計劃項目(201604020028)

*責任作者, 研究員, 13610213085@qq.com