基于Monte Carlo模擬的河流水質評價——以溫瑞塘河為例

黃 宏,商 栩,梅 琨,王振峰,夏 芳,黃樹輝,張明華,紀曉亮*

?

基于Monte Carlo模擬的河流水質評價——以溫瑞塘河為例

黃 宏1,2,3,商 栩1,2,3,梅 琨1,2,3,王振峰1,2,3,夏 芳1,2,3,黃樹輝1,張明華1,2,3,紀曉亮1,2,3*

(1.溫州醫科大學公共衛生與管理學院,浙江 溫州 325035；2.浙江省流域水環境與健康風險研究重點實驗室,浙江 溫州 325035；3.浙南水科學研究院,浙江 溫州 325035)

基于水質評價的綜合污染指數(CWQI)法和水質指標實測含量的統計分析,應用Monte Carlo模擬方法,建立了河流水質評價的Monte Carlo- CWQI耦合模型并進行實例研究.通過建立的耦合模型和溫瑞塘河流域14個監測斷面2004~2010年的水質監測數據,定量分析各監測斷面隸屬于不同污染等級的概率水平和各水質指標對水體污染的影響程度.結果表明:溫瑞塘河水系水質污染十分嚴重,勤奮、九山、東水廠、十字河、南白象、灰橋、新橋、米篩橋、仙門、光明、郭溪、瞿溪、西岙和梧田監測斷面處于重度污染的概率分別為28.50%,0.55%,92.71%,59.73%,78.85%,39.38%,78.87%,83.09%,65.32%,78.08%, 0.00%,0.96%,68.09%,86.06%;處于嚴重污染的概率分別為71.28%,0.01%,4.33%,39.76%,21.07%,60.59%,4.42%,12.41%,11.02%,21.24%,0.00%,0.02%,1.42%, 13.12%.各監測斷面總氮(TN),氨氮(NH3-N)和溶解氧(DO)的Spearman等級相關系數范圍分別是0.41~0.76、0.25~0.63和0.14~0.66,是其他指標的2倍以上,表明影響該地區水質達標的主要因子是TN,NH3-N和DO.本研究拓寬了河流水質評價的研究視角,能夠為流域水環境管理提供豐富的決策依據.

Monte Carlo模擬；水質評價；不確定性；溫瑞塘河

近年來,隨著社會經濟的快速發展和城市化進程的加快,越來越多的工業、生活和農業排放物進入到河流中,導致河流水質污染和惡化,水資源需求與供給之間的矛盾不斷加劇[1-4].流域水環境管理和治理的重要基礎性工作是明晰河流水體環境質量[5-6].

水質評價是指通過對水體化學、物理和生物指標的監測和調查,根據不同的目的和要求,使用一定的方法對水體污染程度進行的定量描述[7].常見的水質評價方法主要包括單因子指標法、綜合污染指數(CWQI)法、模糊綜合評價法、水質標識指數法、投影尋蹤法、人工神經網絡和支持向量機方法等[8-15].鑒于環境系統的復雜性,以上各種水質評價方法在實際應用中各有利弊.由于計算簡單,易于操作,綜合性和可比性強,能夠反映水質現狀是否滿足水功能區要求,CWQI法是目前國內外普遍采用的一種水質評價方法[12,16-17].然而,CWQI法等常規水質評價方法是從確定性的角度根據一次或多次采樣的均值對研究水體進行質量評價,只能反映研究對象的總體污染情況,難以揭示其真實的污染程度,不利于全面、深入的了解水體環境質量狀況.在水質監測工作中,自然因素的隨機變化(如徑流量變化,降雨事件等)和人為因素的影響(如采樣和測量誤差等)會導致水體污染物的濃度存在不確定性[18].因此,水質評價結果的不確定性難以避免,只有充分考慮水質評價中的不確定性,才能獲得準確的評價結果,為決策者提供全面的信息.

不確定性是當前水環境研究領域的前沿和難點問題.蒙特卡羅(Monte Carlo)模擬是解決不確定性問題最為有效的工具之一[19-20].Monte Carlo模擬是一種通過隨機抽樣對模型或數學方程進行求解的分析方法,屬于計算數學的一個分支[21].該方法能夠比較逼真地描述事物的特點及物理實驗過程,解決一些數值方法難以解決的問題,很少受幾何條件限制,收斂速度與問題的維數無關.對于那些受客觀條件限制而難以進行的試驗而言,是一種極好的替代方法.并且,可以給出每種結果的概率,能夠為決策者提供更多的信息,降低決策風險[22].近年來, Monte Carlo方法已經在水環境模擬模型的不確定性分析、參數估算和環境污染物健康風險評價等研究中得到了廣泛的應用[18,23-24].但是,尚鮮見Monte Carlo方法應用于水體質量評價不確定性分析的相關研究報道.

本文嘗試將Monte Carlo模擬應用到水體質量評價中,結合CWQI法,建立了基于不確定性理論的Monte Carlo-CWQI耦合模型.以中國東南沿海地區典型平原河網-溫瑞塘河流域為研究區域,對其水系污染現狀進行綜合評價,以期為流域水污染的防控和水資源的合理開發利用提供科學依據.

1 材料與方法

1.1 研究區域

圖1 溫瑞塘河流域水質監測點位置

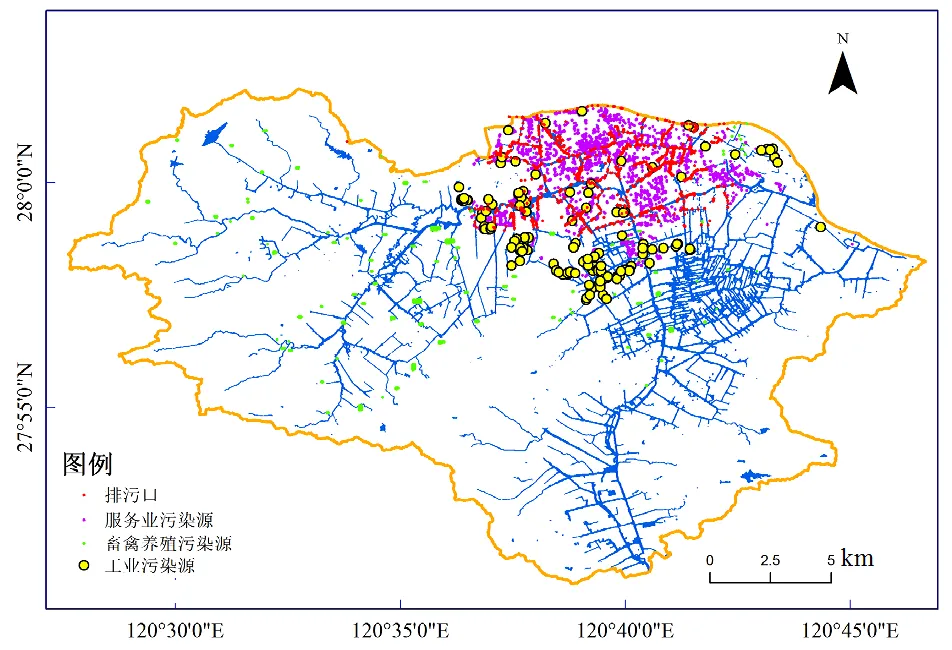
圖2 溫瑞塘河流域污染源分布

包括整個流域的畜禽養殖污染源和城區的排污口、服務業污染源及工業污染源

本文選取位于浙江省溫州市的溫瑞塘河流域為研究區域,其地理位置介于120°27′47.3″E~ 120°47′45.3″E和29°20′2.4″N~29°42′37.5″N之間(圖1).溫瑞塘河發源于溫州西部山區,總體流向為自西向東流經溫州城區,隨后自北向南,流經城鄉結合區及農業種植區,之后在瑞安匯入飛云江,最后流入東海.流域面積740km2,水面面積22km2,蓄水量6.5′107m2,水系河網總長度1178.4km,其中主河道長33.8km.該區屬亞熱帶海洋性季風氣候,年均溫度17.9℃,年均降雨量1800mm,70%的降雨集中在4~9月.作為典型的南方平原河網,溫瑞塘河河道縱橫交錯,河水與河床的比降相當小甚至接近于零,河流流向不定,流速十分緩慢,水質不均勻.

溫瑞塘河流域為東南沿海地區典型的平原河網,各種排污口和污染源密布(圖2).自20世紀80年代以來,由于大量未經處理的工業、生活及農業廢水排放入河,造成水質嚴重惡化,制約了當地的經濟和社會發展.

1.2 數據

溫瑞塘河流域2004~2010年水質數據由溫州市環保局提供,其水質監測頻率為兩月一次.監測斷面包括勤奮、九山、東水廠、十字河、南白象、灰橋、新橋、米篩橋、仙門、光明、郭溪、瞿溪、西岙和梧田(圖1).選擇溶解氧(DO)、高錳酸鹽指數(CODMn)、五日生化需氧量(BOD5)、氨氮(NH3-N)、總磷(TP)、總氮(TN)、石油類(Petrol)和氟化物(F)8項作為評價指標.水質指標根據《水和廢水監測分析方法》[25]規定的方法進行分析測定.對水體質量的評價參考國家《地表水環境質量標準》(GB3838– 2002)[26].

1.3 Monte Carlo-CWQI耦合模型

1.3.1 水質評價的CWQI法 CWQI法是對各污染指標的相對污染指數進行統計,得出代表水體污染程度的數值,該方法用以確定污染程度和主要污染物,并對水污染狀況進行綜合判斷.根據如下公式進行CWQI的計算:

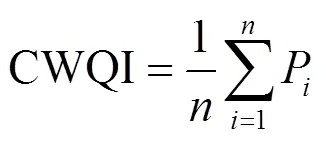
式中:CWQI為綜合污染指數;為參與評價的水質指標個數;P為單因子污染指數,數值越大,表明該因子的污染程度越高.

對于非DO指標的計算公式如下:

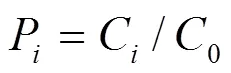
由于DO為高優指標,即數值越高代表水質越好,故采用倒數變換的方式將其轉化為低優指標.DO指標的計算公式如下:

式中:C為水質指標的實測值;0為指標的標準值,根據《浙江省水功能區、水環境功能區劃分方案》[27],溫瑞塘河流域以地表水環境質量標準中V類水質標準進行控制.

計算出CWQI后,可根據污染分級標準劃定水質等級.CWQI越大,污染越重:CWQI￡0.4,說明水質未受到污染,狀況較好,屬清潔水體;0.42時,水質污染非常嚴重[28].

1.3.2 Monte Carlo方法原理 Monte Carlo方法的理論基礎是概率統計,手段是隨機抽樣,基本思想是當所要求解的問題是某個隨機變量的期望值或者是某種事件出現的概率時,可以通過某種“試驗”的方法,得到這個隨機變數的平均值或者這個事件出現的頻率,并將它們作為問題的解[29].Monte Carlo模擬步驟包括:(1)根據提出的問題構造概率分布模型,使問題的解對應于該模型中隨機變量的某些特征(如概率、均值和方差等);(2)確定參數的概率分布;(3)根據參數的分布,利用給定的某種規則,進行大量的隨機抽樣;(4)對隨機抽樣的數據進行必要的數學計算,統計分析模擬試驗結果,得出相應的結論.

1.3.3 Monte Carlo-CWQI耦合模型構建方法 對公式(1)進行編輯,以CWQI為目標變量,設置8個隨機變量,分別為各評價指標的單因子污染指數,從隨機變量的概率分布中進行30000次Monte Carlo抽樣(置信水平:95%;抽樣方法:拉丁超立方抽樣).將每一次抽樣得到的隨機變量帶入式(1)進行模擬,從而獲得30000個結果,代表了各水質指標參數不確定條件下所有可能得到的結果.此基礎上,為表征各水質指標對水體污染程度的影響,利用Crystal Ball自帶的模型參數靈敏度分析功能,計算了各水質指標的Spearman等級相關系數(SRCC):

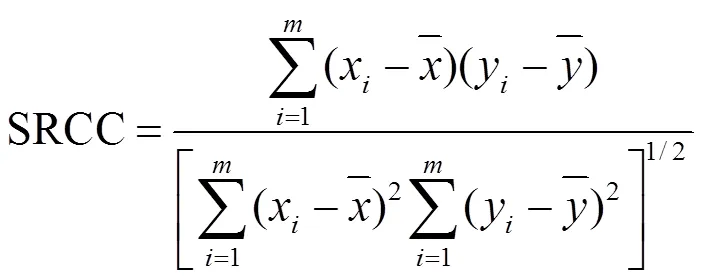
式中:是模擬次數;是輸入參數的排序值;是輸出結果的排序值.SRCC的取值范圍在-1~1之間.SRCC為負值,表示輸入變量與目標變量呈負相關,為SRCC正值,表示目標變量與目標變量呈正相關; SRCC的絕對值越高,說明輸入變量對目標變量的影響程度越大.通常,當輸入參數的SRCC絕對值大于0.5時,說明其和目標變量之間有本質的相關性[30].

1.4 數據處理與圖形制作

通過Minitab軟件運行樣本擬合優度的Anderson-Darling檢驗;應用基于Microsoft Excel環境的Crystal Ball 11軟件實現CWQI的Monte Carlo模擬及不同污染指標的靈敏度分析;其余統計分析利用SPSS 17軟件完成;采用ArcGIS 10.2和Origin Pro 9.0軟件制作相關圖件.

2 結果與討論

2.1 河流水質指標描述性統計分析

溫瑞塘河流域不同監測斷面水質指標的時間變化見圖3.TN濃度變化范圍為0.38~25.30mg/L,平均濃度遠超目標水質限值,是V類水標準的3.66倍.NH3-N是主要的氮素形態,占TN含量的80%以上.TP平均濃度為0.46mg/L,劣于V類水質標準.DO濃度在0.04~10.80mg/L的范圍內變化,約60%的樣本濃度低于2mg/L.CODMn和BOD5的平均濃度分別為5.97,6.97mg/L,處于III類和V類水質標準.約50%的樣本Petrol濃度低于檢測限濃度,其濃度變化區間為0.05~1.24mg/L.水體中F含量很低,平均值0.45mg/L,為I類標準.

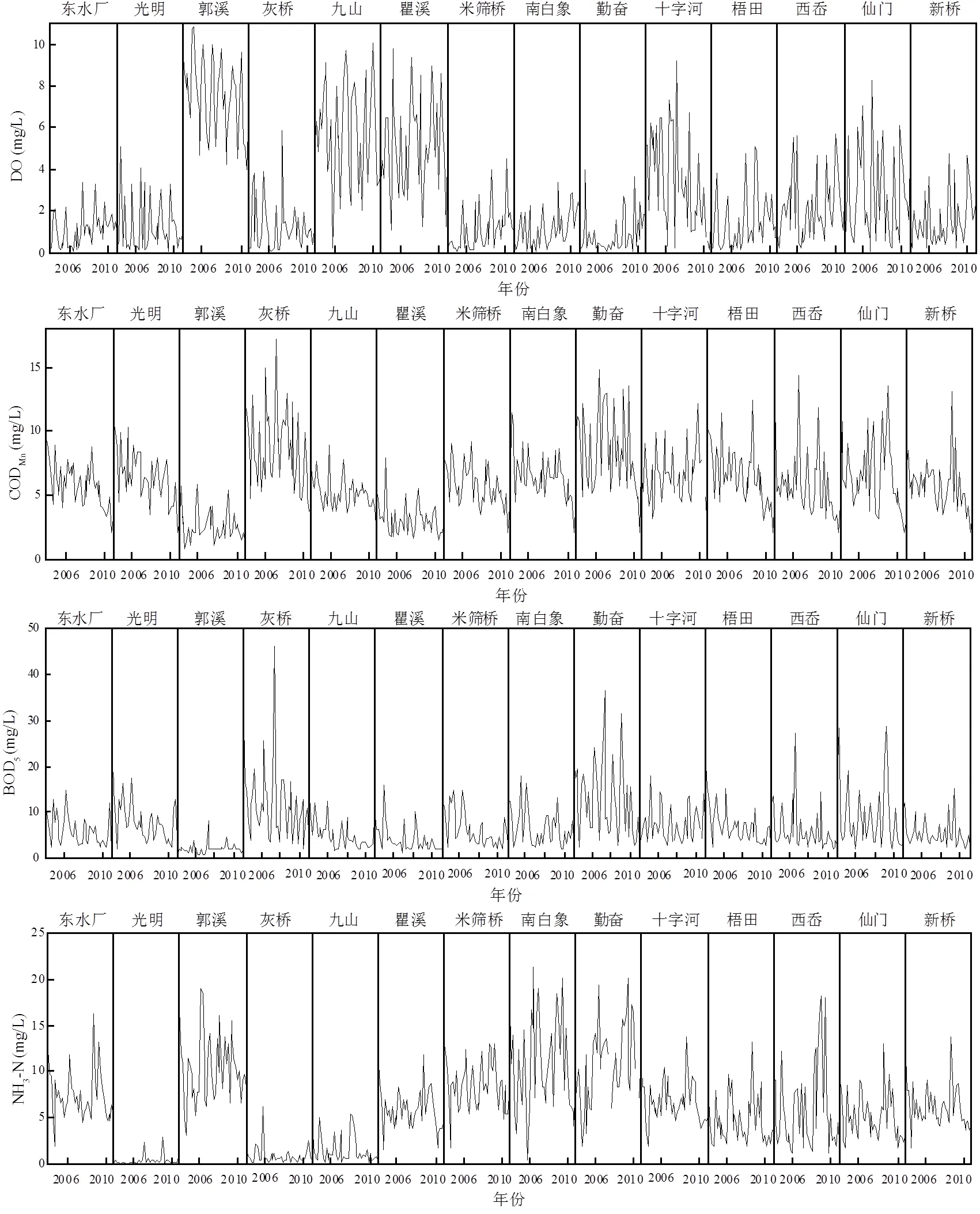
2.2 模型輸入參數的概率分布

確定模型輸入參數的概率分布類型和分布參數是Monte Carlo模擬中最為重要的步驟.計算出各水質指標單因子污染指數后,為保證后期模型模擬結果的準確性,采用常用對數變換的方式對數據進行處理.依據對數函數的性質,單因子污染指數數值小于1的,取對數后為負值,反之,則為正值.由于DO和Petrol指標存在大量低于檢測限的數據,為使參數的最終分布符合實際情況,故低于檢測限的數據不參與參數的概率分布擬合.自然對數變換后的水質指標單因子污染指數首先經Kolmogorov-Smirnov檢驗判斷是否服從正態分布.對于不服從正態分布的指標,應用擬合優度的Anderson-Darling檢驗確定其最優擬合分布.經檢驗,除瞿溪監測點F最優的擬合分布為最大極值分布外,其余站點各指標的擬合分布都符合正態分布.在Crystal Ball中利用各指標的分布參數(正態分布為均值和標準差;最大極值分布為位置和尺度參數)以生成服從相應概率分布的隨機數.

2.3 溫瑞塘河流域水質評價

根據CWQI的Monte Carlo模擬結果,歸納統計30000次模型模擬得到的CWQI,可以得到溫瑞塘河流域不同監測斷面CWQI的概率分布(表1).流域內14個監測斷面的實際計算結果都在該范圍之內,表明模擬結果真實可信.

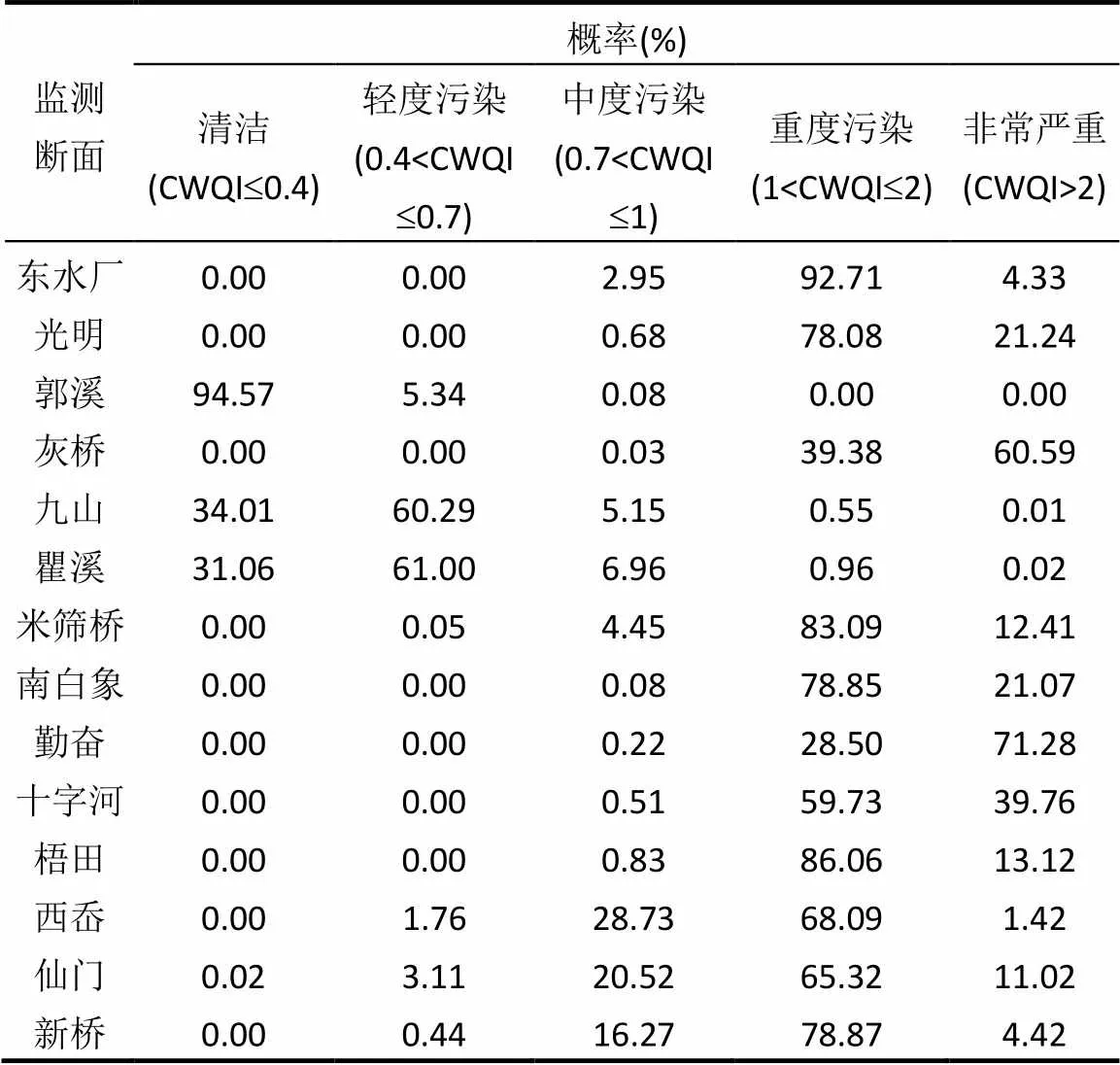
表1 不同監測斷面處于各污染程度等級的概率

根據模型模擬得到的CWQI值和污染等級判別標準,可以得到不同監測斷面隸屬于每個污染等級的概率水平.溫瑞塘河水系水質污染十分嚴重,勤奮、九山、東水廠、十字河、南白象、灰橋、新橋、米篩橋、仙門、光明、郭溪、瞿溪、西岙和梧田監測斷面處于重度污染的概率分別為28.50%, 0.55%, 92.71%, 59.73%, 78.85%, 39.38%, 78.87%, 83.09%, 65.32%, 78.08%, 0.00%, 0.96%, 68.09%, 86.06%;處于嚴重污染的概率分別為71.28%, 0.01%, 4.33%, 39.76%, 21.07%, 60.59%, 4.42%, 12.41%, 11.02%, 21.24%, 0.00%, 0.02%, 1.42%,13.12%;處于或優于輕度污染的概率分別為0.22%, 99.44%, 2.96%, 0.51%, 0.08%, 0.03%, 16.71%, 4.50%, 23.66%, 0.68%, 100.00%, 99.02%, 30.49%, 0.83%.水質評價是一種利用多種信息推斷出各種水質類別的可能性,以可能性最大作為依據,進行最終決策的過程[31].根據最大隸屬度原則,勤奮、灰橋、九山、瞿溪和郭溪水質類別分別為嚴重污染、嚴重污染、輕度污染、輕度污染和清潔;其余斷面水質類別都為重度污染.

圖4 溫瑞塘河水質的空間變化

由于溫瑞塘河不同類型河道納污強度的差異和水體中污染物遷移轉化過程的不同,水系污染程度呈現顯著的空間異質性(圖4).灰橋、勤奮、十字河位于城區深入居民區的支流上,周圍廣泛分布著排污口,大量未經處理的城市生活污水直排入河.更為嚴重的是,這些支流小而狹窄,河流流速非常緩慢甚至滯留,河道中累積的污染物無法及時擴散,導致其聚集,污染最嚴重.相較而言,東水廠和光明監測斷面水體流動性強于灰橋、勤奮、十字河斷面,因此污染程度相對較輕.九山監測斷面位于水上娛樂運動河段,水體質量受到嚴格保護,因此水質隸屬于輕度污染.主河道水體流動相對較快,有利于河道中污染物的轉移和自凈.河網區中主河道水體從上游向下游的污染程度逐漸上升.位于主河道上游的郭溪和瞿溪監測斷面距主城區距離較遠,受城市污水排放影響小,水質情況良好.隨著大量污水的排入和高污染的支流水體匯入,主河道水體水質呈現逐漸惡化的趨勢(除仙門斷面),CWQI在南白象斷面達到最高.說明主河道污染程度隨流向具有累加作用.仙門斷面位于城鄉交錯區,與下游城市斷面相比,附近工業企業多,存在畜禽養殖污染,下水管網設施不健全,部分工業廢水和大部分畜禽養殖、服務業和居民生活污水直接匯入排水溝渠甚至直接排入河道.并且,由于附近某些企業、村民違法填埋河道,私建違章建筑,導致該監測斷面附近河床抬高,河道堵塞情況較為嚴重,不利于污染物的擴散.因而仙門斷面的污染程度高于位于主河道下游的西岙和新橋斷面.

從不確定性角度提出的Monte Carlo-CWQI耦合模型具有以下優點:能夠將離散存在的水質評價結果拓展為連續狀態,給出了水質評價參數不確定條件下的所有可能性,有效降低了水質評價中的隨機性和不確定性,為推斷決策提供全面的信息;采用Monte Carlo模擬得到的CWQI是基于河流水質狀態的實際變化,考慮了其取值的可信度,這相對于按一次或多次取樣的均值來確定CWQI的傳統評價方法更為科學、合理,并且能夠減少資料信息的不完整性帶來的統計問題;根據模型模擬結果給出的累積頻率分布圖能夠直觀地顯示水質污染程度的變化.

2.4 靈敏度分析

為探究各水質指標對水體污染的影響程度,計算了模型各輸入參數的SRCC(圖5).各監測斷面TN,NH3-N和DO對CWQI影響很大,SRCC值范圍分別是0.41~0.76,0.25~0.63和0.14~0.66;之后為TP, BOD5和CODMn,其SRCC值處于0.10~0.34,0.09~ 0.30和0.04~0.15;F和Petrol的SRCC值較小,范圍分別為0.02~0.12和0~0.14.需要注意的是,溫瑞塘河水體中NH3-N占TN含量的80%以上,TN的SRCC大部分是由NH3-N貢獻的.故而參數靈敏度分析結果表明NH3-N污染是影響溫瑞塘河流域水質達標的主要原因,河網中NH3-N濃度過高和NH3-N等好氧有機物降解造成的低氧、缺氧問題是該流域面臨的主要水環境問題.控制溫瑞塘河流域內的NH3-N污染是改善該流域水環境質量的關鍵.

由以上分析,建議相關管理部門建立健全污水收集管網建設,截斷直排河道的大部分城市生活污水,對其進行集中處置,這是減輕溫瑞塘河水污染的必要前提和根本方法;推廣人工濕地、沉水植物、生物浮床和植被緩沖區等生態修復技術,通過植物吸收固定水中的氮磷營養鹽,增加河流生態系統的生物多樣性;對低氧、缺氧河段,可以利用曝氣等復氧技術,提高水體中DO的含量,有助于水生態系統從厭氧狀態恢復到好氧環境,改善水體的自凈能力.此外引水沖污,即將水質較好的甌江和珊溪水庫中的水引入溫瑞塘河水系,能夠在短時間內有效緩解水系污染,改善區域環境,推薦在降水量少、水體流動性差的枯水期進行應用.

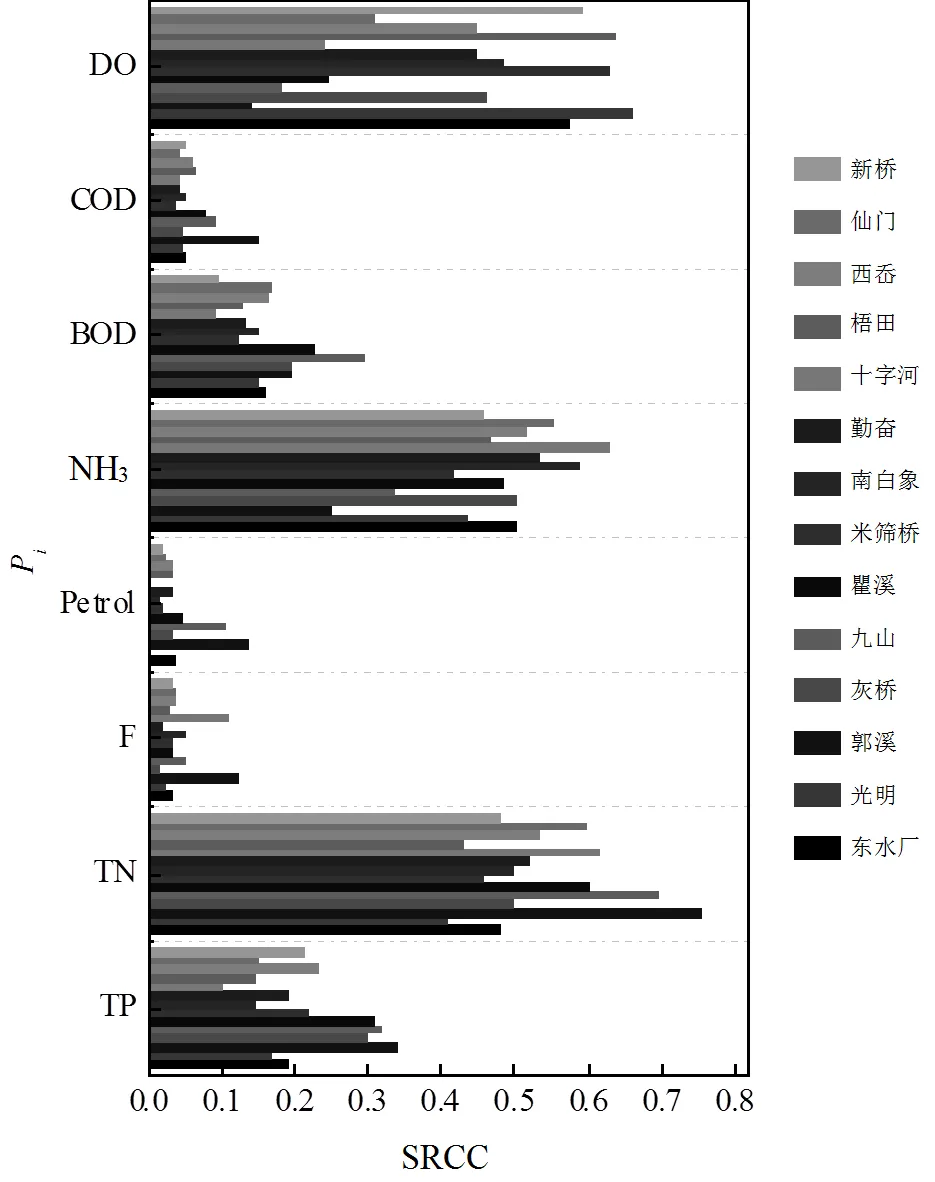
圖5 各監測斷面模型輸入參數靈敏度分析

3 結論

3.1 Monte Carlo-CWQI耦合水質評價模型能夠求出任意可信度下的CWQI,為水環境管理提供更為豐富的決策信息.通過對模型輸入參數的靈敏度分析,能夠表征不同水質指標對水體污染程度的大小,為流域水質改善和水環境管理提供了科學依據.

3.2 溫瑞塘河流域水體污染嚴重,勤奮、九山、東水廠、十字河、南白象、灰橋、新橋、米篩橋、仙門、光明、郭溪、瞿溪、西岙和梧田監測斷面處于重度污染的概率分別為28.50%, 0.55%, 92.71%, 59.73%, 78.85%, 39.38%, 78.87%, 83.09%, 65.32%, 78.08%, 0.00%, 0.96%, 68.09%, 86.06%;處于嚴重污染的概率分別為71.28%, 0.01%, 4.33%, 39.76%, 21.07%, 60.59%, 4.42%, 12.41%, 11.02%, 21.24%, 0.00%, 0.02%, 1.42%, 13.12%.鑒于溫瑞塘河水污染的嚴峻現狀,采取相應的水污染防治措施,以維護河流生態健康刻不容緩.

3.3 TN,NH3-N和DO單因子污染指數的SRCC值是其他水質指標的兩倍以上,表明TN,NH3-N和DO是影響該地區水質達標的主要因子,對水質污染程度有決定性的影響.

[1] Xia X H, Zhou J S, Yang Z F. Nitrogen contamination in the Yellow River basin of China [J]. Journal of Environmental Quality, 2002, 31(3):917-925.

[2] Chang H J. Spatial analysis of water quality trends in the Han River basin, South Korea [J]. Water Research, 2008,42(13):3285-3304.

[3] 于興修,楊桂山.典型流域土地利用/覆被變化及對水質的影響-以太湖上游浙江西苕溪流域為例 [J]. 長江流域資源與環境, 2003, 12(3):211-217. Yu X X, Yang G S. Land use/cover change of catchment and its water quality effects-A case study of Xitiaoxi Catchment in Zhejiang province [J]. Resources and Environment in the Yangtze Basin, 2003, 12(3):211-217.

[4] 林日彭,倪兆奎,郭舒琨,等.近25年洞庭湖水質演變趨勢及下降風險[J]. 中國環境科學, 2018,38(12):4636-4643. Lin R P, Ni Z K, Guo S K, et al. The trend and downside risk of water quality evolution in Dongting Lake in recent 25years [J]. China Environmental Science, 2018,38(12):4636-4643.

[5] 劉 琰,鄭丙輝,付 青,等.水污染指數法在河流水質評價中的應用研究 [J]. 中國環境監測, 2013,29(3):49-55. Liu Y, Zheng B H, Fu Q, et al. Application of water pollution index in water quality assessment of rivers [J]. Environmental Monitoring in China, 2013,29(3):49-55.

[6] 薛巧英.水環境質量評價方法的比較分析 [J]. 環境保護科學, 2004, (4):64-67. Xue Q Y. Comparison and analysis of the methods on water environment quality assessment [J]. Environmental Protection Science, 2004,(4):64-67.

[7] 富天乙,鄒志紅,王曉靜.基于多元統計和水質標識指數的遼陽太子河水質評價研究 [J]. 環境科學學報, 2014,34(2):473-480. Fu T Y, Zou Z H, Wang X J. Water quality assessment for Taizi River watershed in Liaoyang section based on multivariate statistical analysis and water quality identification index [J]. Acta Scientiae Circumstantiae, 2014,34(2):473-480.

[8] Wu Z S, Wang X L, Chen Y W, et al. Assessing river water quality using water quality index in Lake Taihu Basin, China [J]. Science of the Total Environment, 2018,612:914-922.

[9] 徐祖信.我國河流綜合水質標識指數評價方法研究 [J]. 同濟大學學報(自然科學版), 2005,33(4):482-488. Xu Z X. Comprehensive water quality identification index for environmental quality assessment of surface water [J]. Journal of Tongji University (Natural Science), 2005,33(4):482-488.

[10] 萬金保,李媛媛.模糊綜合評價法在鄱陽湖水質評價中的應用 [J]. 上海環境科學, 2007,26(5):215-218. Wan J B, Li Y Y. An application of fuzzy comprehensive evaluation to assessing the water quality of Poyang Lake [J]. Shanghai Environmental Sciences, 2007,26(5):215-218.

[11] 鄒志紅,王學良.基于隨機樣本的BP模型在水質評價中的應用 [J]. 環境工程, 2007,25(1):69-71. Zou Z H, Wang X L. Application of BP modeling based-on random samples to assessment on natural water quality [J]. Environmental Engineering, 2007,25(1):69-71.

[12] 解 瑩,李敘勇,王慧亮,等.灤河流域上游地區主要河流水污染特征及評價 [J]. 環境科學學報, 2012,32(3):645-653. Xie Y, Li X Y, Wang H L, et al., Stream pollution analysis and hydrochemical assessment of the upper Luanhe River Basin [J]. Acta Scientiae Circumstantiae, 2012,32(3):645-653.

[13] 高學平,孫博聞,訾天亮,等.基于時域權重矩陣的模糊綜合水質評價法及其應用 [J]. 環境工程學報, 2017,11(2):970-976. Gao X P, Sun B W, Zi T L, et al. Application of improved fuzzy comprehensive water quality assessment based on weight matrix of temporal distribution [J]. Chinese Journal of Environmental Engineering, 2012,32(3):645-653.

[14] 張欣莉,丁 晶,李祚泳,等.投影尋蹤新算法在水質評價模型中的應用[J]. 中國環境科學, 2000,20(2):187-189. Zhang X L, Ding J, Li Z Y, et al. Application of new projection persuit algorithm in assessing water quality [J]. China Environmental Science, 2000,20(2):187-189.

[15] 李祚泳,張正健.基于回歸支持向量機的指標規范值的水質評價模型[J]. 中國環境科學, 2013,33(8):1502-1508. Li Z Y, Zhang Z J. Model of water quality evaluation with normalized indexes values based on regression support vector machines [J]. China Environmental Science, 2013,33(8):1502-1508.

[16] 王書轉,趙先貴,肖 玲.秦嶺北麓區域主要河流水質分析與評價 [J]. 干旱區資源與環境, 2007,(8):42-47. Wang S Z, Zhao X G, Xiao L. The analysis and appraisal of Mai Rivers’ water quality on the north slope of Qinling Mountains [J]. Journal of Arid Land Resources and Environment, 2007,(8):42-47.

[17] 孫 濤,張妙仙,李苗苗,等.基于對應分析法和綜合污染指數法的水質評價 [J]. 環境科學與技術, 2014,37(4):185-190. Sun T, Zhang M X, Li M M, et al. River water quality evaluation based on correspondence analysis and comprehensive pollution index method [J]. Environmental Science & Technology, 2014,37(4): 185-190.

[18] 陳丁江,呂 軍,金培堅,等.非點源污染河流水環境容量的不確定性分析 [J]. 環境科學, 2010,31(5):1215-1219. Chen D J, Lu J, Jin P J, et al. Uncertainty analysis of water environmental capacity in the non-point source polluted river [J]. Environmental Science, 2010,31(5):1215-1219.

[19] 張應華,劉志全,李廣賀,等.基于不確定性分析的健康環境風險評價 [J]. 環境科學, 2007,28(7):1409-1415. Zhang Y H, Liu Z Q, Li G H, et al. Uncertainty analysis of health risk assessment caused by benzene contamination in a contaminated site [J]. Environmental Science, 2007,28(7):1409-1415.

[20] Qu C S, Sun K, Wang S R, et al. Monte Carlo simulation-based health risk assessment of heavy metal soil pollution: a case study in the Qixia mining area, China [J]. Human and Ecological Risk Assessment, 2012, 18(4):733-750.

[21] 孫清展,臧淑英,張囡囡,等.基于蒙特卡羅方法的扎龍濕地水環境質量評價 [J]. 濕地科學, 2013,11(1):75-81. Sun Q Z, Zang S Y, Zhang N N, et al. Evaluation of Water Environment Quality of Zhalong Wetlands based on Monte Carlo Method [J]. Wetland Science, 2013,11(1):75-81.

[22] Signorino C S. Structure and uncertainty in discrete choice models [J]. Political Analysis, 2003,11(4):316-344.

[23] 楊 陽,代 丹,蔡怡敏,等.基于Monte Carlo模擬的土壤重金屬綜合風險評價與案例分析 [J]. 環境科學, 2015,36(11):4225-4231. Yang Y, Dai D, Cai Y M, et al. Comprehensive risk assessment of soil heavy metals based on Monte Carlo simulation and case study [J]. Environmental Science, 2015,36(11):4225-4231.

[24] 佟瑞鵬,楊校毅.基于蒙特卡羅模擬的土壤環境健康風險評價:以PAHs為例 [J]. 環境科學, 2017,38(6):2522-2529. Tong R P, Yang X Y. Environmental health risk assessment of contaminated soil based on Monte Carlo method: A case of PAHs [J]. Environmental Science, 2017,38(6):2522-2529.

[25] 國家環境保護總局.水和廢水監測分析方法 [M]. 4版.北京:中國環境科學出版社, 2002. State Environment Protection Bureau of China. Water and wastewater monitoring and analysis method [M]. (4th Edition) Beijing: China Environmental Science Press, 2002.

[26] GB3838-2002 地表水環境質量標準 [S]. GB3838-2002 Environmental quality standards for surface water [S].

[27] Ji X L, Dahlgren R A, Zhang M H. Comparison of seven water quality assessment methods for the characterization and management of highly impaired river systems [J]. Environmental Monitoring and Assessment, 2016,188(1):15.

[28] 王肖肖,張妙仙,徐兵兵.模糊標識指數與對應分析法在水質評價中的聯合應用 [J]. 環境科學學報, 2012,32(5):1227-1235. Wang X X, Zhang M X, Xu B B. Combination and application of fuzzy identification index and correspondence analysis method in water quality evaluation [J]. Acta Scientiae Circumstantiae, 2012,32(5): 1227-1235.

[29] 金樹權.水庫水源地水質模擬預測與不確定性分析 [D]. 杭州:浙江大學, 2008. Jin S Q. Modeling and prediction of water quality in headwater area of reservoir and uncertainty analysis [D]. Hangzhou: Zhejiang University, 2008.

[30] 沈曄娜,呂 軍,陳軍華,等.水源區河流非點源污染物入河量計算的水質方程反演方法 [J]. 環境科學, 2010,31(8):1768-1774. Shen Y N, Lu J, Chen J H, et al. Inversion formula of one-dimensional water quality equation for the export loads of nonpoint sources pollution in headwater area [J]. Environmental Science, 2010,31(8): 1768-1774.

[31] 廖 杰,王文圣,丁 晶.貝葉斯公式在河流水質綜合評價中的應用 [J]. 四川師范大學學報(自然版), 2007,30(4):519-522. Liao J, Wang W S, Ding J. Comprehensive assessment of water quality on main rivers in Sichuan by Bayes method [J]. Journal of Sichuan Normal University (Natural Science), 2007,30(4):519-522.

致謝：溫瑞塘河水質監測數據由溫州市環保局提供,在此表示感謝.

River water quality assessment based on Monte Carlo simulation: A case study of Wen-Rui Tang River.

HUANG Hong1,2,3, SHANG Xu1,2,3, MEI Kun1,2,3, WANG Zhen-feng1,2,3, XIA Fang1,2,3, HUANG Shu-hui1, ZHANG Ming-hua1,2,3, JI Xiao-liang1,2,3*

(1.School of Public Health and Management, Wenzhou Medical University, Wenzhou 325035, China；2.Key Laboratory of Watershed Science and Health of Zhejiang Province, Wenzhou 325035, China；3.Southern Zhejiang Water Research Institute (iWATER), Wenzhou 325035, China)., 2019,39(5)：2210~2218

Accurate evaluation of the pollution magnitude in a water body is an important premise for effective water pollution prevention and control. This study used Monte Carlo simulation method together with comprehensive water quality index (CWQI) method and statistical analysis of measured water quality parameters to assess water quality. The Wen-Rui Tang River watershed was used as the study site. Through the combined model and water quality data from 14 monitoring sites at Wen-Rui Tang River during 2004 to 2010, the probability of each site for every pollution level and the influence of each water quality parameter on water pollution were quantified. The results of Monte Carlo-CWQI coupled model indicated that the water quality of Wen-Rui Tang River was highly impaired. The probabilities of the water impairments at sites of Qinfen, Jiushan, Dongshuichang, Shizihe, Nanbaixiang, Huiqiao, Xinqiao, Mishaiqiao, Xianmen, Guangming, Guoxi, Quxi, Xi-ao, and Wutian being at the heavy pollution level were 28.50%, 0.55%, 92.71%, 59.73%, 78.85%, 39.38%, 78.87%, 83.09%, 65.32%, 78.08%, 0.00%, 0.96%, 68.09%, and 86.06%, respectively. The probabilities of the water impairments at these monitoring sites being worse than heavy pollution level were 71.28%, 0.01%, 4.33%, 39.76%, 21.07%, 60.59%, 4.42%, 12.41%, 11.02%, 21.24%, 0.00%, 0.02%, 1.42%, and 13.12%, respectively. The spearman rank correlation coefficient for total nitrogen (TN), ammonium-nitrogen (NH3-N) and dissolved oxygen (DO) respectively ranged from 0.41 to 0.76, 0.25 to 0.63 and 0.14 to 0.66, which were more than twice on the values for other parameters. This result implied that TN, NH3-N and DO were the dominant factors affecting the rate of reaching water quality standard in Wen-Rui Tang River. This investigation can broaden the viewpoints for researches and managers on river water quality evaluation and can provide abundant information for decision-making on water environment management.

Monte Carlo simulation；water quality assessment；uncertainty；Wen-Rui Tang River

X522

A

1000-6923(2019)05-2210-09

黃 宏(1982-),男,廣西靖西人,博士,助理研究員,碩士生導師,主要從事流域非點源污染防控及環境與人群健康風險方面的研究.發表論文20余篇.

2018-10-26

國家自然科學基金資助項目(41601554,41807495);溫州市基礎性科研項目(S20180005)

*責任作者, 助理研究員, jixiao556677@126.com