一類新的基于元胞自動機的S盒的密碼學性質研究

關杰，黃俊君

（解放軍戰略支援部隊信息工程大學密碼工程學院，河南 鄭州 450001）

1 引言

基于元胞自動機（CA, cellular automaton）的S盒[1]因其良好的密碼學性質及較低的實現成本被廣泛應用到許多密碼算法中，其中最典型的是已經作為SHA-3標準[2]之一的Keccak雜湊函數[3]。本文選用了一個作用域范圍僅為3個元胞的局部規則，從而使該算法的S盒有著極小的軟件實現成本及硬件實現消耗。目前，接觸到的其他利用元胞自動機的局部規則定義S盒的密碼都使用了與Keccak雜湊函數的 S盒相同的局部規則，如 Panama[4]、Subterranean[5]和 3Way[6]。除了這些 S盒外，還有一些密碼算法使用的S盒是Keccak雜湊算法的S盒的仿射變換，如Ascon[7]。

本文通過實驗找到了一類新的基于元胞自動機的S盒，并對這一類S盒的密碼學性質進行研究，該類S盒相比Keccak雜湊函數的S盒差分性質更好，并且在輸入輸出規模為5時也是一個置換，因此這一類新的S盒有潛力代替Keccak雜湊函數的S盒，為密碼設計者提供設計參考。

2 基本概念

2.1 S盒的密碼學性質

在分組密碼的設計中，最通用的設計準則就是香農提出的混亂和擴散原則[8]。在實際的設計過程中通常使用S盒來提供混亂效果，在很多密碼中S盒都是唯一的非線性環節。一個m進n出的S盒可以用映射表示，其中，m、n都是正整數。

置換性質[9]和差分性質是S盒重要的密碼學性質，具有良好差分性質及滿足置換條件的S盒將有更廣泛的應用場景。下面給出置換和差分的定義。

定義1[10]設，若對任意且，有，稱F是一個置換。

定義2[11]設，那么稱為F在輸入差分為α，輸出差分為β下的差分轉移概率，其中，#{?}代表集合中元素的個數。

2.2 元胞自動機

元胞自動機是一種廣泛應用在不同領域，用來模擬和分析復雜離散問題的并行運算模型。一個CA可以表示為一個由元胞（cell）組成的元胞空間（lattice）。在每一步狀態更新中，元胞空間中的每一個元胞根據局部規則（local rule）同步更新狀態。CA中所有元胞的狀態從原有狀態到一步更新后的狀態之間的映射可以用全局規則（global rule）來表示。事實上，如果經過合理的設計及選取，全局規則可以是一個具有良好密碼學性質的非線性映射，即本文要研究的基于CA的S盒。根據劃分的不同，CA有很多分類，本文僅考慮一種可以用作S盒的一維布爾型循環邊界CA，這種CA的定義如下。

可以把元胞空間看作是等間隔排列在直線上的一系列完全相同的元胞，且每個元胞的狀態均取自集合Z2={0,1}。

設Z*為整數集合，假設元胞空間的規模為n且n∈Z*，即該CA由n個元胞組成，那么所有元胞的狀態可以用一行有限的符號序列來表示，當其中每一個符號取特定狀態就可以構成一個狀態序列，稱每個這樣的狀態序列為CA的一個構型。構型中的每一個元胞是用取自Z2的狀態來表示的，例如構型X可以表示為，其中，

在一次狀態更新中，設更新前的構型為X，那么更新后的構型完全由X決定，記為X′。其中，X′中第i個元胞x′i的狀態由X的xi及其右邊不超過r(r≤n-1)個元胞的狀態決定，即

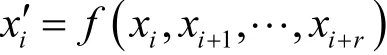
下面，給出一維布爾型循環邊界CA的定義，如定義3所示。

定義 3[12]映射為一維布爾型循環邊界 CA，其中，*n∈Z為元胞空間的規模，存在r＞0及，對 CA的任意構型，有

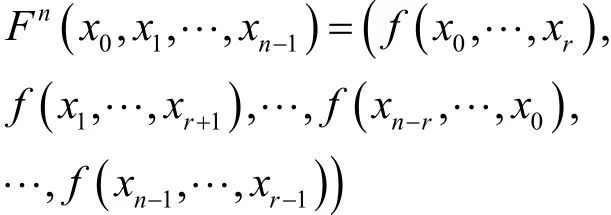
其中，r為CA的鄰域半徑，f為CA的局部規則，Fn為CA的全局規則。

圖1是一維布爾型循環邊界CA的示例，其元胞空間的規模n=5，局部規則可表示為，且其鄰域半徑r=2。可以看到，在這種循環邊界的CA中，其元胞空間可以看作一個首尾相接的環，最開始的元胞接在最后一個元胞后，因此在更新最后r個元胞的狀態時，會從最開始的r個元胞中選取部分作為其右鄰域的一部分。在圖1中，CA向量的最右側用最開始的r=2個元胞接上，在最后2個元胞更新時可以作為其右鄰域。

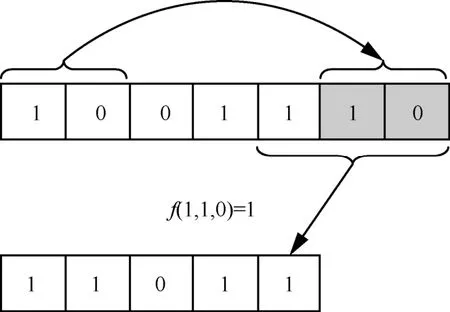
圖1 一維布爾型循環邊界CA示例

圖1中的CA的局部規則就是用于Keccak的非線性變換χ，本文將該CA的局部規則記為fK，全局規則記為。

接下來，本文將給出CA的一個重要性質。本文所有運算都是在模n上進行的。

定理1CA的平移不變性。設為一個 CA，其局部規則為，其中n∈Z*,r＞0且n＞r，設為該CA的構型，令σk(X)為對X循環左移k位，那么?X、?k∈Zn均有

證明令，那么，所以有

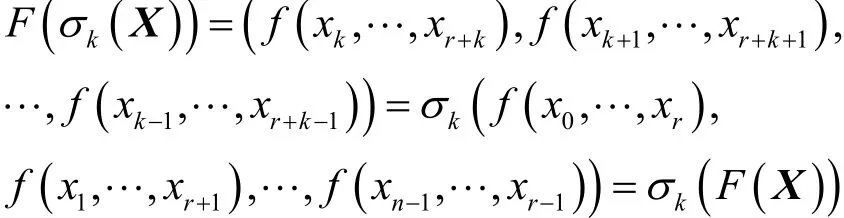
故結論成立，證畢。

在一般的CA中，局部規則對第i個元胞xi的作用域為，不僅跟右鄰域相關，還與左鄰域相關。但是根據定理1可知，把CA的構型經過平移后可以與上文介紹的CA的局部規則一樣，僅與右鄰域相關而不改變其置換性質和差分性質。

2.3 一類新的基于CA的S盒

由于用全局規則就可以唯一地表示一個 CA，而一個CA經過合理地設計后，可以使全局規則成為一個密碼學性質良好的非線性變換，從而可以用作密碼環節中的S盒。為了找到密碼學性質良好的基于CA的S盒，本文通過實驗窮舉了規模為5的所有CA并從中篩選出一個CA。該CA具有良好的差分性質且滿足置換條件，然后本文將其在不同的規模下的情況抽象成一類CA。

下面，給出本文要研究的這一類新的基于 CA的S盒的定義。

定義 4設n≥5，映射為一類CA，其局部規則為且滿足

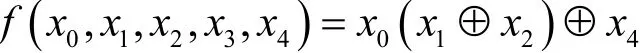
3 的置換性質分析

置換性質是S盒一個重要的密碼學性質，滿足置換性質的S盒在很多密碼體制中實現數據變換，具有廣泛的應用場景。

引理1對于元胞空間規模n為偶數的CA，設局部規則為f(x0,x1,…,xr)且r＜n，若r為奇數，有若r為偶數，有那么該 CA的全局規則n

F必然不是一個置換。

證明設X、X*∈Z2n，如果能夠找到X≠X*，使得F(X)=F(X*)，那么F不是一個置換。由于n為偶數，本文令令X*=若r為奇數，有

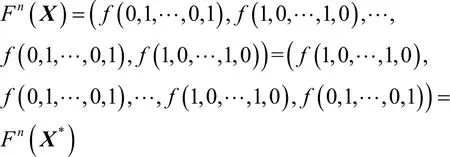
若r為偶數，有

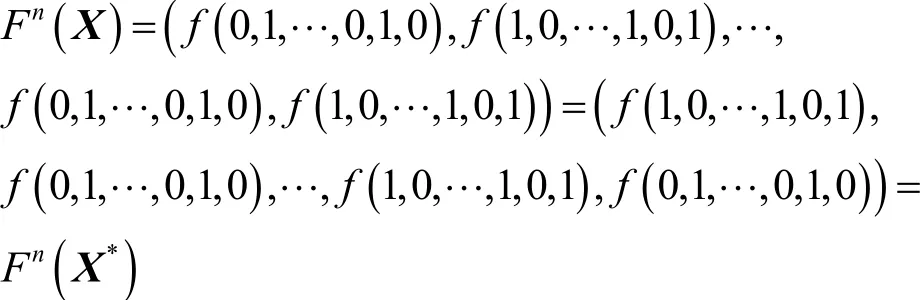
顯然，此處X≠X*，但有所以此時全局規則nF不是一個置換，證畢。事實上，Keccak中的非線性映射的全局規則在n為偶數時不是一個置換，因為對應的局部規則fK有，根據引理1即得。

引理 2設n≥6且n為奇數，對于，有對于

證明首先，令，令X′=那么有

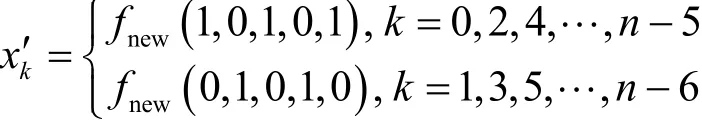
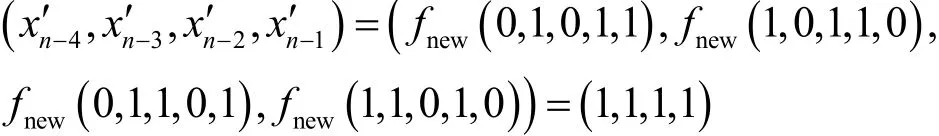
當n=7時，令X=(1,1,1,1,0,0,1)，容易驗證成立；當n=9時，令X=(1,1,1,1,0,0,1,0,0)，同樣有0,1,1,1,1)成立；當n≥11時，令X=(1,1,1,1,0,0,1,，驗證有。又因為

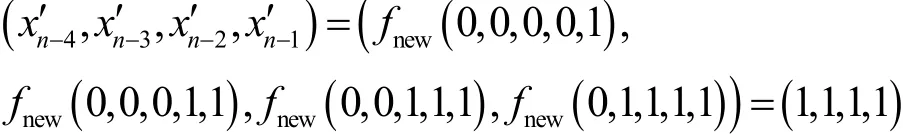
綜上所述，結論成立，證畢。

定理2 設，當n=5時，是置換；當n≥6時，不是置換。

證明對于，容易驗證遍歷 32個輸入X會有對應 32個不同的輸出Y，即對于任意的，必然有Y≠Y*，所以是置換。

下面，分2種情況討論n≥6時不是一個置換。

情況1n≥6且n為偶數，此時由得

所以根據引理1可知，當n為偶數時不是一個置換。

情況2n≥6且n為奇數，由引理2可以構造同時可以構造，也有但是，所以此時也不是一個置換。

綜上所述可知，當n≥6時，均不是一個置換，證畢。

4 的差分性質分析

令n∈Z*，設，記的輸入差分為，輸出差分為，由于，那么輸入差分和輸出差分之間滿足如式(1)所示的等式。

本文把n位輸入差分和輸出差分的關系用n個式子組成的方程組來表示，如式(2)所示。

該差分方程組對應的n維系數矩陣就是的差分矩陣，記為A，如式(3)所示。

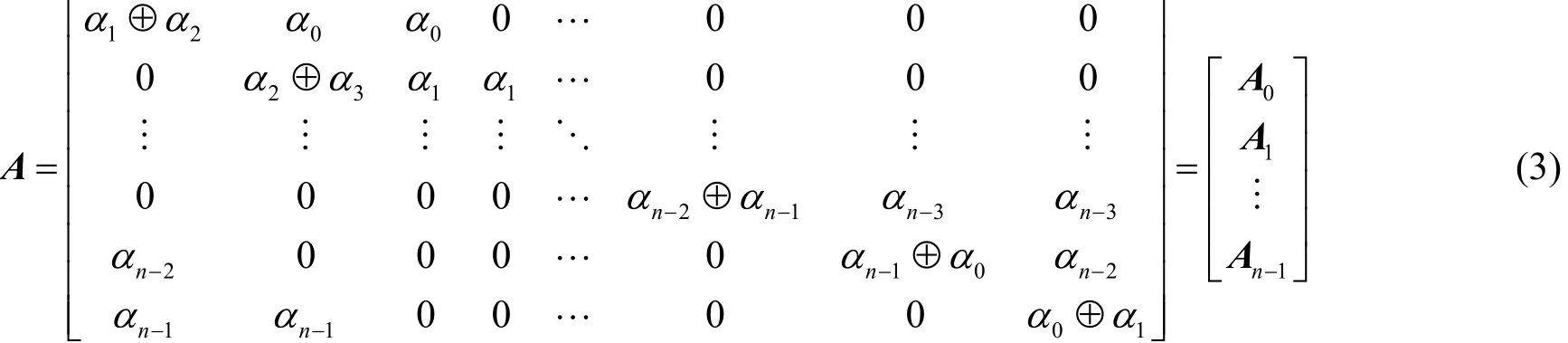
其中，Ai(i∈{0,1,2,…,n-1})表示A的第i行。另外，A僅與的輸入差分相關。

定理 3設n≥5，對于，任意輸入差分及輸出差分β，若差分轉移概率，那么一定有其中表示A的秩。

證明設的輸入，輸入差分及輸出差分分別為和。其中，。由式(1)可得

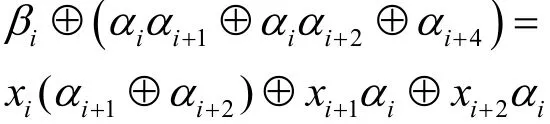
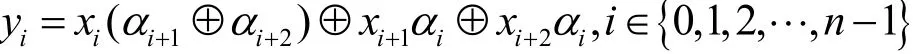
對于確定的iα及iβ，本文可以得到方程組系數的值及yi的值，所以該方程組就是Z2上的非齊次線性方程組，并且其系數矩陣即為的差分轉移矩陣A。將該非齊次線性方程組用矩陣形式表示，如式(4)所示。

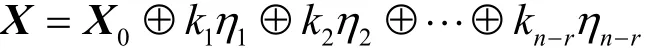
其中，ki∈{0,1}，ηi是方程組線性無關的基礎解系，。遍歷所有的ki可以得到所有方程組的解，所以解的個數為2n-r個，也就是說所以有

證畢。

定理4設n≥5，對于，任意輸入差分α及輸出差分β，若差分轉移概率不為0和1，那么

證明設的輸入輸入 差分，輸出差分β=

首先，對任意選定的α≠0及輸出差分β，若存在X滿足，則顯然X⊕α滿足此式，所以非零時必為偶數。故當差分轉移概率非零時，其最小值為，所以顯然成立。

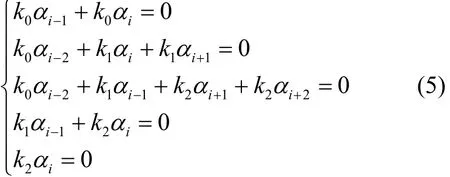
由k2αi=0可知k2=0。下面分別討論αi-1取值為0和1這2種情況。

情形 1若αi-1=0，由得k0=0。因為k0、k1、k2不全為0，所以必有k1=1。那么由得αi+1=αi= 1，最后根據有αi-1=0。考慮，經初等變換后有

情形2若αi-1=1，由知。因為不全為0，所以必有k0=1。

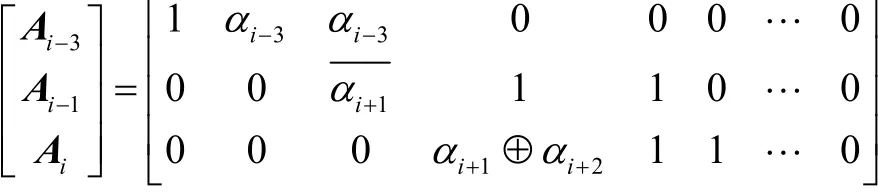
經過上面討論可知，對任意輸入差分α≠0，A的秩r≥3。根據定理3，任取輸出差分β，若β)≠0，則必有證畢。

5 的差分分布

定理 5設n≥5，對于，任意輸入差分及輸出差分，設σk(α)為對α循環左移k位，那么令若且，則

證明不妨先設k=1，對有。記在輸入差分為α與α′時的差分轉移矩陣分別為和那么有

在Z2上對其進行初等變換可以轉化為

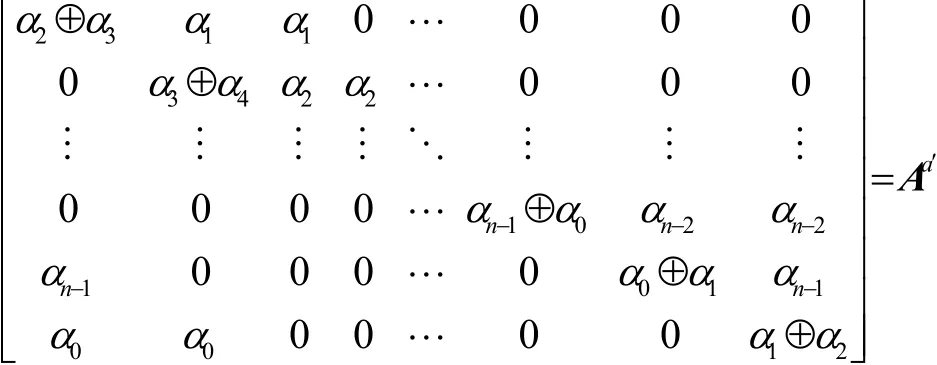
另外只需將上面的α替換成σ1(α)，α′替換成σ2(α)，就有k=2時成立。同樣地，k為其他值時定理均成立，證畢。

定理 6設n≥5，對于，給定輸入差分設α的漢明重量為w(α)，對于任意輸出差分β，若，那么當或

證明當w(α)=1時，考慮α′=(0,0,…,0,1)時的情況，即而其余位置均為 0。此時將在Z2上進行初等變換，可以得到有3行非零的階梯型矩陣所以此時A的秩r=3，由定理3可知，對于任意輸出差分β，若。又由定理5，若w(α)=1，必然存在使得，所以時就有

當w(α)=n-1時，同樣地，考慮時的情況，即α0′=0而其余位置均為1。此時，在2

Z上進行初等變換，可以得到有n-1行非零的階梯型矩陣所以A的秩r=n-1。由定理3可知，存在2n-1個不同的β使。又由定理5，若必然存在使所以時就有

根據定理5可知，循環移位等價的2個輸入差分對應的非平凡差分轉移概率是相等的。從而本文可以根據循環移位等價將w(α)=2和w(α)=3時的α進行分類。

的輸入差分α在w(α)=2時根據循環移位等價可以分為{σk(5)|k∈Z}={5,9,10,18,20}和2類。在w(α)=3時也可以分為和兩類。由定理5可知，同一類中的輸入差分對應相同的非平凡差分轉移概率。經驗證可知，{σk(5)|k∈Z}和{σk(11)|k∈Z}對應的非平凡差分轉移概率記這2個集合的并集為；而{σk(3)|k∈Z}和{σk(7)|k∈Z}對應的非平凡差分轉移概率，記這2個集合的并集為至此本文已經得到的輸入差分α在w(α)=2和w(α)=3時對應的非平凡差分轉移概率情況。

定理 7設的輸入差分為α，其漢明重量為w(α)，對任意β∈Z5，如果當且僅當時，；當且僅當時

證明由于w(α)∈{0,1,2,3,4,5}。當w(α)=0時，或1；由定理6，當w(α)=4或w(α)=5時，若，則有，則有又根據上面的討論，當w(α)=2或w(α)=3時，若α∈Ω1，，而當w(α)=1時，若則其對應的非平凡差分轉移概率，而若α∈Ω，則其對應的非平2凡差分轉移概率

表1 和的差分轉移概率計數

表1 和的差分轉移概率計數

差分轉移概率 5 F 5 n e w F K 1 1 1 1 4 0 2 0 1 8 1 2 0 1 2 0 1 6 2 5 6 1 7 6 0 6 4 7 7 0 7 1

6 結束語

雖然目前有許多密碼已經使用了基于元胞自動機的S盒，但都使用了Keccak的局部規則或者仿射變換。本文通過實驗找到了一類新的基于元胞自動機的S盒并研究了其置換性質和差分性質，證明了該類S盒在規模為5時是一個置換，并且其非平凡差分轉移概率的取值范圍為而Keccack的S盒的非平凡差分轉移概率的取值范圍則為另外，本文進一步研究了該類S盒在規模為5時的差分分布情況，給出了該類S盒在取到最大和最小非平凡差分轉移概率時的充要條件。最后通過比較和的差分轉移概率的計數情況可以發現，相比差分分布更加均勻。所以該類S盒有著比Keccak類S盒更好的差分性質。接下來的工作重點是從理論上研究這類 S盒抵抗線性分析以及立方攻擊[14]等各類攻擊方法的效果。