分數階Fourier變：在水聲信號處理中的應用研究

冷龍龍 肖業偉 胡軍

摘要：線性調頻（IFM）信號瞬時頻率隨時間呈線性變化，當干擾噪聲與其強耦合時，經典的濾波方法難以有效的濾除噪聲。針對水聲通信中采用LFM信號作為載體時濾波效果不明顯的問題，提出了一種改進的分數階Folmer變換（FRFT）濾波方法。水聽器接收到的LFM信號在最佳變換域經FRFT變換后，同時對期望信號進行FRFT變換，系數修正后再對信號進行窄帶濾波處理。仿真結果表明，在信噪比高于-12dB時，新算法能夠有效的實現信噪分離，還原出信號。

關鍵詞：線性調頻信號;水聲通信;分數階Follrier變換;窄帶濾波

中圖分類號：TB566

文獻標識碼：A

水聲信道因其特殊的時空頻變特性，水聲通信的發展遠遠滯后。對水聲通信技術的研究已成為各國科學家和工程技術人員研究的熱點。水聲信號提取優劣將會直接影響水下目標探測、定位、跟蹤等技術的發展。線性調頻（LFM）信號瞬時頻率隨時間呈線性變化，將其作為載波信號應用于水聲通信中，能夠提高系統的抗噪聲干擾、抗多徑干擾和頻率選擇性衰減的能力[1]。分數階Fourier變換是近年來數字信號處理領域一種很重要的算法，一個LFM信號在某一特定階次的分數階傅里葉變換域上是一個函數。因而將分數階Fourier變換引入到水聲信號處理方面，對于發展基于分數階Fourier變換的水聲通信技術具有積極的意義。

文獻[2]提出了一種基于分段頻率擬合的多階分數階傅里葉變換（FRFT）自適應濾波方法，通過擬合頻率曲線來確定FRFT濾波算法的各個參數。文獻[3]提出了一種簡潔的分數階傅立葉變換（ CFRFT）方法，降低了分數階Fourier變換濾波算法的復雜度。文獻[4]利用分數階傅里葉變換在分析線性調頻信號時的優良特性，在分數階變換域上進行自適應濾波處理，提高信號檢測估計效果。文獻[5]利用調頻步進雷達的粗距離像信號為慢時間域的線性調頻信號的特點，通過對若干個連續子脈沖串的分數階傅里葉變換譜圖進行等距滑動疊加的方法，解決了單個子脈沖串的FRFT譜圖在被噪聲淹沒的問題。但當信噪比較低時，且干擾噪聲與待觀測信號具有較強的時頻耦合，經典的濾波方式難以實現有效的信噪分離。

針對以LFM信號為載體的水聲通信方案，對傳統FRFT濾波算法進行優化。在窄帶濾波前，對已知起始頻率和調頻斜率的載波信號（期望信號）進行FRFT變換，在每個步長點計算其與水聽器收到的LFM信號的差值，該差值即為干擾噪聲在分數階Fourier最佳變換域的值，系數修正后進行窄帶濾波處理，再進行FRFT反變換，即可恢復原信號。

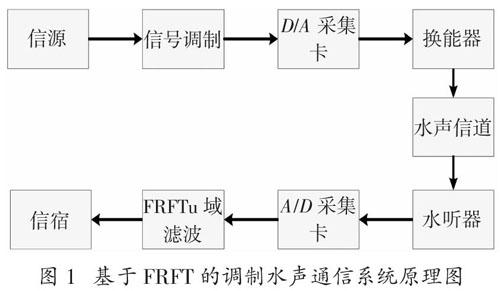
1 基于FRFT的調制水聲通信方案

水聲通信方案如圖1所示，采用LFM信號作為載體，采用分數階Fourier變換濾波方法作為解調機制。信號調制后送人D/A采集卡，利用D/A采集卡將數字信號轉化為模擬信號送人到水聲換能器，水聲換能器將模擬信號轉換為聲信號發送到水聲信道中，水聽器將接收到的模擬信號轉換為A/D采集卡能夠處理的數字信號，利用FRFT濾波算法對轉換后的含有噪聲的LFM信號進行濾波解調處理，供進一步研究分析。

2 分數階Fourier變換

2.1 分數階Fourier變換定義

在t域的函數x（t）的p階分數階傅里葉變換是一個線性積分運算，其定義式為：

3.3 分數階Fourier變換濾波評價指標

濾波算法的效果可用信噪比改善因子IF來衡量，其定義為濾波前后的信噪比之比：

由以上分析可知，信號經FRFT濾波處理后，若信號能量越集中，則所需選取的窄帶通的濾波器的帶寬越窄，殘余噪聲越少，改善因子會越大即濾波效果更好。

3 基于分數階Fourier變換的LFM信號濾波算法

3.1 LFM信號特點

線性調頻信號又稱chirp信號，LFM信號的一般表達式為：

式中f0為信號中心頻率，k為線性調頻信號的調頻斜率，A（t）為瞬時振幅，φ0為初始相位，為了計算方便，一般設置幅值A（t）=0，初始相位φ0=O，故LFM信號可簡化為：

S（t）=expU（2rrf0t+πkt²）]（18）

線性調頻信號由于其非平穩性，在時頻域內，常用的處理平穩信號的濾波算法對其進行濾波效果不佳，而分數階Fourier變換（FRFT）可以解釋為信號在時頻面內繞原點旋轉任意角度后在分數階Fourier域的表示，將信號在時頻平面上旋轉特定的角度，對信號進行旋轉分離來濾除噪聲[7-8]。同時LFM信號的分數階Fourier變換是一個線性變換，分數階傅里葉變換特別適合處理LFM信號[9-10]。

結合式（2）和式（18）可得：

3.2 分數階Fourier變換濾波原理

由傅里葉變換可知，信號可以展開成n組不同頻率正弦波的疊加[11]，信號在時頻域的投影如圖3所示。在時域表現為連續的方波信號，在頻域部分表現為不同頻率的正弦波的無限疊加，投影到頻域平面上表現為不同頻率段。傳統傅里葉變換濾波算法是將時域信號變換到頻域信號，即將時域軸旋轉π/2，然后濾除不需要的頻率分量。而分數階Fourier變換濾波算法進行濾波原理是基于時頻平面旋轉的信號濾波方法，即將信號在時頻平面上旋轉特定的角度（a=p π/2），對信號進行旋轉分離，從而達到抑制噪聲的目的。在分數階Fourier變換域上，多了一個變換階次的自由參量，且同時融合了信號在時間域和頻率域的特征信息，故分數階Fourier變換濾波算法被認為是一種有效的時頻分析方法，適用于處理如Chirp類的非平穩信號。

LFM信號是非平穩信號，在時間域與頻率域上都有較大的時寬和帶寬，若采用常用的處理平穩信號的濾波算法對其進行濾波效果并不理想。LFM信號瞬時頻率隨時間呈線性變化（f+kt），LFM信號投影到時頻面就是一條直線段。該線段與時間軸夾角為β，當FRFT的旋轉角度α與β正交，LFM信號在FRFT域上的投影就聚集在一點上，通過該點的分數階Fourier域上的帶通濾波便能很好的濾除掉噪聲[12-14]。

[7]劉秉瑞，粟嘉，基于FrFT的自適應寬帶干擾抑制算法[J]中國電子科學研究院學報，2016， 11（03）：319-325.

[8]王瑜，李小波，周青松，等，基于FRFT窄帶濾波的LFM信號研究[J].火力與指揮控制，2016，41（12）：41-43+49.

[9]王春陽，劉雪蓮，分數階Fourier變換在信號處理中的應用研究[J].長春理工大學學報.2015，38（5）：1672-1680.

[10] HAN J，WANG Q，QIN K.The non -stationary signal of time -frequency analysis based on fractional Fourier transform andWigner -Hough transform [M]. Mechatronics and AutomaticControl Systems. Springer International Publishing， 2014.

[11]張賢達，現代信號處理[M].北京：清華大學出版社，2002.

[12]趙硯博，寬帶水聲信道參數估計及應用[D].廣州：華南理工大學，2016.

[13]韓博文，楊小鵬，基于FrFT域濾波的靈巧噪聲干擾抑制方法[J].信號處理，2017，33（12）：1602-1608.

[14] ZHAI M Y.Seismic data denoising based on the fractional Fouriertransformation [J].Journal

of Applied

Ceophysics， 2014， 109：62-70.

[15] LIN L F，YU L， WANC H Q，et al.Parameter-adjusted stochasticresonance system for the aperiodic echo chirp signal in optimalFrFT domain [J]. Communications in Nonlinear Science andNumerical Simulation. 2017. 43： 171-181.

[16]朱健東，趙擁軍，唐江，線性調頻連續波信號的周期分數階Fourier變換檢測與估計[J].電子與信息學報，2013，35（8）：1827-1833.