基于距離統計的有序紋理點云離群點檢測

黃旺華 王欽若

摘要：三維數據的離群點檢測是紋理點云數據處理的重要內容之一，為了有效快速地檢測離群點，根據紋理點云的有序結構特征，提出了基于距離統計的檢測算法。首先在每個點到其K鄰域中其他點距離的基礎上計算出K鄰域距離;然后根據有序點云中該距離符合正態分布的特點和正態分布3u定理，將超出3倍方差范圍的點認定為離群點。實驗結果顯示算法采用曼哈頓一最大距離進行檢測，當K為4時可以更加快速準確地將有序點云中的離群點檢測出來。由此得出，基于距離統計的算法可以有效地將離群點檢測出來，同時成功地應用于紋理點云的離群點檢測。

關鍵詞：離群點檢測;距離統計;K鄰域距離;正態分布3cr定理;有序點云

中圖法分類：TP391.72

文獻標識碼：A

自然界中如木紋、皮革和石紋等紋理，具有細微、相似但不完全相同等特征，由于其美輪美奐的形狀，經常應用于工業設計、藝術設計、服飾設計和模具設計等方面[1'2]。紋理的數字化是獲取紋理數據的主要手段之一，可以通過視覺技術進行獲取，數據形式主要有二維平面[3，4]和三維空間[5'6]。三維的紋理數據不但可以具有顏色信息，更主要有空間信息，可以提高紋理的設計和展示效果。

采用線激光掃描技術對紋理物體進行三維數據的掃描是常用的三維紋理數據獲取手段之一，但由于受到各種因素影響，特別是皮革的光滑表面，經常出現一些不可預測的離群數據[7]。在對三維數據進行處理之前需要將這些離群點進行識別和處理，稱為離群點檢測。離群點檢測是數據處理中的熱點研究內容[8-12]，是數據挖掘技術[13，14]中主要的任務之一，主要用于從某一數據集中識別出與整體不相符的小部分異常數據，廣泛應用于各種領域的安全監測，檢測出異常的數據。

離群點檢測技術大概可分為5種[15，16]，分別為基于統計、距離、密度、聚類和深度的離群檢測。基于統計的檢測是指數據符合某個分布模型，比如正態或泊松分布，將處于低分布概率的數據定義為離群點[17]。基于距離的檢測主要判斷點到數據集中大部分或K鄰域的距離是否大于某個閥值這[18，19]。基于密度的檢測是在計算點的局部密度和相對密度的基礎上，判斷該點是否是離群點[20]。Bhattacharyac21]提出類似于密度的相鄰秩次偏差將數據空間劃分為正常數據可異常數據。基于聚類是根據某條件將數據分成幾類。Daneshpazhouh[22]提出基于模糊聚類的半監督離群點檢測方法，該方法應用于存在正常數據并不標簽的情況下，首先通過KNN算法識別出非正常的數據，然后使用模糊聚類將數據劃分為正常數據和非正常數據。在深度離群點檢測中，認定中心點為正常點，然后計算數據每個點到中心點的深度值，值越大說明是處在邊緣的離群點[23]。

在對細紋理進行線激光掃描過程中，采用激光三角法獲取深度信息，而兩水平方向的取值是分別是均勻間隔取值，最終獲取有序的點云數據。由于掃描對象皮革等光滑的表面，獲取的點云數據中存在個別離群點。為了有效利用點云的有序特點，提高數據的處理速度，文中根據相鄰點的距離符合正態分布的現象，采用距離和統計分布結合的離群點檢測方法。

論文主要結構如下：第1節討論了有序點的距離統計離群點檢測的相關理論工作;第2節主要介紹了本文的離群點檢測方法;第3節對文中的檢測方法進行實驗驗證和分析;最后一節是討論和結論。

1 相關理論

1.1 有序點云K鄰域距離

定義1：有序點云P（M，N），表示M行Ⅳ列的網格點云數據集，其中點p（m，n）ED（M，Ⅳ），每個點包含三維空間坐標，p（m，n）：=[x，y，z]。

由正態分布的30-定理可知，數值分布在3倍方差范圍內的概率為99.74%，超出該范圍的數值可以被認定為是異常數據。

2 有序紋理點云的離群點檢測算法

2.1 算法描述

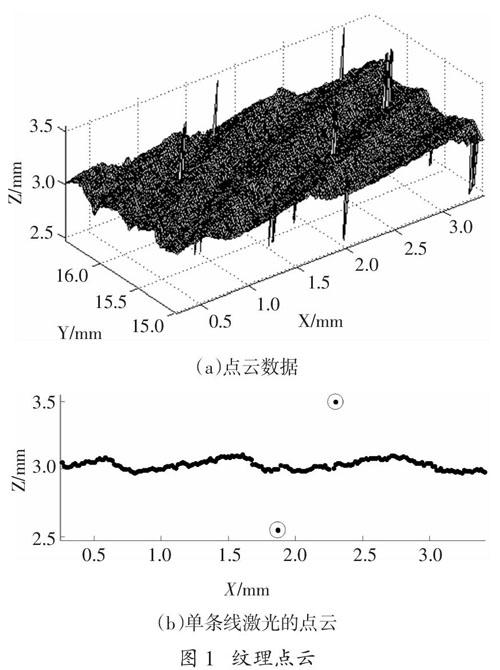
一般情況下，紋理是附著在物體表面比較細微的痕跡，通過激光掃描所獲取的點云數據主要集中在一定的平面內，但在掃描過程中，由于環境和掃描對象光滑表面的影響。如圖1所示為某小部分有序紋理點云數據，存在離群點偏離了正常范圍，如在圖l（a）中尖峰位置對于的點，其中圖l（b）是圖l（a）的其中一條線激光提取的點云，在正常值上方和下方都存在離群點點，如圖l（b）中圓圈標注，其他是正常取值點。

為了將有序點云的離群點快速的檢測出來，文中充分利用點云的有序性和在掃描過程中的規則網格特點。有序點云P（M，N）中的離群點檢測方法如下：

1、計算點p_i（m_i，n_i）的K鄰域中K個點的歐氏距離或曼哈頓距離。

2、計算點p_i的K鄰域距離，求取點p_i的K個距離的平均距離或最大距離。

3、計算點云所有點K鄰域距離的均值和方差，當d（p_i，P，k）>μ+3σ或d（p_i，P，k）<μ- 3σ判定該點為離群點。

2.2 時間復雜度分析

本算法充分利用了線激光掃描獲取的點云數據有序性和X-Y平面網格特點，在計算點的K領域距離時，根據點云體素在X-Y平面位置的相鄰關系，直接獲取點的K領域的所有點，避免了傳統離群點檢測算法中最差復雜度0（n2）的K鄰近點搜索過程。算法主要分成三部分，首先計算每個點到鄰域K個點的距離，在該部分的時間頻度可以記為T（K*n）。第二部分是求取K鄰域距離，不管是平均距離還是最大距離，時間頻度記為T（n）。最后是對每個點進行判斷，時間頻度也記為T（n）。整個算法的時間頻度為T（（K+2）*n），則其時間復雜度為O（n）。

3 實驗結果及分析

為了驗證該有序點云的距離統計離群點算法的檢測有效性、精度和效率，采用實驗室自主研發的高精密三維掃描設備對紋理皮革進行掃描，將獲取的點云數據作為測試數據[24]。算法將在Windows7（64位）+MATLAB的軟件環境中進行驗證，硬件配置為Intel 13 2.4GHz的CPU和8G的內存。在實驗中將本文的算法與LOF[20]和LDOF[19]進行離群點的檢測效果比較和分析，同時對算法中的K值進行分析。

3.1 實驗環境及數據

如圖2（a）是本實驗室專門用于掃描細紋理的高精密三維掃描設備，設備主要包括計算機、運動控制平臺、工業相機和激光器等。當掃描物件大小超出相機的有效視場時，需要多次對其進行多次不同區域的掃描，如圖2（b）是一次性掃描紋理皮革的Z軸數據生成的平面圖像。點云數據在X方向最大的寬度為1536體素，體素間X方向的距離為0.015毫米（如圖1所示），而在Y方向由運動控制平臺和工業相機，每0.015毫米間隔系統提取一條激光線的深度值作為Z方向的取值。在Z方向，根據激光三角法計算光條中心，為方便運行由系統設定正常紋理皮革的取值為3毫米左右，當由于皮革表面光滑及其他外界因素的影響，偏離正常光條線的點取值約為2.5毫米或3.5毫米。如果離群點主要是由表面光滑原因引起，一般情況下，該區域出現離群點團，如圖l（a）右邊區域，上邊和下面均出現有離群點團。

在本實驗中，雖如圖l（b）中樣本數據的有序點云的大小為3338x1536體素，但為了方便展示算法的效果，文中將只展示某一區域的檢測效果進行測試、比較和分析。

3.2 實驗結果及分析

一）與LOF和LDOF檢測效果對比

如圖3是采用本文算法對如圖3（a）帶有離群點的點云數據進行檢測的效果對比圖。圖3（a）是圖2（b）樣本數據中的一小部分，大小為300x150，圖中的下方存在個別的離群點和多個離群點形成的離群點團。圖3（b）是本文算法的離群點檢測效果，算法中采用歐氏距離計算點與點之間的距離，然后在K=8領域中求取平均值作為點的鄰域距離，剔除339個點。計算結果與原始數據相比較可以發現，在點云數據下方已不存在離群點，但也在數據中出現空白區域。圖3（c）和圖3（d）分別是采用LOF和LDOF算法對原始點云進行離群點檢測的效果，算法中的K鄰近點取值均為8，剔除離群點數分別為22和19，在點云的下方還存在比較多離群點。

從圖3（a）中可以發現，該部分點云數據中不但包含了零散的離群點，還包括由于光滑表面影響產生的離群點團。對于在點云中的離群點團，如果采用目前比較熱門的局部離群點檢測方法，如LOF和LDOF不能很好的將所有的離群點檢測出來，如圖3（c）和圖3（d）的效果所示。采用本文的算法不僅能將零散的離群點檢測出來，同時還能將離群點團也檢測出來，效果如圖3（b）。

二）不同類型K鄰域距離的比較

在本算法中，點與點之間的距離可以通過歐氏距離或曼哈頓距離進行計算，同時任一點的K鄰域距離可以通過計算該點到K鄰域中K個點的平均距離或最大值距離算取。如表1是在某包含45000體素的點云中，當K=8時，采用不同距離組合算法檢測出離群點的個數、比例和運行時間。

從表1可以發現，根據本算法思路采用不同距離算法檢測結果雖相近，但也存在可循規律的不同。首先采用最大值計算K鄰域距離比采用平均值檢測出的離群點稍多，其主要是因為最大值計算K鄰域距離將真正離群點鄰域內的所有點都認定為離群點。比如歐氏距離時，采用最大值檢測到358個離群點，而均值檢測的離群點為339，對應離群點比例分別為0.8%和0.75%;曼哈頓距離計算點與點距離時，采用最大值檢測到364個離群點，而均值檢測到的離群點為348，對應離群點比例分別為0.81%和0.77%。其次采用馬哈頓計算點與點之間的距離在時耗方面比采用歐氏距離比較少，主要原因是曼哈頓距離是一次方運算，而歐氏距離是二次方運算。同樣采用均值法計算K鄰域距離時，曼哈頓距離花費時間比歐氏距離少1.13秒，而最大值法的則少0.87秒。

三）K值的影響

該部分實驗主要驗證K值對文中算法的影響，如表2同樣是在某包含45000體素的點云中，當采用曼哈頓一最大值的K鄰域距離時，在不同K值的情況下的離群點檢測結果。

首先從表2中可以清楚的發現隨著K值的增加，不管檢測到的離群點還是所耗費的時間都是隨之增加的。其次根據正態分布的3u定理，當K鄰域距離在3倍方差范圍內的分布概率為99.74%，超出該范圍的數值可以被認定為是離群，即有0.26%的點是離群點。表2中即使最小的K值對應的離群點比例都已超出了理論值，說明算法不但將離群點檢測出，還將少部分非離群點也認定為離群點，但所占比例不高，特別當K值比較小時。

4 結論

針對有序紋理點云數據中離群點檢測的問題，由于點云在X-Y平面坐標的有序和間隙相等的特征，提出根據點K鄰域距離的正態分布概率情況，判斷該點是否為離群點的算法。K鄰域距離由該點到K鄰域中每個點的歐氏距離或曼哈頓距離的平均值、加權值或最大值，根據正態分布的30-定理，如果K鄰域距離處在3倍方差范圍外，將被認定為是離群點。

由于皮革表面光滑等原因，實驗室掃描設備獲取的皮革紋理點云數據中存在離群點，使用該點云數據對文中提出的算法進行了三次實驗進行驗證。第一個實驗中與傳統檢測算法LOF和LDOF進行檢測效果比較，當K=8，傳統算法的不能檢測所有離群點的情況下，而文中算法能將所有離群點檢測出來。傳統算法效果不佳主要有兩個原因，一是傳統算法采用K最近鄰算法，是空間中的最近點，而本算法的K鄰域是X-Y平面坐標內的鄰域，是有序點云的最近點。二是傳統算法是基于空間密度的檢測算法，當離群點團內的點數大于K值時，該離群點團將視為正常點云。本算法對離群點團的判斷并不直接取決于K值，而是只要該點的K鄰域內有一個是正常點，則可檢測為離群點。

第二個實驗是不同類型K鄰域距離的比較，算法中需要計算點與點之間的距離和點到K鄰域距離。當點與點之間的距離為曼哈頓距離時所檢測到的離群點比歐氏距離多，其主要原因是當Z軸方向的值變化時對曼哈頓距離的影響比歐氏距離大。當使用最大值計算點到K鄰域的K鄰域距離檢測出的離群點比使用平均值所檢測的離群點多，因為只要點的K鄰域中存在一個離群點，該點就會被檢測為離群點。 K值是算法中唯一需要預先設定的參數，該參數跟K最近鄰算法中的K值選擇有所不同，K最近鄰算法中的K值可以是任一自然數，而本算法中的K值為4、8、16或24。從最后一個實驗的結果和分析可知，即便K值取最小值4時，所檢測出離群點的比率已超出理論分布值。

通過上述對本算法的討論，主要有如下特點：

1）本算法適用于有序點云數據中的離群點檢測;

2）采用K鄰域代替傳統的K最近鄰算法;

3）離群點判斷的依據是所有點的K鄰域距離大小符合正態分布。

在實驗結果中發現算法亦有不盡人意的地方，比如兩點之間的距離需要計算兩次，特別是采用歐氏距離計算，將耗費大量的時間;其次就是某正常點的K鄰域如果存在離群點，那么該點也可能被判定為離群點，出現過度檢測的問題。接下來將就有關方面繼續進行研究，將本算法進一步優化。

參考文獻

[1]孫寧.線狀動物紋理特征及其皮革面料設計應用[J]中國皮革，2016（03）：64-68.

[2] OJALA T， PIETIKAINEN M，MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binarypatterns[J]. Ieee Transactions on Pattern Analysis and MachineIntelligence， 2002， 24（7）：971-987.

[3]賀福強.大面積皮革表面的視覺檢測技術與應用研究[D].杭州：浙江大學，2012.

[4] MANJUNATH B S，MA W-Y. Texture features for browsing andretrieval of image data[J].Ieee Transactions on Pattem Analysisand Machine Intelligence， 1996， 18（8）：837-842.

[5]張建鵬，新型皮革紋理掃描儀控制系統的設計與實現[D].成都：電子科技大學，2014.

[6]CULAOG，DANAK J.3D texture recognition using bidirectionalfeature histograms[J].International Joumal of Computer Vision，2004，59（1）：33-60.

[7]HAWKINS D M.Identification of outliers[M].Vol. 11， Springer，1980.

[8]FILZMOSER P.Identification of multivariate outliers：A perfor-mance study[J]. Austrian Journal of Statistics，2016，34 （2）：127-138.

[9]PIT-CLAIDEL C， MARIET Z， HARDINC R.Outlier detection inheterogeneous datasets using automatic tuple expansion [OL].Technical Report MIT -CSAIL -TR -2016 -002， CSAIL， MIT， 32Vassar Street， Cambridge MA 02139 February 2016.

[10] SHEVLYAKOV G，SMIRNOV P. Robust estimation of the corre-lation coefficient： An attempt of survey[J]. Austrian Journal ofStatistics， 2016， 40（ 1&2）： 147-156.

[11] AKOGLU L， TONG H， KOUTRA D.Graph based anomaly detec-tion and description：A survey [J]. Data Mining and KnowledgeDiscovery， 2015， 29（3）：626-688.

[12]CHANDOLA V，BANERJEE A，KUMAR V.Anomaly detection：A survey [J]. ACM Computing Surveys

（CSUR）， 2009， 41（3）： 15.

[13]薛安榮，鞠時光，何偉華，等，局部離群點挖掘算法研究[J]計算機學報，2007（08）：1455-1463.

[14]薛安榮，姚林，鞠時光，等.離群點挖掘方法綜述[J]計算機科學，2008（11）： 13-18+27.

[15]劉靖，復雜數據類型的離群檢測方法研究[D].廣州：華南理工大學，2014.

[16] HA J， SEOK S， LEE J-S.A precise ranking method for outlier de-tection[J]_Information Sciences， 2015， 324： 88-107.

[17]HIDO S， TSUBOIY， KASHIMAH，et al.Statistical outlier detec-tion using direct density ratio estimation [J]. Knowledge and In-formation Systems， 2011， 26（2）：309-336.

[18] KNORREM，NCRT，TucakovV. Distance-based outliers： algo-rithms and applications[J].The VLDB Journal-The InternationalJournal on Very Large Data Bases， 2000，8（3-4）： 237-253.

[19] ZHANG K， HUTTER M， JIN H.A new local distance-based out-lier detection approach for scattered real-world data[C]. in Pacif-ic-Asia Conference on Knowledge Discovery and Data Mining，Springer.2009.

[20] BREUNIC M M，KRIEGEL H-P， NC R T，et al.Lof： Identifyingdensity-based local outliers[C].in ACM Sigmod Record ，ACM，2000.

[21] BHA'ITACHARYA G，GHOSH K，CHOWDHURY A S.Outlierdetection using neighborhood rank difference[J].Pattern Recog-nition Letters， 2015， 60： 24-31.

[22]DANESHPAZHOUH A， SAMI A.Semi-supervised outlier detec-tion with only positive and unlabeled data based on fuzzy cluster-ing [J]. International Joumal on Artificial Intelligence Tools，2015，24（03）：1550003.

[23] CHEN Y，DANG X，PENG H，et al.Outlier detection with thekemelized spatial depth function[J].Ieee Transactions on PatternAnalysis and Machine Intelligence， 2009， 31（2）：288-305.

[24]黃旺華，王欽若，徐維超，等，對椒鹽噪聲穩健的數字圖像斯皮爾曼秩次相關法[J].光學精密工程，2015，23（6）：1800-1806.