含有兩個隨機變量的二維幾何模型建構(gòu)探討

何雙

[摘要]幾何模型是高職數(shù)學(xué)的難點問題，幾何概率模型構(gòu)造的重點為如何使用測度。具有兩個隨機變量的二維幾何模型為高職階段中較為普遍的問題，利用練習(xí)直角三角坐標(biāo)系，創(chuàng)建平面圖像，將面積作為測度，能夠使此問題得到解決。就高職數(shù)學(xué)幾何模型建構(gòu)開展探討.供大家交流。

[關(guān)鍵詞]隨機變量;二維幾何模型;高職教學(xué)

[中圖分類號]0211.2

[文獻標(biāo)志碼]A

[文章編號]2096-0603（2019）07-0138-02

幾何模型屬于高職數(shù)學(xué)中重要的概率模型，在高職命題中具有重要的地位。解決二維幾何模型中的問題，重點就是尋找相應(yīng)區(qū)域中的面積，之后通過幾何模型概率公式實現(xiàn)計算。比如數(shù)形結(jié)合也是解決幾何模型問題的主要策略。幾何模型的主要特點就是實驗結(jié)果無限性及每個實驗結(jié)果出現(xiàn)等可能性。在隨機實驗中，假如具有兩個隨機變量，并且此隨機變量在兩個無限個值區(qū)域范圍中取值，此種隨機試驗?zāi)軌騽?chuàng)建將測度作為面積的二維幾何模型。二維幾何模型問題中的知識點比較多，題目也較為靈活，一般都是根據(jù)二元一次不等式組尋找區(qū)域面積，使用幾何化手段進行解決。

一、二維幾何模型中的幾何度量原則

（一）等可能性原則

在選擇幾何度量之后，單位尺度幾何度量指的是相同的事件數(shù)。因為使用幾何模型處理概率問題具備一定的等可能性特點，以此要求選擇的幾何度量都能夠均勻的代表所考察的事情，也就是滿足尺度均勻原則。

（二）主動性原則

因為使用特定幾何量實現(xiàn)事件的有效模擬，在實際問題中對如何完成此件事情比較關(guān)心，一般將考察事件模擬成為某個明確具體過程，并且主動完成考察元素。比如，使點在線段中運動，點在平面中，使點在圓弧中運動，直線圍繞頂點運動等，此種模擬及類比對題目的理解及解答是非常有利的。

二、兩個隨機變量的二維幾何模型分析

（一）區(qū)間長度中的兩個隨機變量

此種題目較為簡單，但是如何轉(zhuǎn)變成為數(shù)學(xué)模型進行求解為解決此種問題的重點。

例1：在區(qū)間[-1，1]中任意選擇兩個實數(shù)，那么其和大于1的概率為（）

分析：任意選擇的兩個數(shù)的實驗結(jié)果有無限個，出現(xiàn)基本事件為等可能，能夠滿足幾何模型條件。所以，假設(shè)在[-1，1]中任意選擇兩個實數(shù)作為x.y，根據(jù)題意x+y≤1，尋找相應(yīng)的區(qū)域，求得面積比就能夠得到。

解題：假設(shè)在區(qū)間[-1，1]中任意選擇兩個實數(shù)x.y，使（x，y）作為平面中的點，實驗中的所有結(jié)果創(chuàng)建區(qū)域{（x，y）}-1≤x≤1，-1≤y≤1，詳見圖1。其指的是邊長為2的正方形，面積為2x2=4，其和小于1，并且{（x，y）x+y≤1}，其區(qū)域?qū)儆陉幱安糠郑娣e為4-0.5=3.5，所以概率為：構(gòu)成事件A的區(qū)域面積/試驗全部結(jié)構(gòu)構(gòu)成的區(qū)域面積=3.5/4=7/8。

例2：隨機使長為1單位的線段劃分成為三段，求得三段能夠構(gòu)成的三角形概率。

分析：根據(jù)題目的含義，假設(shè)隨機得到的兩段長度為x和y，三段為1-x-y，三段的長度要能夠滿足創(chuàng)建三角形條件。實驗結(jié)果等可能性及無限性滿足幾何模型的條件需求。

解題：假設(shè)劃分的兩段分別為x和y，那么第三段就是1-x-y，要滿足01-x-y，1-x>x，1-y>y的需求，其中的平面面積就是陰影的部分A，得到Sq=1/2*1*1=1/2，SA=1/2*1/2*1/2=1/8，那么P（A）=（1/8）/（1/2）=1/4。

以上兩個問題看起來具有三個變量，但是能夠?qū)⑵滢D(zhuǎn)變成為兩個變量。另外，還要注意相應(yīng)區(qū)域中的面積不包含邊界，但是不會對解決結(jié)果造成影響。

（二）和生活實際問題相互結(jié)合

例3：甲和乙兩個人約定在六點到七點之間在某個地方會面，并且約定先到的人要等候另外一個人一刻鐘，一刻鐘過去之后就能夠離去，求得兩個人能夠會面的幾率。

分析：甲和乙兩個人都是六點到七點中的任意一個時間段到達會面的地點，所以要引入到達時間x和y，也就是創(chuàng)建雙變量幾何模型。

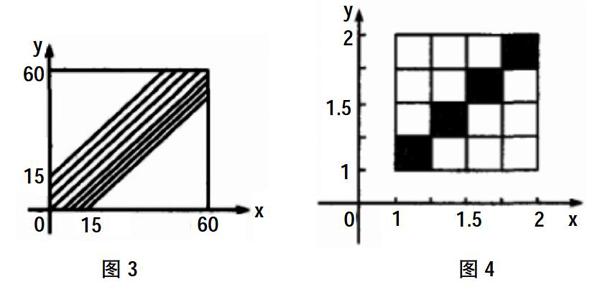
解題：將x指的是甲到達約定地點的時間，y指的是乙到達約定地點的時間，那么0≤x≤60，0≤y≤60，在圖3中的平面直角坐標(biāo)系中的點（x，y）對應(yīng)邊長為60的正方形記做甲和乙兩個人能夠會面的事件A，那么滿足|x-y|≤15的條件需求，點（x，y）所對應(yīng)的就是圖中的陰影部分，通過幾何概率公式得到P=（603-452）160=7/16，那么甲和乙能夠會面的概率就是7/16。

此種題目的難點就是使用兩個時間分別表示x和y，創(chuàng)建平面中的點（x，y），以此能夠?qū)r間長度問題轉(zhuǎn)變成為二維平面圖形面積問題，結(jié)合二維幾何模型就能夠求解。

例4：甲和乙兩個人約定在下午一點到兩點之間到某個車站起乘坐公共汽車去逛街，在此時間段中的公共汽車班次一共有四班，發(fā)車的時間分別為一點十五分、一點三十分、一點四十五分和兩點整，假如在規(guī)定時間上車，求兩個人乘坐同一輛公共汽車的概率。

解答：假設(shè)甲和乙到達車站的時間分別是x和y，那么1≤x≤2，1≤y≤2，對平面S進行確定，詳見圖4中的正方形區(qū)域，假設(shè)事件A指的是同個人乘坐同一輛公共汽車，那么事件A中的充要條件就是兩個人到達時間x和y都是在同個發(fā)車區(qū)間中，也就是圖中的陰影部分，所以P=4/16=1/4。

（三）二維幾何模型中的事件獨立性

例5：假設(shè)實驗E指的是拋甲和乙兩枚硬幣，對正反面的出現(xiàn)情況進行觀察。如果A指的是甲硬幣的出現(xiàn)H，事件B指的是乙硬幣的出現(xiàn)H，那么E樣本空間就是：02=（{HH，HT，TH，TT}

通過此可以看出來：P（A）=2/4=1/2

P（B）=2/4=1/2

P（A|B）=1/2

P（AB）=1/4

在整個過程中的P（A|B）為P（A），P（A B）為P（AB）=P（A）P（B），也就是事件B發(fā)生對于事件A并沒有什么影響，此并不是偶然。通過題目含義可以看出來，甲硬幣正面的出現(xiàn)情況和乙?guī)懦霈F(xiàn)正面的情況是沒有什么影響的。

假設(shè)事件A和事件B，如果P（AB）=P（A）P（B），那么事件A和事件B是相互獨立的。如果四對事件A和B，A和B，A和B，和中有一個是對立的，那么其他三對也是獨立的。

證明：因為對稱性，只要通過A和B獨立導(dǎo)出另外三對獨立就行，通過條件，得到：P（AB）=P（A）P（B）

所以：P（AB）=P（B-AB）=P（B）-P（AB）

=P（B）-P（A）P（B）

=P（B）[1-P（A）]

=P（B）P（A）

那么可以看出來，A和B都是相互獨立的，以此也就表示A和B也是相互獨立的。因為A=A，那么A和B相互獨立。

在實際使用過程中，不能夠使用定義對事件獨立性進行證明，要以具體的問題情況，根據(jù)獨立性實際意義進行判斷。另外，獨立性概念還能夠應(yīng)用到多事件中。

首先，對三個事件進行定義，A和B和C都具備獨立性，如果以下公式同時成立，那么就表示A和B和C都是相互獨立：P（AB）=P（A）P（B）

P（BC）=P（B）P?

P（AC）=P（A）P?

P（ABC）=P（A）P（B）P?

以事件獨立性定義表示，前三項的等式成立，那么A和B、B和C，C和A都是相互成立的，也就是A和B和C都是兩兩獨立。但是，兩兩獨立也不能夠保證都是相互獨立。

（四）基于貝特朗問題

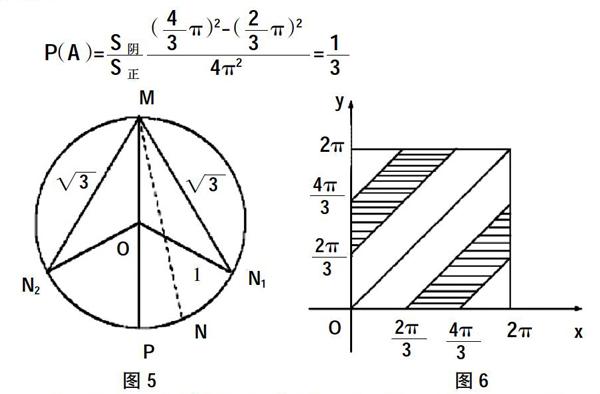
貝特朗問題指的是在單位圓的圓周中，任意選擇兩個點M和N聯(lián)結(jié)成弦，事件A指的是弦長MN>V3，求解事件A的發(fā)生概率。

解題：此圓的周長為2π，在圓中任意取一個點，設(shè)置其位置為0，圓中的其他各個點位置根據(jù)順時針方向在[0.2π）中增長。假設(shè)M和N在圓周中的位置分別為x和y，那么x.y∈[0.2π），詳見圖5。MN>V3當(dāng)且僅當(dāng)2/3 π<（x-y|<4/3 π，詳見圖6。使用（x，y）將實驗結(jié)果表示出來，那么全部基本事件創(chuàng)建正方形區(qū)域，其中的陰影部分指的是事件A創(chuàng)建的區(qū)域，滿足幾何模型條件需求，所以：

本道題的解法就是基于題目原始條件，在圓周中選擇兩個點作為等可能事件，并且引入兩個變量，以此將面積作為測度，使用幾何模型理論得出答案，較為簡單，并且不容易出錯。

三解題規(guī)律

根據(jù)本文解法的規(guī)律，將具備兩個隨機變量二維幾何模型問題的解題方法總結(jié)為：

其一創(chuàng)建變量。通過題意，對哪兩個變量為隨機，將其設(shè)置成為x和y;

其二，將不等式組列出。根據(jù)題意得到兩個變量，從而使條件不等式得到滿足;

其三，做出平面區(qū)域。做出上述不等式組的平面區(qū)域;

其四，對區(qū)域面積進行計算。以作出的平面區(qū)域，對相應(yīng)區(qū)域面積進行計算;

其五，面積比值求解。以幾何模型公式，得到兩個面積的比值。

四、結(jié)語

幾何模型就是結(jié)合幾何問題及概率問題，對此種問題進行有效解決，重點就是全面理解題目意思，尋找變量和變量之間的內(nèi)在關(guān)系，從而得到變量滿足不等式組。之后利用不等式組中的平面區(qū)域得到需要的測度。其中.數(shù)形結(jié)合指的是對此種問題有效解決的主要思想方法。

參考文獻：

[1]程海奎，陳雪梅.是強調(diào)幾何度量還是關(guān)注概率模型的建構(gòu)：關(guān)于幾何概型教學(xué)的再思考[J].數(shù)學(xué)通報，2014，53（11）：26-29.

[2]王穎穎，霍睿，李明珠，等.隨機事元和可拓變換在二維隨機變量分布模型研究中的應(yīng)用[J].中國設(shè)備工程，2017（7）：177-179.

[3]汪俊超.構(gòu)建幾何模型解立體幾何問題[J].中學(xué)生數(shù)理化（學(xué)習(xí)研究），2013（3）：20.

[4]邢存恩，張明祿，韓傳廷，等.二維幾何作圖法借助三維模型設(shè)計采區(qū)中部車場的探討[J].太原理工大學(xué)學(xué)報，2012，43（2）：180-184.

[5]張爽，吳曉青，程勇.二維編織理論研究進展[J].玻璃鋼/復(fù)合材料，2017（8）：102-109.

[6]陳海庭構(gòu)建“圖形與幾何”數(shù)學(xué)模型的策略[J].福建基礎(chǔ)教育研究，2016（3）：104-105.

[7]孫丹.建構(gòu)主義理論指導(dǎo)下的初中幾何圖形變換模型教學(xué)策略研究[J].商，2014（45）：256.

[8]陳永晶.集合模型.幾何圖模型和曲線模型在高職生物學(xué)教學(xué)中的應(yīng)用研究[D].廣西師范大學(xué)，2016.

[9]張和平.基于結(jié)構(gòu)方程的幾何直觀能力測評模型構(gòu)建[J].貴州師范大學(xué)學(xué)報（自然科學(xué)版），2017，35（2）：104-108.