數學建模思想融入下的民辦院校線性代數課程教學改革研究

卜令杰

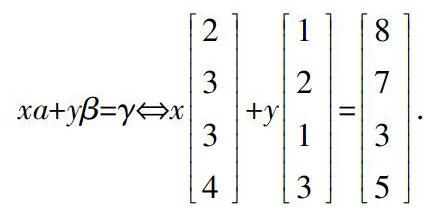
[摘? ? ? ? ? ?要]? 通過對民辦院校線性代數課程的教學實況進行分析，反思當前的線性代數教學方法，進而得出將數學建模思想融入線性代數教學的必需性，并給出了將數學建模思想融入線性代數教學過程的方法。

[關? ? 鍵? ?詞]? 數學建模;線性代數;教學改革

[中圖分類號]? G642? ? ? ? ? ? ? ?[文獻標志碼]? A? ? ? ? ? ? ? ? ? ? ? [文章編號]? 2096-0603（2019）04-0206-02

一、民辦院校線性代數課程的教學實況

線性代數是我國高等院校一門尤為重要的基礎理論課，它在培養學生邏輯思維能力、抽象問題及實際問題的解決能力等方面有著尤為重要的作用。但大多線性代數教材僅僅注重知識的傳授，且將理論知識邏輯推導都介紹得非常非常的詳盡細致，但卻極度缺少線性代數知識在解決實際問題的例子。與之對應的，大多民辦院校的線性代數教學也是以理論性教學為主，課堂上幾乎都是數學知識的傳授及其邏輯推理，這樣的教學方法使學生在學習時只是機械、枯燥地計算，很難和知識的實際應用結合起來，導致學生認為該門課程沒有用，只是為完成學分而學，不考研根本用不上。為改變這種教學狀態，極需對現在的線性代數課程進行教學改革[1-4]。

數學模型是用數學符號、數學式子、程序、圖形等對實際課題的本質屬性進行抽象而又簡潔的刻畫，它或能解釋某些客觀現象，或能預測未來的發展規律，或能為控制某一現象的發展提供某種意義下的最優策略或較好策略。這種應用知識從實際課題中抽象、提煉出數學模型的過程就稱為數學建模。

大多數學建模試題都取材于生活實際，例如：一個企業要生產一種新的產品，應考慮如何計劃生產才能以最小的投入獲取最大的利潤。要解決此類問題，就要用到線性代數的相關知識，這種與生活及日后工作密切相關的問題能夠引起學生學習的興趣。通過對這種用線性代數知識解決實際問題例子的講解，可以使學生更容易體會到線性代數知識在解決實際問題中的用途。這樣不僅可以增強學生學習的興趣，同時也可以消除數學知識無用的觀點。因此，將數學建模的思想引入線性代數課程的日常學習中就顯得非常有必要。

所以為了彌補傳統線性代數知識學習的乏味，提高學生學習線性代數的積極性，培養學生利用數學相關知識解決實際問題的能力以便更快、更好地適應社會，我們有必要將數學建模的思想貫徹到線性代數知識的日常學習中。

二、數學建模思想融入線性代數的教學過程

（一）把數學建模思想融入線性代數定義的講解中

線性代數課程所涉及的很多定義，都是對現實生活中一些實際的問題進行歸納和概括得來的。因此，對這些定義進行講解時，可以借助歷史背景以及其在生活實際中的應用等對其歸納和概括的過程進行分析，引導學生感知定義得出的整個過程，使學生認識到數學源于生活，逐步樹立數學建模思想，養成觀察生活的習慣，更好地利用數學知識去解決生活實際問題。比如，在求解空間多面體模型體積的過程中可以借鑒他人的求解過程，從平行四邊形和空間六面體體積出發，得到2階和3 階行列式的基本公式，從而引起學生對定義和公式的推導興趣。在有了模型的前提下，就有了實際應用的背景，學生在學習過程中的目的性也會更加明確[5]。

線性相關性是線性代數課程中的核心定義，深刻理解和掌握這兩個定義對整個線性代數知識的學習都尤為重要。然而向量組的線性相關、線性無關理論較抽象，我們可以利用數學模型來幫助學生理解這組定義。

例：在化工、醫藥等方面都常常會遇到調配問題。比如：某種組合材料由四種原料混合而成。但是該組合材料現僅有兩種不同規格，且四種原料的組合比例分別2∶3∶3∶4和1∶2∶1∶3。但是現在需要四種原料的比例為8∶7∶3∶5的另一種規格的材料。 問：第三種規格的組合材料料能否由前兩種規格的組合材料按一定比例組合配制而成[6]？

假設種成分之間不會發生某些化學反應，則材料配比問題可以用向量來建模。假設前兩種規格的材料分裝成袋，比如說第一種規格的材料每袋凈重12g（其中四種原料分別為2g、3g、3g、4g），第二種規格的材料每袋凈重7g（其中四種原料分別為1g、2g、1g、3g）。

根據已知數據和上述假設，可以進一步假設將x袋第一種規格的材料與y袋第二種規格的材料混合在一起，得到的混合物中四種原料分別為8g、7g、3g、5g，則有以下的關系，實際是討論向量α，β，γ是否線性相關，進一步討論γ能否由α，β線性表示。

xa+yβ=γ？圳x2334+y1213=8735.

（二）把數學建模思想融入線性代數例題的講解中

在例題講解過程中融入數學建模思想，無論對教師講解還是學生理解都是非常有幫助的，在理論知識的講解過程中引入一些現實中的相關問題，教師通過自己的講解引導學生主動去分析，在分析過程中可以提出假設，在驗證假設合理之后建立相應的數學模型，這不僅是對問題的一個求解過程，更是處理現實問題的一種有效手段。此種解決問題方法的運用能使學生明確感受到在對現實問題的解決過程中線性代數的重要作用。

特征值問題是線性代數中比較抽象難懂的，一般教科書都是從矩陣對角化等抽象問題來引進，我們通過實例讓學生進一步理解矩陣對角化的應用。比如：講授矩陣的對角化時引入數學模型案例——對城鄉人口流動作年度調查，發現居民有一個穩定的朝向城鎮流動的趨勢：每年農村居民的2.5%移居城鎮，而城鎮居民的1%遷出。現在總人口的60%位于城鎮。假如城鄉總人口保持不變，并且人口流動的這種趨勢繼續下去，那么一年以后住在城鎮的人口所占比例是多少？兩年以后呢？十年以后呢？最終呢？

例[7]：在講解矩陣乘法和逆矩陣知識時可以給學生講解密碼問題如下：

把A、B…等26個大寫英語字母與數字1、2、3、…、26建立1-1對應即：A-1，B-2，C-3，…，Z-26。想要發送信息PERFECT，按照編碼規則，只需發送16、5、18、6、5、3、20共7個代碼即可。接收信息的人根據編碼規則，就可以譯出發送過來的信息。但是，這種做法信息的安全性不高，很容易被破譯。這樣，我們可以利用矩陣乘法和逆矩陣對所要傳送的消息進行加密。例如，按編碼規則，發送信息GOOD。

首先將要發送的信息按照接收到的順序兩兩組合，則據編碼規則，每組字母都對應一個列向量，即（G，O）T=（7，15）T，（O，D）T=（15，4）T;

其次取一個2×2的可逆陣，若取A=2 11 1，其逆陣為：A-1=1 -1-1 2。

下面用矩陣A左乘每一個列向量：A（G，O）T=2 11 1715=2922，A（G，O）T=2 11 1154=3419。

因此只需發送代碼：29、22、34、19即可。而接受信息的人只需將接收到的信息按照接收的順序兩兩組成一個列向量，再分別左乘A-1即可還原信息：A-1=2922=1 -1-1 22922=715，A-13419=1 -1-1 23419=154;

最后根據編碼規則，即可還原為發送的真實信息為：GOOD。

通過線性代數知識與實際應用的結合來講解線性代數例題，可以使學生更加容易看到、體會到線性代數知識在解決實際問題中的用途，從而提高學生學習線性代數知識的熱情和興趣，進而消除學生頭腦中學習數學知識除了鍛煉思維而無其他用途的觀點。

（三）把數學建模思想融入線性代數課后的練習中

民辦院校線性代數教學內容側重于理論及機械的運算，大多數的課后習題只是為鞏固基礎知識和運算技巧而設置的，對線性代數知識的實際應用問題基本上沒有涉及，學生的實際應用訓練不夠，致使學生產生學習數學知識無用論，因此適當地補充一些簡單的線性代數建模習題是非常有必要的，這樣既可讓學生進一步理解和鞏固所學知識，也可讓學生把所學的知識與數學建模思想方法相結合起來解決實際問題、學以致用。

參考文獻：

[1]孫玉泉.關于工科數學教學與專業培養融合的探索[C]//大學數學課程報告論壇組委會.大學數學課程報告論壇論文集2011.北京：高等教育出版社，2011：1-4.

[2]李繼成.線性代數與空間解析幾何課程全面改革的思考[J].大學數學，2010，26（2）：7-10.

[3]李大潛.將數學建模思想融入數學類主干課程[J].中國大學教學，2006（1）：9-11.

[4]李尚志.線性代數教學改革漫談[J].教育與現代化，2004（1）：30-33.

[5]睢音.試析如何在線性代數教學中融入數學建模思想[J].吉林省教育學院學報，2014（3）：60-61.

[6]朱婧，胡志興，劉正.線性代數教學中融入數學建模思想的探索[J].2014（4）.

[7]魯鑫.數學建模在應用型本科“線性代數”教學中的應用探索[J].宿州教育學院學報，2017（3）：148-149.

編輯 馬燕萍