滲透數學思維培養的課堂教學研究

王紅根

摘要 數學教學是思維活動的教學，而不只是數學知識的教學。學生的思維發展是數學課堂教學的關鍵。基于此，以“等腰三角形分割”一課為例，從思維的廣博性、延續性、嚴密性和批判性出發，闡述如何在數學課堂教學中有機滲透學生數學思維的培養。

關鍵詞 數學思維 課堂教學 等腰三角形 分割

一、問題提出

通常我們都認為思維是智力的核心，那思維的培養無疑是教育的本質目的之一。著名教育家贊可夫指出：“在各科教學中要始終注意發展學生的邏輯思維，培養學生思維的靈活性和創造性。”而思維活動的教學恰好體現在數學課堂中，學生思維的發展是教師數學教學的核心目的。可以說，沒有數學思維，就沒有真正意義上的數學學習。因此培養學生的數學思維是很有必要的。

基于培養思維的必要性和重要性，要求數學教師在課堂教學中注重對學生數學思維的培養。下面以初中數學“等腰三角形分割”一課為例，闡述在課堂教學中滲透對學生數學思維的廣博性、延續性、嚴密性和批判性的培養。

二、數學思維的具體培養

1.思維的廣博性。

思維的廣博性是指對一個問題從多方面考慮，不要只做表面的觀察，而應由此及彼、由表及里地進行分析，不斷擴大觀察和思索的范圍。具體表現為對一個命題給出多方面的解釋，對一個對象用多種方式表達，對一個問題思考各種不同的解法。在數學教學中，教師要注重多方位、多角度的思考方式，拓廣解題思路，培養學生思維的廣博性。

問題1：任何三角形都能夠被分成兩個等腰三角形嗎？

生1：對于我們學過的等腰直角三角形，作斜邊上的高可以把它分成兩個等腰三角形。

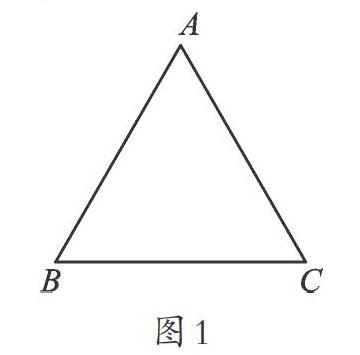
生2：正三角形應該也可以（如圖1）。

稍息片刻后全班愕然：正三角形這么特殊，居然不能被分成兩個等腰三角形？

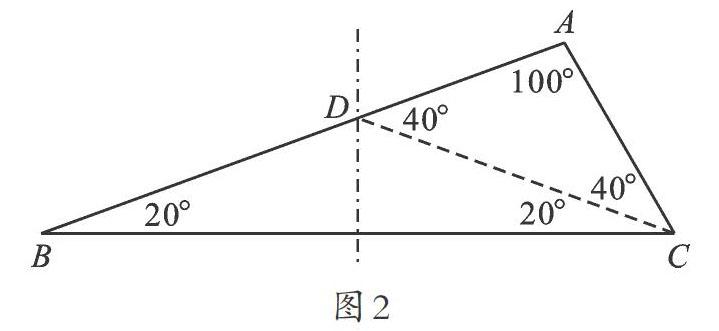
師：是不是只有特殊三角形才能被分成兩個等腰三角形呢？老師給大家舉個例子。如圖2，

∠A=100°，∠B=20°，∠C=60°。你能把這個三角形分成兩個等腰三角形嗎？

生3：動手嘗試，比較容易從60°角中“拆出”20°角和40°角，從而得到兩個小的等腰三角形，其實就是利用畫BC邊的中垂線可以得到分割線CD。

上面兩個例子說明，并不是特殊的三角形就能被分割成兩個等腰三角形，而圖2看似普通的三角形卻能被分割成兩個等腰三角形。

問題2：那么怎樣的三角形能夠被分割成兩個等腰三角形呢？即三角形能夠被分割成兩個等腰三角形要具備什么條件？

教師通過舉例，并由學生動口回答、動手操作，發現不只等腰三角形能分割成兩個小等腰三角形，繼續引導學生探究“怎樣的三角形能夠被分割成兩個等腰三角形”，注重引導學生發散性思維的培養。通過上面例子的提升，學生自然想到正三角形，這是定勢思維的體現，課堂上遇到該情況，教師可以及時給出提前準備好的例子，發散學生的思維以提升思維的廣博性。在課堂上的指導應該切合課題，不可脫離課堂進行發散思維。

2.思維的延續性。

思維的延續性表現在數學課堂教學過程中，教師通過“潤物細無聲”的引導，尊重學生的思維過程，在學生已有的知識和學習經驗的基礎上，保持學生思維順暢，循序漸進地進行教學，而不是“拔苗助長”，脫離實際教學。這也符合倡導多年的以學生為主體的新課程理念。

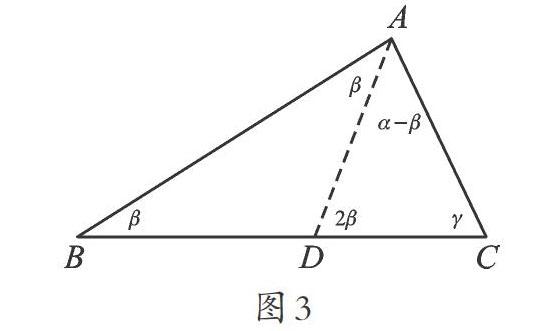
如圖3，設∠BAC=α，∠B=β，∠C=γ。線段AD將△ABC分成等腰三角形ABD和等腰三角形ACD。

幾何條件代數化。

師：請問，圖3中其他的角是否也可以表示出來呢？

生4：∠BAD=β（理由：AD=BD）。

生5：∠ADC=2β（理由：外角等于不相鄰內角之和）。

生6：∠DAC=α-β。

師：△ACD為等腰三角形有怎樣的情況呢？

生7：（情況1）有可能∠ADC=∠C，如圖4，即2β=γ①。

生8：（情況2）也有可能∠DAC=∠C，即α-β=γ②。

生9：還有可能∠ADC=∠DAC，即2β=α-β③。

師：請大家來解釋一下①②③各表示什么意思？

生10：①“2β=γ”表示原三角形有一個角是另一個角的2倍（Ⅰ）。

師：對于②“α-β=γ”說明了什么？

師：我們添加一個固有的條件：∠A+∠B+∠C=α+β+γ=180°④，可以發現什么呢？

生11：由②④可得2α=180°，即α=90°⑤，即原三角形是一個直角三角形（Ⅱ）。

生12：我知道③就是“α=3β”，表示原三角形有一個角是另一個角的3倍（Ⅲ）。

在上述教學片段中，用代數手段來解決幾何問題是數學的基本方法，它體現了數學的工具作用，體現了轉換、轉化的思想。這里學生可能不敢嘗試用三個字母來研究問題，此時教師要大膽鼓勵這樣的“建模”，這也為學生接下來的高中學習做好鋪墊。在初中數學學習中應該有許多的機會讓學生見識“建模”，運用“建模”，進而理解數學科學的作用。我們根據建立的模型發現了這里有三種可能的情況。這也是數學分類討論思想的體現。對于前面的三種情況，分別由學生得到3句概括的語句，從而提煉和初步抽象出能分割成兩個小等腰三角形的三角形該具備怎樣的3種不同條件。但是這只是猜想，具備這樣條件的三角形一定能分割成兩個小等腰三角形嗎？怎么分割呢？所以這里又提出了新的問題。這就是思維的延續性的體現。在課堂設問中，問題必須循序漸進，層層遞進，設置梯度，有效推進，“淺入深出”，正如教學片段中所呈現的設問方式，能夠提升學生思維的延續性，基本概括出本課題的模型，提升課堂深度和廣度。

3.思維的嚴密性。

思維的嚴密性是指學生考慮問題時，需要通過訓練達到嚴密、有據的地步。要提高學生思維的嚴密性，首先要求學生要思路清晰，就是要按照一定的邏輯順序思考問題。特別在學習新的知識與方法時，應從基本步驟開始，一步一步深入，不可用跳躍式思維。其次要求學生要全面、周密地思考問題，做到推理論證要有充分的理由作根據，這充分體現在幾何論證中。具體的體現是學生需要運用直觀的角度，但不停留在直觀的認識上;運用類比，但不輕信類比的結果;審題時不僅注意明顯的條件，而且留意發現那些隱蔽的條件;應用結論時注意結論成立的條件;仔細區分概念間的差別，弄清概念的內涵和外延，正確地使用概念;給出問題的全部解答，不使之遺漏。

（1）符合（Ⅰ）的三角形一定能夠被分割成兩個等腰三角形。

已知：在圖4中，∠ACB=2∠B=2β。

師：畫AD（也可以畫AB的中垂線與BC相交于D），使∠BAD=∠B=β。請問同學們，發現什么了嗎？

生13：∠ADC=2β，進一步有∠ADC=∠C，那么，△ABD和△ADC都是等腰三角形。

（2）符合（Ⅱ）的三角形一定能夠被分割成兩個等腰三角形。

已知：在圖5中，∠C=90°。

師：畫CD，使∠BCD=∠B=β能做到嗎？

生14：只要畫BC的中垂線就行了。

師：請同學們繼續想下去。

生15：這時∠ADC=2β。

生16：利用∠ACD與∠BCD互余，而且∠DAC與∠B互余，所以∠ACD=∠DAC，即△BCD和△ADC都是等腰三角形。

師：（Ⅲ）的證明與（Ⅰ）的證明是類似的。

在教學中要鼓勵學生做到大膽猜測，小心求證，而求證的過程正好是思維嚴密性的最好體現。該片段中，教師采用（Ⅰ）的證明過程作為范例，在討論過程中注重幾何問題代數化，證明一般情況下的結論，使得結論具有普遍性，便于推廣，充分反映了思維的嚴密性。嚴謹地推理是數學的一大優勢，是數學成為科學工具的重要特征。證明對于初三學生并不陌生，他們大多數能夠理解。模仿證明困難應該不會太大。學生對探索過程和提煉結論都是比較關注和感興趣的，但得到結論后，他們往往容易忽略對探索、猜想結論的證明，這點要引起教師注意。同時對自我探索結論的證明不僅能考查學生的數學分析、證明能力，還能較好地培養學生思維的嚴密性和深刻性。

4.思維的批判性。

數學知識具有嚴密的邏輯系統。在初中數學學習中，某些舊知識是新知識的基礎，新知識又是舊知識的引申和發展，學生的認識活動也總是以已有的舊知識和經驗為前提，在原有的基礎上進行推廣的。因此，教師在教學每一個新知識點時，都要盡可能整合有關的舊知識，利用已有的知識來搭橋鋪路，引導學生運用知識遷移規律，在獲取新知識的過程中發展思維。批判性思維意味著獨立思考，敢于質疑，不盲從權威，不唯上不唯書;意味著基于證據和數據得出結論、做出決策，實事求是，不隨意不主觀;意味著思維過程嚴謹縝密，推理合乎邏輯，不武斷不獨斷。

以下教學案例是在教學過程中，喜愛數學、愛動腦筋的初三學生提出的質疑。

生：如圖6，設∠BAC=36°，∠ABC=96°，∠C=48°。這時該怎么畫呢？

師：原來D點在外面！這種現象叫“外分”。應該說還有意外發生，它發生在遇到“鈍角”的時候。這個其實很像我們在學三角形內切圓時，其實還有“旁切圓”的道理。

這是課堂中的一個意外發現，真是一個亮點啊。喜愛數學、積極開動腦筋的初三學生其實已經具備一定的科學研究和探索的能力了。我們發現數學上的很多問題，并不存在什么最終的結果。所以要培養學生思維的批判性和創新精神，其實就是要對這樣看似完美的結論進行“較真”。教師也要大大鼓勵這樣的“較真”，要敢于對看似完美的結論挑戰，促進自我不斷完善，這就是思維的批判性的體現。同時思維批判性對教師有著更高的要求，必須不斷提升專業知識，備課時模擬學生思維進行大膽探究，才能應對課堂中提出的各類問題。

三、幾點思考

1.教材的深層把握是基礎。

具有思維的課堂應該是所有教師不懈追求的目標與方向，但是課堂不可脫離實際。初中生面對升學的壓力，使得課堂必須在把握教材的基礎上進行拓廣，一定要從教材全局觀和實質內涵來切入，不可脫離實際進行漫無目的的發散思維，違反了思維的嚴密性。同時要增加課堂的思維，必須充分挖掘、深層次挖掘題目背后的教材原型，這也契合當前中考題的思路。

2.學生的學習方式的轉變是關鍵。

課堂的主體一定是學生，教師是課堂的主導。在課堂中，如果學生沒有轉變學習方式，沒有參與到課堂的探究和學習中去，沒有體驗學習過程，則無法提升思維。學生的學習方式的轉變需要依靠教師從初一開始強調，在課堂中設計巧妙適合的學習活動，讓學生參與進來。學生學習方式轉變了，愿意跟隨教師的思路參與到課堂中間，教師的思維訓練才會起到關鍵性效果。

3.教師課堂指導藝術是保證。

轉變學生的學習方式以及對于教材的深層把握都需要教師具有扎實的專業知識和專業技能。其中非常重要的是對于課堂節奏的把握，在備課的過程中需要熟悉學生的知識水平和生活經驗，上課的過程中根據學生思維對課堂進度進行及時的調整和反饋，注重設問技巧以及與學生的交流，促進學生思維的發展。

（作者單位：浙江省杭州市建蘭中學）

【參考文獻】

[1]周紅斌.從特殊到一般 由結果探條件——也談一個三角形分割成兩個等腰三角形的條件[J].初中數學教與學， 2015（3）：30-32.

[2]吳桂余.關于一個三角形分割成兩個等腰三角形的討論[J].初中數學教與學， 2010（7）：25-26.

[3]王洪毅.初中數學思維能力的培養研究[J].時代教育， 2010（1）：148-148.

[4]王清.初中數學函數教學中數學思維能力培養的實證研究[D].長春：東北師范大學， 2005.