UR5機器人運動學及奇異性分析

張付祥 趙陽

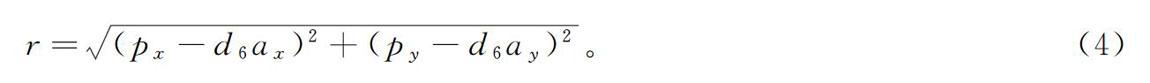
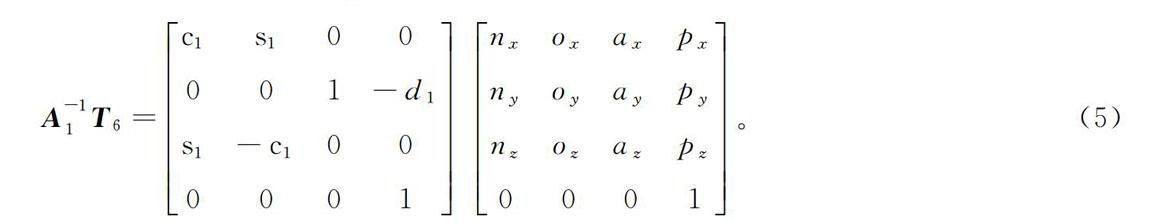
摘要：為了解決UR5機器人用戶建立的機器人坐標系與廠家建立的機器人坐標系不一致，機器人內部有關力、角速度、角加速度等數據信息難以被直接使用的問題，在分析UR5機器人結構特點的基礎上，建立與廠家數據匹配的坐標系。采用D-H參數法建立UR5機器人的運動學方程，描述機器人各桿件的相對位姿關系，依據UR5機器人滿足Pieper準則的結構特性，采用分離變量法求取UR5機器人的運動學反解，并利用微分變換法完成UR5機器人奇異位形分析，奇異性分析與仿真結果表明了UR5機器人位置奇異時各關節變量之間的關系。使用MATLAB軟件編寫運動學程序，并利用機器人系統對程序進行實驗室測試與工程實踐驗證，MATLAB運動學程序實驗結果與UR5系統內部數據一致，驗證了運動學分析的正確性。研究結果對進一步開展UR5機器人連續軌跡規劃研究具有參考價值。

關鍵詞：工業機器人技術;坐標系;運動學;微分變換法;奇異性

中圖分類號：TH122文獻標志碼：A

ZHANG Fuxiang， ZHAO Yang.Kinematics and singularity analysis of UR5 robot[J].Journal of Hebei University of Science and Techno-logy，2019，40（1）：51-59.Kinematics and singularity analysis of UR5 robot

ZHANG Fuxiang， ZHAO Yang

（School of Mechanical Engineering， Hebei University of Science and Technology， Shijiazhuang， Hebei 050018， China）

Abstract：In order to solve the problem that the UR5 robot coordinate system established by the user is inconsistent with the manufacturer's， and the data related to the force， angular velocity， angular acceleration are difficult to be directly used， based on the analysis of the structural characteristics of the UR5 robot， the coordinate system matching the manufacturer's data is established. The kinematics equation of the UR5 robot is established by D-H method to describe the relationship of each joint. According to the structural characteristics satisfying the Pieper criterion of the UR5 robot， the kinematic inverse solution of the UR5 robot is obtained by the separation variable method. The singularity analysis of UR5 robot is completed by differential transformation method， and the singularity analysis and simulation results show the relationship between the joint variables of UR5 robot when the position is singular. The kinematics program is written by using MATLAB software， and the robot system is used to carry out laboratory test and engineering practice verification. The experimental results of MATLAB kinematics program are consistent with the internal data of UR5 system， which verifies the correctness of kinematics analysis. The research result has some reference for further research of UR5 robot continuous trajectory planning.

Keywords：industrial robot technology; coordinate system; kinematics; differential transformation; singularity

隨著中國制造強國戰略第1個十年行動綱領“中國制造2025”的提出與實施，機器人在各行各業中的應用率日益攀升。串聯機器人作為一種典型擬人化機電設備，以其結構簡單、控制簡單、運動空間大且靈活等特點[1-3]被廣泛應用在焊接、噴漆、涂膠、搬運、裝配等領域[4]。UR5機器人是丹麥Universal Robots公司[5]推出的新型人機協作機器人[6]，它具有快速、靈敏、安全、重量輕以及易于編程等優點[7]。作為一款新型的六自由度機器人，它能實現6個關節360°旋轉，比普通的六自由度機械臂擁有更大的操作空間，同時具有更好的動力學優點和避障特性[8]。

河北科技大學學報2019年第1期張付祥，等：UR5機器人運動學及奇異性分析隨著UR系列機器人在國內應用越來越廣泛，眾多國內學者逐漸關注該系列機器人并進行研究。文獻[7—10]中建立了各自的UR機器人運行學坐標系，給出了相應的結構參數并用實驗驗證了各自結果的正確性。但上述文獻中建立的機器人坐標系與廠家建立的機器人坐標系并不一致，這就導致在他們各自坐標系下描述的機器人位姿與廠家描述的機器人位姿不符。由于用戶和廠家機器人坐標系的差異，從機器人系統內部讀取的力、角速度、角加速度等數據信息與用戶建立的機器人坐標系下的數據不匹配，從而導致機器人內部信息無法使用。在機器人軌跡規劃等高級應用時，由于坐標系的差異，用戶不能直接使用機器人關節信息求取機器人某一時刻的位姿，也不能利用UR機器人操控系統中的機器人位姿信息和用戶自行求解的逆向運動學表達式求解機器人關節變量。在目標位姿數目較少的工程應用中，可以通過示教模式進行點對點的操作，但要對機器人進行連續軌跡規劃時就會變得非常繁瑣與不便。為了解決上述問題，筆者在分析UR5機器人結構特點的基礎上，建立與機器人廠家數據匹配的機器人坐標系，并完成機器人奇異位形分析。研究結果可為UR5機器人的高級應用提供參考。

1UR5機器人正向運動學

1.1UR5機器人坐標系建立

UR5機器人由6個轉動關節組成，包括腰部、肩部、肘部以及3個自由度的腕關節。由于Universal Robots公司并未提供UR5機器人的坐標系，為便于機器人各種傳感信息的調用以及未來的高級應用，需要建立與UR5廠家相一致的機器人坐標系，進而掌握UR5機器人關節空間與笛卡爾空間的聯系。

D-H參數法建立機器人桿件坐標系的方法有兩種：第1種桿件坐標系與第2種桿件坐標系[11]。按照前者建立坐標系時，相鄰2個桿件（i-1）與i的桿件坐標系{i-1}與{i}都固定在桿件的關節編號大的關節處，而后者坐標建立方式與前者相反，坐標系固定在桿件編號小的關節位置處。采用第1種連桿坐標系建立方法建立UR5機器人坐標系，機器人各關圖1UR5機器人坐標系

Fig.1UR5 robot coordinate system節初始轉角與機器人實際初始轉角不符，機器人末端的位姿矩陣也與機器人系統描述的位姿矩陣不同。采用第2種連桿坐標系建立方法建立UR5機器人的坐標系，并依據UR5機器人系統提供的初始位置關節角度以及各關節運動方向對坐標系進行調整，最終建立起和廠家數據匹配的UR5機器人坐標系如圖1所示。

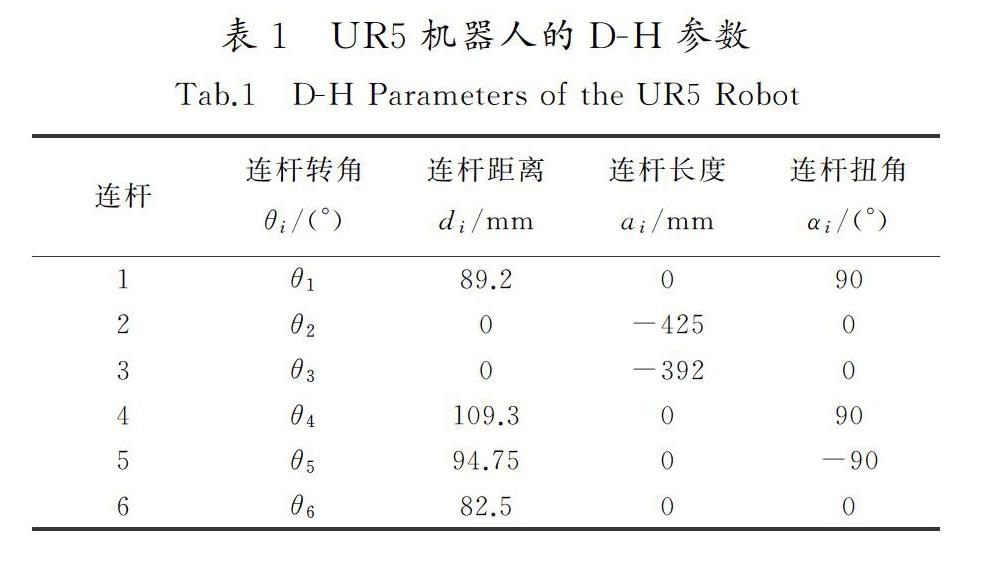
圖1中，為減小機構偏心對位姿矩陣精度造成的影響，將固聯在桿件2上的坐標系{2}移動至與坐標系{1}相重合。根據建立的UR5機器人坐標系，確定UR5機器人的D-H參數如表1所示。

1.2正向運動學方程

相鄰2個坐標系之間的齊次變換矩陣可用An表示[12]，其表達式如下：An=Rot（z，θn）Trans（0，0，dn）Trans（an，0，0）Rot（x，αn）。式中：Rot（z，θn）表示繞z軸旋轉了θn角;Trans（0，0，dn）表示沿z軸平移了dn個單位;Trans（an，0，0）表示沿x軸平移了an個單位;Rot（x，αn）表示繞x軸旋轉了αn角。為了簡化三角函數符號，以sθn表示sin θn，cθn表示cos θn，sαn表示sin αn，cαn表示cos αn。相鄰2個坐標系之間的齊次變換矩陣可表示為An=cθn-sθncαnsθnsαnαnc

0001。依據上式，可以計算出UR5機器人各個連桿坐標系之間的齊次變換矩陣A1—A6如下： A1=c10s10

A1—A6中si表示sin θi，ci表示cos θi，ai，di對應表1中相應的D-H參數。結合UR5機器人的D-H參數，將齊次變換矩陣A1—A6連乘得到UR5機器人從基座到末端工具的齊次變換矩陣T6：T6=A1A2A3A4A5A6=nxoxaxpx

上述式中：si表示sin θi，ci表示cos θi ，s23表示sin（θ2+θ3），c23表示cos（θ2+θ3），s234表示sin（θ2+θ3+θ4），c234表示cos（θ2+θ3+θ4）。下文中相同符號代表相同含義。

2UR5機器人逆向運動學

UR5作為一款全關節可360°旋轉的新型人機協作機器人，其肩部、肘部與第1腕關節3個相鄰關節互相平行，滿足機器人機構學中的Pieper準則[13]，其運動學逆解具有封閉解[14]。根據運動學正解的結果，采用解析法[15]中的分離變量法[16]進行運動學逆解的求取。

將UR5機器人齊次變換矩陣T6左乘矩陣A-11，右乘矩陣A-16可得：A-11T6A-16=c1s100

（1）式（1）左右兩側的第3行第4列元素相等，可得：s1（px-d6ax）-c1（py-d6ay）=d4。（2）對式（2）進行三角函數運算，可得：θ1=arctanpy-d6aypx-d6ax±arccosd4r。（3）式中r的表達式為r=（px-d6ax）2+（py-d6ay）2。（4）將UR5機器人齊次變換矩陣T6左乘矩陣A-11，可得：A-11T6=c1s100

（5）由式（5）兩側的第3行第4列元素相等可得：s1px-c1py=d6c5+d4。（6）對式（6）進行化簡可得：θ5=±arccoss1px-c1py-d4d6。（7）由式（5）中左右兩側的第3行第1列與第3行第2列相等可得：s1nx-c1ny=-s6s5， （8）

-s1 ox+c1oy=c6s5。（9）聯立式（8）和式（9）可得：θ6=±arccos-s1ox+c1oys1nx-c1ny。（10）由式（1）左右兩側第1行第3列與第2行第3列相等可得：-（c1ax+s1ay）=s5c234，（11）

az=-s5s234。（12）聯立式（11）與式（12）可得：θ234=arccosazc1ax+s1ay。（13）由式（5）的第1行第4列與第2行第4列相等可得：-d6（c1ax+s1ay）+c1px+s1py=a2c2+a3c23+d5s234，（14）

-d6az+pz-d1=a2s2+a3s23-d5c234。（15）聯立式（14）與式（15），消除變量θ23（即θ2+θ3）可得：（m1-a2c2）2+（m2-a2s2）2=a23。（16）式（16）中m1與m2分別為m1=-d6（c1ax+s1ay）+c1px+s1py-d5s234，（17）

m2=-d6az+pz+d5c234-d1 ?， ??????????????????????（18）整理可得：θ2=arccosm21+m22+a22-a23（2×a2×m1）2+（2×a2×m2）2+arctanm2m1。（19）聯立式（14）與式（15）可得：θ23=arctan-d6az+pz-d1+d5c234+a3s2-d6（c1ax+s1ay）+c1py+s1px-d5s234+a3s2。（20）聯立式（13）與式（20）可得：θ4=θ234-θ23 ??。 ?????????????????????????????（21）聯立式（19）與式（20）可得：θ3=θ23-θ2。（22）至此，UR5機器人的6個關節轉角全部求出。

3UR5奇異性分析

奇異位形是機器人機構學中重要的運動學特性[17-18]。當機器人處于奇異位形時，末端執行器的位移或旋轉運動受到限制。此時，機器人一般實際可操作自由度會減少，末端執行器不能實現某些方向的運動，也會出現某些關節角速度趨于無窮，導致機械手運動失控，機器人不能實現預定的動作[19]。由于奇異位形會嚴重影響機器人運動的穩定性，所以奇異位形分析對機器人平穩安全運動具有重要意義[20]。

雅克比矩陣反映單個關節微分運動與機器人整體微分運動之間的關系，它是判斷機器人奇異位形的重要依據，通過分析機器人處于奇異位形時的雅克比矩陣，可以得到奇異位形的約束條件，并實現對機器人的平穩控制。機器人雅克比矩陣的求解方法有矢量積法[21]、微分變換法[20]和螺旋運動求解法[22]。這里采用微分變換法求解雅克比矩陣。

進行雅克比矩陣運算時，如果關節i是轉動關節，則雅克比矩陣J的第i列按式（23）計算。

若關節i是移動關節，則雅克比矩陣J的第i列按式（24）計算：TJi=[nzozaz000]T。（24）式（23）與式（24）中的n，o，a，p分別代表inT的4個列向量，inT的計算如下所示：1nT=A1A2…An，2nT=A2A3…An，3nT=A3A4…An，…，nnT=An。UR5機器人的6個關節全為轉動關節，依據式（22）計算雅克比矩陣的各個列向量如下：TJ1=pxny-pynx

依據以上雅克比矩陣各個列元素，可得：TJ=[TJ1TJ2TJ3TJ4TJ5TJ6]。機器人機構處于奇異位形時，雅克比行列式等于零，據此條件可得：-a2s5（-a3s3+d5c34）（-a3c23-d5s234-a2c2）。令上式為零，可得3種奇異位形：-a3s3+d5c34=0，-a3c23-d5s234-a2c2=0和s5=0。

由等式-a3s3+d5c34=0可知，該奇異位形與關節3、關節4有關。通過仿真，關節3與關節4的關系如圖2所示;由等式-a3c23-d5s234-a2c2=0可知，該奇異位形與關節2—關節4有關，并得到當等式-a3c23-d5s234-a2c2=0時，關節2—關節4的關系如圖3所示;由等式s5=0可知，關節5的角度為0或180°時，機器人機構處于奇異點，此時關節4與關節6共面，如圖4所示。

4實驗驗證與工程應用

依據D-H法建立機器人坐標系后，經過理論分析與計算，最終完成機器人正向運動學與逆向運動學的解析表達式求解，并以此為基礎完成了機器人正逆向運動學控制程序的編寫，同時采用實際的UR5機器人系統進行實驗驗證。

4.1正向運動學驗證

已知機器人關節角度，利用編寫的程序運算出相應的位姿矩陣，并根據機器人系統數據加以驗證，兩組測試點測試如下。

1）設定關節角度：[90.00°，-90.00°，45.00°，-90.00°，45.00°，45.00°]，運動學計算位姿矩陣：n=[0.50，0.15，-0.85，0]，o=[-0.50，0.85，-0.15，0]，a=[0.71，0.50，0.50，0]，p=[167.45，-302.94，899.64，1]。UR5機器人系統面板數據如圖5所示，機器人實際位置p=[167.34，-303.14，899.60]，左上角圖形表示機器人實際形態，x，y，z表示機器人末端執行器的實際位置，下部為各個關節角度。

2）設定關節角度：[45.00°，-30.00°，-60.00°，-45.00°，60.00°，30.00°]，運動學計算位姿矩陣：n=[056，-0.50，-0.66，0]，o=[0.25，0.86，-0.44，0]，a=[0.79，0.08，0.61，0]，p=[-165.45，-378.36，811.22，1]。UR5機器人系統面板數據如圖6所示，機器人實際位置p=[-165.67，-378.24，811.23]，左上角位置圖形表示機器人實際形態，x，y，z表示機器人末端執行器的實際位置，下部為各個關節角度。

圖5測試點1系統面板數據

Fig.5Test point 1 system panel data圖6測試點2系統面板數據

Fig.6Test point 2 system panel data

通過PC機與機器人系統通信，讀取系統內部有關機器人末端執行器的x，y，z值與關節角度信息，結果如表2、表3所示。工控機作為上位機，基于TCP/IP協議端口完成機器人通信建立，通過30003實時反饋端口按照腳本語言的格式編寫程序發送給控制器，UR5工業機器人將反饋信息數據包發送至工控機端口，2個測試點的數據分別如圖7和圖8所示。

考慮機器人結構尺寸、位姿矩陣數據取舍以及機器人系統對數據取舍帶來的誤差，面板、機器人系統以及正向運動學程序計算得出的3組數據基本一致，從而驗證了正向運動學解法的正確性。

4.2逆向運動學驗證

利用運動學正解中隨機關節角度計算出的位姿矩陣，通過逆向運動學求解所有可能的逆解，若逆解中有相應的關節角度，即可驗證逆向運動學的正確性。

1）由測試點（1）的位姿矩陣，求得所有逆解θi

第1組：[9000°，-9000°，4500°，-9000°，4500°，4500°];第2組：[9000°，-4690°，-4500°，-4308°，4500°，4500°];第3組： [9000°，-6381°，0°，10881°，-4500°，-13500°];第4組：[-5476°，-11971°，0°，2976°，15000°，17032°];第5組：[-5476°，-11589°，16519°，-17058°，-15000°，-968°];第6組：[-5476°，-10005°，-16519°，-15339°，-15000°，-968°]。UR5機器人理論上有8組逆解，本組測試點的所有逆解中有兩組解是重復的，去掉后剩余6組解，其中第1組解與機器人實際關節角度一致。

2）由測試點（2）的位姿矩陣，求得所有逆解θi

第1組：[4500°，-8733°，6000°，-10767°，6000°，3000°];第2組：[4500°，-3000°，-6000°，-4500°，6000°，3000°];第3組：[4500°，-5579°，0°，10079°，-6000°，-15000°];第4組：[-10679°，-12608°，0°，6243°，13689°，-17928°];第5組：[-10679°，-14603°，5637°，-15399°，-13689°，072°];第6組：[-10679°，-9214°，-5637°，-9513°，-13689°，072°]。去除兩組重復解，剩余6組解，可見第2組解與機器人實際關節角度一致。

4.3工程應用驗證

在對正向運動學與逆向運動學進行實驗驗證時，限于篇幅，僅選用了兩組測試點，從驗證結果來看，可以確定正逆向運動學解析式的正確性。根據本文UR5機器人運動學算法編制的MATLAB程序在采用UR5為貼標機器人的自動貼標系統中進行了應用，經過工程示范應用檢驗，能夠實現對UR5機器人運動的控制，證明了本文UR5機器人運動學分析的正確性。

5結語

通過分析現有用戶建立的UR5機器人坐標系的不足，在UR5機器人結構特點的基礎上，采用第2種連桿坐標系建立方式初步建立機器人連桿坐標系，并根據實際的UR5機器人系統數據對所建立的坐標系進行調整，最終建立了與廠家數據匹配的UR5機器人坐標系。利用與廠家數據匹配的UR5運動學方程編寫的程序實現了與機器人系統的相互調用，解決了因坐標系不一致造成用戶無法直接利用機器人系統數據進行軌跡規劃等工程應用問題。通過微分法，在運動學的基礎上求取了UR5機器人的雅克比矩陣，并通過化簡行列式得到了UR5機器人奇異位形的數學表達式并進行了奇異位形的仿真。本文完成了UR5機器人運動學與奇異位形的理論分析以及MATLAB程序的開發，但還未能依據奇異位形的仿真結果有效避免機器人奇異位形，實現對UR5機器人連續軌跡規劃的運動控制，這也是進一步開展UR5機器人連續軌跡規劃研究需要克服的問題。

參考文獻/References：

[1]譚民， 王碩. 機器人技術研究進展[J]. 自動化學報， 2013， 39（7）： 963-972.

TAN Min， WANG Shuo. Research progress on robotics [J]. Acta Automatica Sinica， 2013， 39（7）： 963-972.

[2]駱敏舟， 方健， 趙江海. 工業機器人的技術發展及其應用[J]. 機械制造與自動化， 2015， 44（1）： 1-4.

LUO Minzhou， FANG Jian， ZHAO Jianghai. The development and the application of the industrial robot technology[J]. Machine Building & Automation， 2015， 44（1）： 1-4.

[3]計時鳴， 黃希歡. 工業機器人技術的發展與應用綜述[J]. 機電工程， 2015， 32（1）： 1-13.

JI Shiming， HUANG Xihuan. Review of development and application of industrial robot technology [J]. Journal of Mechanical & Electrical Engineering， 2015， 32（1）： 1-13.

ZHANG Fuxiang， SHI Wenjun. Inverse kinematics solver of a 2-arm hydraulic drill carriage [J]. Machinery Design & Manufacture， 2015（8）： 147-149.

[17]CRAIG J J.機器人學導論[M]. 贠超，等譯. 北京： 機械工業出版社，2013.

[18]于靖軍， 劉辛軍， 丁希侖， 等. 機器人機構學的數學基礎[M]. 北京： 機械工業出版社，2008.

[19]胡準慶， 房海容， 彭俊斌，等. 機器人奇異性分析[J]. 機器人技術與應用， 2001（6）： 32-35.

HU Zhunqing， FANG Hairong， PENG Junbin， et al. Robot singularity analysis [J]. Robot Technique and Application， 2001（6）： 32-35.

[20]呂永軍. 六關節串聯機器人機構奇異位形研究[D]. 沈陽：中國科學院研究生院（沈陽計算技術研究所）， 2016.

LYU Yongjun. Research on Singularity of 6-Joint Series Robot Mechanism [D]. Shenyang： University of Chinese Academy of Sciences （Shenyang Institute of Computing Technology） ，2016.

[21]劉蕾， 曾輝， 柳賀， 等. 六自由度機器人S型曲線速度規劃[J]. 計算技術與自動化， 2015， 34（2）： 42-45.

LIU Lei， ZENG Hui， LIU He， et al. S-curve velocity planning for 6-dof robot [J]. Computing Technique and Automation， 2015， 34（2）： 42-45.

[22]MAHONEY A W A， BBOTT J J. Generating rotating magnetic fields with a single permanent magnet for propulsion of unte-thered magnetic devices in a lumen [J]. IEEE Trans Robot， 2014， 30（2）： 411-420. 第40卷第1期河北科技大學學報Vol.40，No.1

2019年2月Journal of Hebei University of Science and TechnologyFeb. 2019