同分布強化學習優化多決策樹及其在非平衡數據集中的應用

焦江麗，張雪英，李鳳蓮，牛壯

?

同分布強化學習優化多決策樹及其在非平衡數據集中的應用

焦江麗，張雪英，李鳳蓮，牛壯

(太原理工大學 信息與計算機學院，山西 太原，030024)

針對傳統決策樹在非平衡數據集分類時少數類預測性能出現偏差的問題，提出一種基于強化學習累積回報的屬性優化策略即改進型同分布多決策樹方法。首先通過同分布隨機抽樣法對非平衡數據集中的多數類樣本進行隨機采樣，進而對各子集建立單決策樹形成多個決策樹，各決策樹采用分類回歸樹算法建樹，并利用強化學習累積回報機制進行屬性選擇策略的優化。研究結果表明：提出的基于強化學習累積回報機制的屬性優化策略可有效提高少數類被正確分類的概率；同分布多決策樹方法可有效提高非平衡數據集整體預測性能，且正類率和負類率的幾何平均值都有所提高。

非平衡數據集；多決策樹；累積回報機制屬性選擇策略；同分布隨機抽樣；強化學習

分類是數據挖掘領域的研究熱點之一，目前成熟的算法主要包括樸素貝葉斯、神經網絡和決策樹[1]等。其中，隨機森林算法因其具有簡單易行、運算速度快和準確度高的特點而在交通、醫學、生物學等眾多領域得到了廣泛應用[2?3]。然而，隨著大數據時代的到來，數據的非平衡特性也更加突出。決策樹分類算法基本思想是通過一個樹形結構模型，將數據集在不同分裂節點根據不同屬性劃分為各類別，其模型構建的核心是對分類節點的分裂屬性進行最佳選擇。其中比較經典的算法有ID3，C4.5和分類回歸樹(CART)算法 等[4?5]，這些算法的本質區別是節點分裂屬性選擇策略不同；而隨機森林方法是一種將多個單決策樹分類器集成的多決策樹學習方法[6]，在一定程度上可以解決單決策樹過擬合導致的分類準確性不高的問題。上述單決策樹方法及隨機森林方法用于平衡數據集，一般可得到較好的分類效果，但對非平衡數據集，這些方法則存在少數類預測準確度偏低的缺陷。為此，人們提出多種改進算法。ALSHOMRANI等[7]利用特征加權法優化屬性選擇策略以改善非平衡數據集分類性能。在對非平衡數據集進行分類時，由于各類別的樣本數目分布不均勻，少數類樣本通常得不到充分訓練，從而使分類器容易傾向于多數類而忽略少數類樣本，但在現實生活中少數類樣本通常具有更重要的作 用[8?9]，因此，如何提高少數類預測準確度具有重要意義。目前，國內外研究者針對非平衡數據集如何提高分類器性能開展了大量工作：LI等[10]提出了基于屬性混合策略的代價敏感Top-N多決策樹算法，并將其用于非平衡數據集分類預測；KOZIARSKI等[11]提出了一種用于改變非平衡數據集數據不平衡率的預處理方法；付忠良[12]提出了一種多標簽代價敏感分類集成學習算法。但針對非平衡數據分類問題，雖然引入代價敏感因子和采用抽樣的方法可提高分類的性能，但在實施中往往難以確定代價，且抽樣的方法容易造成樣本信息丟失或者過擬合等問題。強化學習方法是從自適應控制理論中發展出來的一種機器學習方法，其通過判斷當前學習環境對分類器的影響，綜合分析各種影響所造成的結果可對學習方法進行調整，從而使最終的分類預測偏向更加準確的結果[13?14]。周浦城等[15]將Q-Learning強化學習算法與決策樹模型相結合，根據決策樹當前節點輸入的數據不斷更新Q?表生成新的決策節點。人們對利用強化學習方法進行屬性選擇策略優化的研究較少，而屬性選擇直接影響決策樹性能，為此，本文作者首先基于強化學習累積回報機制提出一種屬性選擇優化策略，進而將該策略與集成學習算法結合，提出一種基于同分布隨機抽樣的多決策樹集成學習算法。

1 基于強化學習累積回報機制的優化策略

強化學習是研究一個能夠感知環境的智能體，在沒有先驗知識的情況下，從延遲回報中學習優化的控制策略，進而使智能體的累積回報最大[16]。傳統決策樹采用特征選擇策略建樹以實現分類，其中CART算法采用基尼(Gini)指數作為特征選擇策略，對非平衡數據集分類時會使多數類數據分類性能更優[17]。由于強化學習會根據智能體做出動作后的執行結果進行獎勵或者懲罰，并通過延遲回報獲得各個狀態下的最優動作。若能借鑒這種獎懲策略，使少數類分類正確時獲得更大的獎勵，并將這種策略融合于決策樹屬性選擇階段，則有利于提高決策樹中少數類分類性能。借鑒這種優化思路，本文作者提出基于累積回報機制的屬性選擇優化策略，通過決策樹每一層的回報系數計算決策樹屬性選擇的累積回報值以使決策樹屬性選擇策略得到優化。

1.1 累積回報求解

依據強化學習的累積回報思想，結合CART算法，通過每一層的回報系數優化決策樹的屬性選擇策略，本文將第1~層的層累積回報系數相乘定義為累積回報，其具體表達式如下：

=1?2…R(1)

式中：R為該節點在決策樹的第層的累積回報系數，R越大，說明分類性能越優。考慮預測效果的幾何平均值系數、真實正類率以及模型的準確率，本文將R定義為

R=+i?A?mi(2)

式中：P為分類模型第層的真實正類率即正確預測的正類與實際為正類的樣本數量的比值，+i越大，說明正類預測越準確，性能越好；A為模型第層分類準確率即正確預測的樣本數與總樣本數的比值，其值越大，說明總體預測越準確，性能越好；mi為模型中第層幾何平均值系數即真實正類率與真實負類率乘積的開方，其值越大，說明總體預測性能越好。

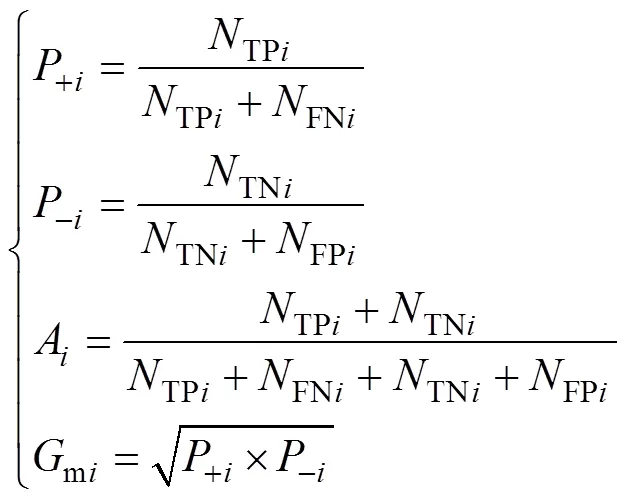
式中：?i為分類模型中第層的真實負類率即正確預測的負類與實際為負類的樣本數量的比值，其值越大，說明負類預測越準確，性能越好；TPi為所有樣本在當前節點第層被正確的分為正類的數量；TNi為所有樣本在當前節點第層正確分為負類的數量；FPi為第層錯誤分為正類的樣本數量，FNi為第層錯誤分為負類的樣本數量。

1.2 基于累積回報機制的屬性選擇策略

傳統的屬性選擇策略在非平衡數據集預測中表現并不佳[18?19]，為此，本文作者結合上述強化學習累積回報機制的思想，提出基于強化學習的累積回報機制的屬性選擇策略(cumulative reward mechanism attributes selection strategy, CRS)，利用每個屬性被選擇后當前節點的分類結果作為影響因子反饋到當前節點屬性選擇的過程中，即在傳統屬性選擇方法的基礎上加入累積回報系數進行當前節點最佳分裂屬性選擇的優化。屬性選擇策略AS定義為

式中：Gini為所有屬性的Gini系數。在傳統決策樹屬性選擇中，Gini系數越小，最終分類效果越好，而累積回報系數R越大，說明對屬性選擇的優化效果越好，因此，選擇AS最小值對應的屬性作為當前節點分裂的屬性最好。

1.3 基于累積回報機制的決策樹模型構建

本文采用自上向下遞歸二分技術，利用強化學習累積回報機制得到各節點的最佳分裂屬性。基于累積回報機制的決策樹(cumulative reward mechanism attributes selection strategy decision tree, CRDT)原理圖如圖1所示。

圖1中CART決策樹根節點采用傳統的屬性選擇策略構建，各子節點的構建采用本文提出的累積回報機制，即根據式(4)計算各子節點的AS，最小AS對應的屬性為子節點最佳屬性，直至達到葉節點。

圖1 CRDT原理圖

2 同分布隨機抽樣的CRS多決策樹集成學習算法

在數據集不平衡的情況下，少數類被抽取的概率很小，而經典隨機森林中單決策樹的訓練樣本是隨機抽取的，因此，少數類在最后決策樹形成過程中不會被充分訓練[20]。已有方法是將非平衡數據集中的多數類樣本隨機分為個子集，然后，分別將這些子集中的樣本與少數類樣本合成新的訓練樣本子集，通過個決策樹對各個新的樣本子集分別進行訓練，最后采用投票法將這些決策樹結果集成。但此種方法使個數據集之間的多數類樣本完全不同，雖然少數類樣本得到了充分訓練，但多數類樣本訓練不足，因此，這種方法的分類效果并不理想。

為此，本文作者提出一種同分布隨機抽樣的CRS多決策樹集成學習(identically distributed random sampling cumulative reward attributes selection strategy multi-decision tree, IDCRMDT)算法。該方法首先對輸入數據集采用同分布隨機抽樣法進行預處理，得到個樣本子集，以使非平衡數據集中的多數類樣本均勻分布至各子集，進而使用本文提出的累積回報屬性選擇策略建立各個單決策樹。IDCRMDT算法原理圖如圖2所示。

圖2中同分布隨機抽樣法使用-means聚類算法對輸入數據集中的多數類進行聚類，得到各決策樹訓練時使用的樣本子集，這樣既可以保證抽取的多數類樣本服從同分布，又可以使少數類樣本也被均勻抽樣，克服了非平衡數據集的非平衡率過大時少數類樣本得不到充分訓練的弊端。

2.1 同分布隨機抽樣法

本文提出的IDCRMDT算法首先采用同分布隨機抽樣法對多數類樣本進行聚類，形成(選取和少數類樣本一致的個數)個樣本子集ma，以使分布相近的多數類樣本劃分為1個集合，然后將各個子集分別與少數類樣本進行組合形成新的同分布樣本子集。同分布隨機抽樣法流程圖如圖3所示。

2.2 IDCRMDT算法

數據樣本集合分為多數類樣本集合ma和少數類樣本集合mi，記多數類樣本的數量為，少數類樣本的數量為。IDCRMDT算法流程如下。

輸入：數據集。

圖2 IDCRMDT算法原理圖

圖3 同分布隨機抽樣法流程圖

輸出：分類預測結果。

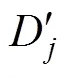
3) 使用投票法得到多決策樹分類預測結果。

3 實驗及結果分析

本文設計實驗分別驗證基于強化學習累積回報的屬性選擇策略的優勢以及提出的IDCRMDT算法性能優劣。

3.1 實驗數據

實驗數據集采用KEEL-Imbalanced Data Sets中的10個不同平衡率的非平衡數據集，各數據集詳情如表1所示。

3.2 實驗設計

本文設計實驗方案，并采用10折交叉驗證的方法得到實驗結果。

1) 方案1。

對比方法：CART(單決策樹)；

表1 實驗數據集

本文方法：CRDT(基于累積回報機制的單決策樹)。

2) 方案2。

對比方法1：RF(傳統隨機森林算法)；

對比方法2：CRRF(基于單決策樹CRS屬性選擇策略的隨機森林，cumulative reward mechanism attributes selection strategy random forest)；

本文方法：IDCRMDT(同分布隨機抽樣的CRS多決策樹)。

3.3 評價指標

本論文采用真實正類率+、準確率和幾何平均值m評估算法的性能。其中，真實正類率P和準確率越大，說明決策樹的分類效果更好，而幾何平均值m是真實正類率和真實負類率乘積的開方，對于非平衡數據集而言更能反映總體預測分類性能的 優劣。

3.4 實驗結果

本文提出的方法CRDT與CART單決策樹性能對比見圖4。由圖4(a)可知：相較CART，采用本文提出的CRDT算法各數據集的真實正類率+均有所提高；對于數據集3，4，7，9和10，真實正類率分別提高16.7%，9.9%，22.0%，27.7%和60.2%。由圖4(b)可以看出：除數據集1外，采用CRDT各數據集的準確率均有所提高。由圖4(c)可以看出：除了數據集1之外，采用CRDT時其余數據集幾何平均值m都有所提高。綜合來看，CRDT應用于非平衡數據集整體性能比已有的CART算法的分類性能更優。

將傳統的隨機森林算法(RF)與本文提出的IDCRMDT和CRRF的真實正類率、準確率以及幾何平均值進行對比，結果如圖5所示。從圖5(a)和圖5(b)可知：采用本文的IDCRMDT算法時，除數據集10的真實正類率下降較多外，其余數據集的真實正類率都比采用RF和CRRF時的真實正類率高，但準確率提高幅度不是很明顯。由圖5(c)可知：采用本文的IDCRMDT算法時，數據集1，2，3，5和8的m與采用傳統隨機森林算法(RF)得到的m相比均有所提高，而較CRRF得到的m則分別提高3.9%，16.9%，6.3%，7.8%和32.2%。

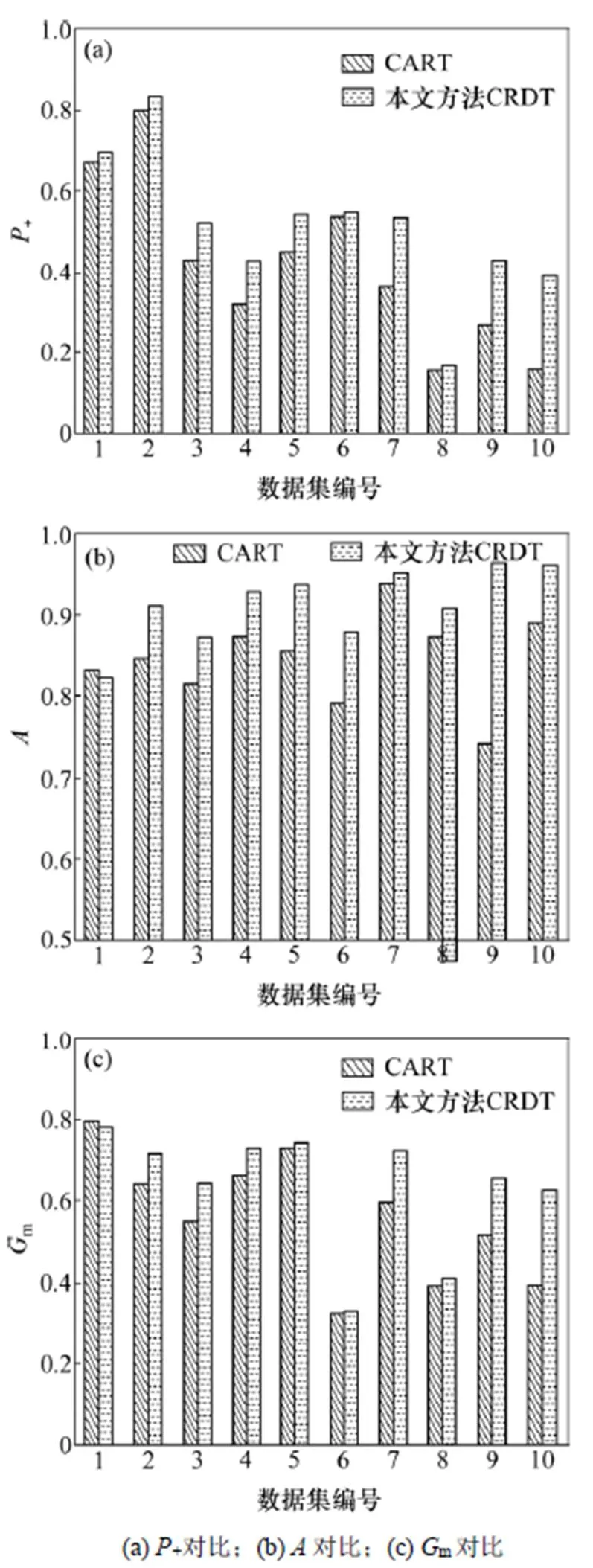
圖4 CRDT與CART性能對比

圖5 IDCRMDT與CRRF和RF的性能對比

從實驗方案1可以看出：利用強化學習累積回報機制思路改進決策樹屬性選擇策略的性能都有所提高。隨機森林算法在很大程度上解決了單決策樹的過擬合問題，傳統的隨機森林在建樹過程中采用可放回隨機抽樣方法產生不同的數據集，但往往非平衡數據集的少數類被抽取的概率會很小。從實驗方案2可以看出：采用同分布隨機抽樣的方法可使少數類得到充分訓練，與傳統的RF以及改進的屬性選擇策略的CRRF算法相比，本文提出的IDCRMDT算法的真實正類率和準確率均有所提高，同時，模型整體性能有所提高。

4 結論

1) 本文提出一種同分布類隨機抽樣的CRS多決策樹集成學習(IDCRMDT)算法，利用累積回報機制進行決策樹屬性選擇優化，并對非平衡數據集中的多數類采用同分布隨機抽樣法進行預處理，以使多數類樣本均勻分布于各子集并使少數類樣本得到充分訓練。

2) 本文提出的方法對多數非平衡數據集的分類效果均有提升；而對于個別數據集，雖然少數類分類性能得到了提高，但數據集整體預測性能稍有下降。

[1] HAN Jiawei, KAMBER M, PEI Jian. Data mining: concepts and techniques[M]. 3rd ed. San Francisco, USA: Elsevier, 2011: 15?23.

[2] 楊宏宇, 徐晉. 基于改進隨機森林算法的Android惡意軟件檢測[J]. 通信學報, 2017, 38(4): 8?16. YANG Hongyu, XU Jin. Android malware detection based on improved random forest[J]. Journal on Communications, 2017, 38(4): 8?16.

[3] 杜春蕾, 張雪英, 李鳳蓮. 改進的CART算法在煤層底板突水預測中的應用[J]. 工礦自動化, 2014, 40(12): 52?56. DU Chunlei, ZHANG Xueying, LI Fenglian. Application of improved CART algorithm in prediction of water inrush from coal seam floor[J]. Industry and Mine Automation, 2014, 40(12): 52?56.

[4] STROBL C. Fifty years of classification and regression trees discussion[J]. International Statistical Review, 2014, 82(3): 349?352.

[5] 姚亞夫, 邢留濤. 決策樹C4.5連續屬性分割閾值算法改進及其應用[J]. 中南大學學報(自然科學版), 2011, 42(12): 3772? 3776. YAO Yafu, Xing Liutao. Improvement of C4.5 decision tree continuous attributes segmentation threshold algorithm and its application[J]. Journal of Central South University (Science and Technology), 2011, 42(12): 3772?3776.

[6] 鄧生雄, 雒江濤, 劉勇, 等. 集成隨機森林的分類模型[J]. 計算機應用研究, 2015, 32(6): 1621?1624. DENG Shengxiong, LUO Jiangtao, LIU Yong, et al. Classification model based on ensemble random forests[J]. Application Research of Computers, 2015, 32(6): 1621?1624.

[7] ALSHOMRANI S, BAWAKID A, SHIM S O, et al. A proposal for evolutionary fuzzy systems using feature weighting: dealing with overlapping in imbalanced datasets[J]. Knowledge-Based Systems, 2015, 73(1): 1?17.

[8] BEYAN C, FISHER R. Classifying imbalanced data sets using similarity based hierarchical decomposition[J]. Pattern Recognition, 2015, 48(5): 1653?1672.

[9] 陳橙, 顏艷, 何瓊, 等. 決策樹與logistic回歸模型用于開奶時間延遲影響因素分析[J]. 中南大學學報(醫學版), 2018, 43(3): 306?312. CHEN Cheng, YAN Yan, HE Qiong, et al. Risk factors for delayed breastfeeding initiation based on decision tree model and logistic regression model[J]. Journal of Central South University (Medical Sciences), 2018, 43(3): 306?312.

[10] LI Fenglian, ZHANG Xueying, ZHANG Xiqian, et al. Cost-sensitive and hybrid-attribute measure multi-decision tree over imbalanced data sets[J]. Information Sciences, 2018, 422: 242?256.

[11] KOZIARSKI M, WO?NIAK M. CCR: A combined cleaning and resampling algorithm for imbalanced data classification[J]. International Journal of Applied Mathematics & Computer Science, 2017, 27(4): 727?736.

[12] 付忠良. 多標簽代價敏感分類集成學習算法[J]. 自動化學報, 2014, 40(6): 1075?1085. FU Zhongliang. Cost-sensitive ensemble learning algorithm for multi-label classification problems[J]. Acta Automatica Sinica, 2014, 40(6): 1075?1085.

[13] LI Hongjia, CAI Ruizhe, LIU Ning et al. Deep reinforcement learning: Algorithm, applications, and ultra-low-power implementation[J]. Nano Communication Networks, 2018, 16: 81?90.

[14] WU Jingda, HE Hongwei, PENG Jiankun, et al. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus[J]. Applied Energy, 2018, 222: 799?811.

[15] 周浦城, 洪炳镕. 基于決策樹的強化學習算法[J]. 計算研究與發展, 2005, 42(S): 233?237. ZHOU Pucheng, HONG Bingrong. Decision tree based reinforcement learning algorithm[J]. Journal of Computer Research and Development, 2005, 42(S): 233?237.

[16] SUTTON R S, BARTO A G. Reinforcement learning: an introduction[M]. 2nd ed. London, UK: MIT Press, 2018: 1?68

[17] SUN Shasha, FAN Wenlai, XU Yan, et al. Comparative analysis of the aroma components of Cabernet Sauvignon in four regions [J]. Science & Technology of Food Industry, 2013, 34(24): 70?69.

[18] ALSHOMRANI S, BAWAKID A, SHIM S O, et al. A proposal for evolutionary fuzzy systems using feature weighting: Dealing with overlapping in imbalanced datasets[J]. Knowledge-Based Systems, 2015, 73(1): 1?17.

[19] ANTONELLI M, DUCANGE P, MARCELLONI F. An experimental study on evolutionary fuzzy classifiers designed for managing imbalanced datasets[J]. Neurocomputing, 2014, 146: 125?136.

[20] ARCHER K J, KIMES R V. Empirical characterization of random forest variable importance measures[J]. Computational Statistics and Data Analysis, 2008, 52(4): 2249?2260.

Identically distributed multi-decision tree based on reinforcement learning and its application in imbalanced data sets

JIAO Jiangli, ZHANG Xueying, LI Fenglian, NIU Zhuang

(College of Information and Computer, Taiyuan University of Technology, Taiyuan 030024, China)

As the general decision tree can not classify the minority class of the imbalanced data sets well, an improved identically distributed multi-decision tree approach based on reinforcement learning cumulative reward was proposed to optimize the attribute selection strategy. Firstly, the majority class samples of the imbalanced data sets were randomly sampled by the identically distributed random sampling approach, and then each single decision tree was established over each subset and eventually a multi-decision tree was formed. Each single decision tree was constructed by classification and regression tree(CART) algorithm firstly and then reinforcement learning cumulative reward mechanism was utilized to optimize the attribute selection strategy. The results show that the proposed attribute optimization strategy based on the reinforcement learning cumulative reward mechanism effectively improves the probability that the minority class can be correctly classified. The identically distributed multi-decision tree method effectively improves the overall prediction performance over imbalanced data sets. Moreover, the positive rate and geometric mean value of positive and negative rates are improved at the same time.

imbalanced data sets; multi-decision tree; cumulative reward mechanism attributes selection strategy; identically distributed random sampling; reinforcement learning

TP301

A

1672?7207(2019)05?1112?07

10.11817/j.issn.1672?7207.2019.05.014

2018?06?11；

2018?08?11

國家自然科學基金資助項目(61376693)；山西省重點研發計劃(社會發展領域)項目(201803D31045)；山西省自然科學基金資助項目(201801D121138)；山西省重大專項(20181102008)；山西省優秀人才科技創新項目(201605D211021) (Project(61376693) supported by the National Natural Science Foundation of China; Project(201803D31045) supported by Key R&D (Social Development) Program of Shanxi Province;Project(201801D121138) supported by the Natural Science Foundation of Shanxi Province; Project(20181102008) supported by the Major Program of Shanxi Province; Project(201605D211021) supported by the Science and Technology Innovation Program for Excellent Talents in Shanxi Province)

張雪英，博士，教授，博士生導師，從事語音信號處理以及人工智能等研究；E-mail: tyzhangxy@163.com

(編輯 伍錦花)