高應力泥質(zhì)粉砂巖黏彈塑性蠕變模型

劉新喜，李盛南，徐澤佩，李玉，高學文，王瑋瑋

?

高應力泥質(zhì)粉砂巖黏彈塑性蠕變模型

劉新喜1,2，李盛南1,2，徐澤佩1,2，李玉1,2，高學文1，王瑋瑋1

(1. 長沙理工大學 土木工程學院，湖南 長沙，410114；2. 橋梁結(jié)構(gòu)安全控制湖南省工程實驗室，湖南 長沙，410114)

為揭示高應力作用下深埋硐室圍巖的流變特性，采用分級增量加載方式對泥質(zhì)粉砂巖進行三軸壓縮蠕變實驗，根據(jù)穩(wěn)態(tài)蠕變速率與應力的關(guān)系，利用給定蠕變速率閾值確定巖石的長期強度；結(jié)合蠕變曲線特征，將瞬彈性、黏彈性、黏塑性應變分離，建立模型各參數(shù)與應力和時間的函數(shù)關(guān)系；根據(jù)損傷定義確定瞬彈性、黏彈性元件的損傷變量，并引入瞬彈性、黏彈性損傷變量和黏塑性修正系數(shù)對西原模型進行優(yōu)化，提出一種可以描述高應力作用下巖石蠕變?nèi)^程的變參數(shù)模型。研究結(jié)果表明：穩(wěn)態(tài)蠕變速率隨應力增大呈指數(shù)增大，采用給定蠕變速率閾值求得巖石的長期強度為68.82 MPa，為單軸抗壓強度的74.80%；基于黏彈塑性應變分離建立的蠕變模型能夠很好地描述巖石蠕變?nèi)^程的非線性特征，且優(yōu)化模型與實驗數(shù)據(jù)擬合較好，證明了該蠕變模型的合理性。

巖石力學；泥質(zhì)粉砂巖；蠕變實驗；蠕變模型；非線性

在高應力作用下，深埋硐室流變破壞問題已嚴重影響我國地下工程的建設(shè)[1?2]。在深埋硐室二次襯砌施工完成后，由于襯砌剛度較大，圍巖和支護結(jié)構(gòu)處于暫時穩(wěn)定狀態(tài)。但在高地應力長期作用下，圍巖內(nèi)部結(jié)構(gòu)不斷調(diào)整重組，使得圍巖蠕變持續(xù)發(fā)展，承載能力下降，進而導致圍巖破壞和支護結(jié)構(gòu)失效[3]。研究高應力作用下巖石的蠕變特性對深埋硐室支護設(shè)計和長期穩(wěn)定性評價具有重要意義。巖石在高應力作用下的蠕變具有明顯非線特征[4?6]，而以往的研究大多基于元件理論，通過線性元件Hooke體、St.Venant體、Newton體串聯(lián)或并聯(lián)組合模型來描述巖石蠕變的彈性、黏彈性、黏塑性等特性，該方法建立的模型具有嚴格的理論意義，但模型均由線性元件組合，得到的本構(gòu)關(guān)系不能反映巖石蠕變的非線性特征[7]。近年來，許多學者在元件理論的基礎(chǔ)上，通過引入非線性元件來改進模型，使得模型在加速蠕變過程具有非線性特征，并通過數(shù)值擬合對模型參數(shù)進行識別，建立了巖石蠕變的變參數(shù)模型。如王軍保等[8]采用一種黏滯系數(shù)隨應力和時間變化的非線性黏滯元件，將之與經(jīng)典的彈性、黏性元件組合，建立了可以反映巖石蠕變非線性特征的模型。張治亮等[9]提出了能夠反映不同圍壓下巖石加速啟動時間的非線性元件，并與Burgers模型組合，建立了巖石在不同圍巖下的非線性黏彈塑性蠕變模型。高賽紅等[10]針對高應力作用下巖石蠕變的非線性特征，提出將瞬時Hooke體、瞬時塑性、村山體和非線性黏塑體組合，建立了能夠描述巖石蠕變?nèi)^程特征的非線性模型。康永剛等[11]將Burgers模型中的牛頓黏壺元件改進為與應力水平和時間相關(guān)的變量，改進的模型能描述巖石蠕變的全過程。齊亞靜等[12]針對傳統(tǒng)的西原模型難以描述巖石非線性流變特性的問題，提出了一個帶應變觸發(fā)的非線性塑性元件與西原模型串聯(lián)，改進的模型能很好地反映巖石加速蠕變的非線性特征。LI等[13]通過將Burgers模型與塑性元件串聯(lián)，提出一種能描述層狀復合巖石蠕變特性的新模型。蔣海飛等[14]在Burgers模型上串聯(lián)1個非線性黏性元件，所建立的模型能夠描述高圍壓高水壓條件下巖石的加速蠕變。趙寶云等[15]通過Kelvin體與非線性黏塑性元件串聯(lián)，提出了一種描述短時蠕變的非線性蠕變模型。上述對巖石蠕變模型非線性特征的研究大多集中在加速蠕變階段，只考慮了模型中黏滯系數(shù)隨時間和應力的變化影響，而已有研究表明高應力作用下巖石的非線性特征貫穿巖石整個蠕變過程，模型中各參數(shù)均應視為變量。對此，劉新喜等[16]在Burgers模型的基礎(chǔ)上，基于損傷理論建立了模型各參數(shù)隨時間和應力變化的損傷方程，提出了高應力作用下巖石非線性蠕變損傷模型，并具有較好的擬合效果。但模型中各參數(shù)僅通過蠕變曲線整體擬合自動識別，得到的模型參數(shù)變化規(guī)律很難客觀反映蠕變各階段彈性和塑性蠕變的真實變化規(guī)律。針對上述研究的不足，本文作者在對泥質(zhì)粉砂巖進行三軸壓縮蠕變實驗的基礎(chǔ)上，根據(jù)穩(wěn)定蠕變速率與應力的關(guān)系，采用給定蠕變速率閾值確定巖石的長期強度；結(jié)合巖石蠕變曲線特征，以長期強度為黏塑性蠕變的應力閾值，分別對瞬彈性、黏彈性、黏塑性應變進行分析，并通過數(shù)值擬合建立各個蠕變參數(shù)與應力和時間的函數(shù)關(guān)系，引入損傷方程和黏塑性修正系數(shù)對模型進行優(yōu)化，提出一種可以描述高應力作用下巖石蠕變的變參數(shù)模型，可望為深埋硐室圍巖支護設(shè)計和長期穩(wěn)定性評價提供參考。

1 蠕變實驗

1.1 試樣制備及實驗過程

在某深埋硐室施工現(xiàn)場選取新開挖的泥質(zhì)粉砂完整巖塊，利用ZS?100巖石鉆芯取樣機垂直巖塊層理進行取芯，取芯方法采用水鉆法；利用SHM?200雙端面打磨機對切割完好芯樣進行打磨，制備成直徑×高為50 mm×100 mm的圓柱體標準試件，控制徑向誤差不大于0.5 mm。制備好的試樣見圖1(a)。采用RLW?2000三軸流變實驗儀器進行三軸流變實驗，實驗裝置見圖1(b)。為模擬巖石的高地應力，設(shè)定圍壓為20 MPa。實驗加載方式為分級增量加載，根據(jù)泥質(zhì)粉砂巖單軸抗壓強度92.0 MPa，從30~100 MPa分為8級加載，應力加載速率為0.1~0.3 MPa/s，每一級加載應力持續(xù)48 h以上。當軸向應變小于0.001 d?1時，可認為巖石蠕變速率不再發(fā)生改變，即巖石處于穩(wěn)定狀態(tài)，然后進行下一級加載，直至巖石試樣被破壞 為止。

1.2 實驗結(jié)果

泥質(zhì)粉砂巖在各級應力作用下的蠕變曲線見圖2。從圖2可見：巖石蠕變曲線具有明顯非線性特征，在各級應力作用下，巖石均出現(xiàn)瞬彈應變和衰減蠕變；在較低應力(小于60 MPa)作用下，巖石蠕變速率逐漸減小，并趨近于0 h?1，巖石只出現(xiàn)衰減蠕變；在較高應力時(70~90 MPa)，巖石蠕變速率隨時間減小，最終保持穩(wěn)定，進入定常蠕變階段；當應力大于單軸抗壓強度(大于92.0 MPa時)，巖石經(jīng)歷短暫的穩(wěn)定蠕變，很快就發(fā)生加速蠕變破壞。

(a) 試驗試樣；(b) 流變試驗儀器

高應力作用下巖石的蠕變?nèi)^程曲線見圖3。由圖3可知：

應力/MPa：1—30；2—40；3—50；4—60；5—70；6—80；7—90；8—100。

圖3 高應力作用下巖石的全蠕變曲線

表1 蠕變各階段的應變

2 長期強度

長期強度是巖石進入加速蠕變的應力閾值，即為蠕變由穩(wěn)定狀態(tài)向加速狀態(tài)發(fā)展的拐點。確定巖石長期強度的方法主要有直接法和間接法。由于采用直接法需要進行大量實驗，持續(xù)時間較長，目前多采用間接法，其包括等時曲線法和過渡蠕變法等[17]。等時曲線的拐點具有多變性，該方法用于確定巖石長期強度的準確性還需進一步探討[18]；過渡蠕變法需要確定蠕變速率為零的最大荷載，在實驗過程中受實驗裝置及外界環(huán)境影響，一般很難得到[19]。采用給定蠕變速率閾值作為巖石蠕變拐點，能降低確定巖石長期強度的難度，往往能取得較好的效果。為消除衰減蠕變階段的影響，準確求得穩(wěn)態(tài)蠕變階段的蠕變速率，取各級應力蠕變20 h后的穩(wěn)態(tài)蠕變曲線進行擬合，得到各級應力作用下的穩(wěn)態(tài)蠕變速率見表2。

表2 各應力狀態(tài)下穩(wěn)態(tài)蠕變速率

穩(wěn)態(tài)蠕變速率與應力的關(guān)系曲線見圖4。各級應力作用下巖石穩(wěn)態(tài)蠕變速率并不為0 h?1，巖石穩(wěn)定蠕變速率隨應力呈指數(shù)增加；當應力小于60 MPa時，巖石的穩(wěn)態(tài)蠕變速率變化較小((5.052~19.329)× 10?8h?1)；當應力大于60 MPa時，巖石的穩(wěn)態(tài)蠕變速率迅速增大。穩(wěn)定蠕變速率與加載應力的擬合關(guān)系式為

圖4 各級應力作用下穩(wěn)定蠕變階段的蠕變速率

=5.147 2×10?8+1.078 6×10?9×exp(0.096 8)，

2=0.985 (3)

3 蠕變模型

在高應力作用下，泥質(zhì)粉砂巖蠕變具有明顯應力閾值即巖石的長期強度。當應力小于閾值時，巖石硬化效應強于損傷效應，顆粒間膠結(jié)物受外力作用產(chǎn)生的裂隙隨巖石顆粒體流動逐漸閉合；外力撤銷后，顆粒體的變形可立即恢復，顆粒間相對位移隨時間緩慢恢復，在宏觀上表現(xiàn)出巖石蠕變的瞬彈和黏彈性特征。當應力大于閾值時，巖石損傷效應強于硬化效應，在外力作用下巖石顆粒體間裂隙逐漸開展，進而導致巖石顆粒體局部破壞。當外力撤銷時，顆粒體的變形可立即恢復，而顆粒間膠結(jié)物未破壞部分隨時間逐漸恢復，破壞部分不能恢復，在宏觀上表現(xiàn)出巖石蠕變的瞬彈性、黏彈性和黏塑性特征[21?22]。結(jié)合蠕變曲線特征分析，巖石的蠕變模型可由Hooke體、Kelvin體和Bingham體組成。傳統(tǒng)的西原模型能很好描述巖石黏彈塑性特征，且能反映巖石加速蠕變時的應力閾值，其模型組成元件如圖5所示，模型方程見式(5)。

圖5 西原模型

式中：0為瞬時變形模量；ce為黏彈性變形模量；ce為黏彈性黏滯系數(shù)；dc為黏塑性黏滯系數(shù)；s為長期強度。該模型均由線性元件組成，當應力超過應力閾值時，顆粒體的膠結(jié)狀態(tài)發(fā)生破壞，顆粒體間的黏滯流動并非線性。為此，本文在西原模型的基礎(chǔ)上，以長期強度為黏塑性應變的應力閾值，將巖石蠕變的瞬彈性、黏彈性和黏塑性蠕變分離，通過數(shù)值擬合工具分別對其蠕變參數(shù)進行識別，建立瞬彈性、黏彈性和黏塑性蠕變參數(shù)與應力和時間的函數(shù)關(guān)系，并引入?yún)?shù)修正變量對西原模型進行優(yōu)化，即可得到高應力泥質(zhì)粉砂巖蠕變?nèi)^程的變參數(shù)模型。

3.1 瞬時變形模量

求得各級應力作用下巖石的瞬時變形模量見圖6。從圖6可見，巖石瞬時變形模量隨應力增加而減小。通過數(shù)值擬合得到各級應力作用的瞬時變形模量表達式：

其中：E(0,i)為第i級加載的瞬時變形模量；σi為加載 應力。

巖石是多相復合結(jié)構(gòu)材料，在成巖過程中，因長期的地質(zhì)運動，內(nèi)部存在大量的節(jié)理裂隙。由于深埋硐室圍巖長期在高應力作用下內(nèi)部裂隙被擠密壓實，當圍巖被開挖出來時，應力突然釋放使得巖石裂隙開展造成巖體損傷。進行巖石蠕變實驗時，瞬時加載過程使得巖石損傷進一步加劇。根據(jù)損傷定義可得巖石初始損傷變量(0,i)為

3.2 黏彈變形模量

當應力小于長期強度時，巖石衰減蠕變見圖7，可見巖石蠕變速率逐漸減小趨于0 h?1，蠕變主要由瞬彈性、黏彈性蠕變組成。巖石黏彈蠕變ce可由下式進行計算：

應力/ MPa：1—30；2—40；3—50；4—60。

圖7 應力小于長期強度的衰減階段應變

Fig. 7 Attenuation stage strain when stress is smaller than long-term strength

應力/ MPa：1—30；2—40；3—50；4—60。

巖石蠕變可用Kelvin體來擬合黏彈性應變，通過擬合參數(shù)見表3。

表3 黏彈性蠕變擬合參數(shù)

根據(jù)Kelvin體本構(gòu)方程

通過計算得到巖石蠕變速率見圖9。

應力/ MPa：1—30；2—40；3—50；4—60。

求得黏彈性變形模量如圖10所示。

利用最小二乘法對黏彈性變形模量進行擬合可得

各級應力巖石黏彈性變形模量的參數(shù)見表4。

巖石黏彈性變形模量擬合參數(shù)是與應力有關(guān)的參數(shù)，通過擬合得到擬合參數(shù)與應力的關(guān)系：

應力/ MPa：1—30；2—40；3—50；4—60。

表4 應力小于長期強度時黏彈性變形模量擬合參數(shù)

根據(jù)式(18)，(19)和(20)計算當應力大于長期強度時黏彈性變形模量的相關(guān)參數(shù)見表5。將表5中各參數(shù)代入式(17)即可得當應力大于長期強度時各級應力的黏彈性變形模量，見圖11。

表5 應力大于長期強度時黏彈性變形模量擬合參數(shù)

應力/ MPa：1—70；2—80；3—90；4—100。

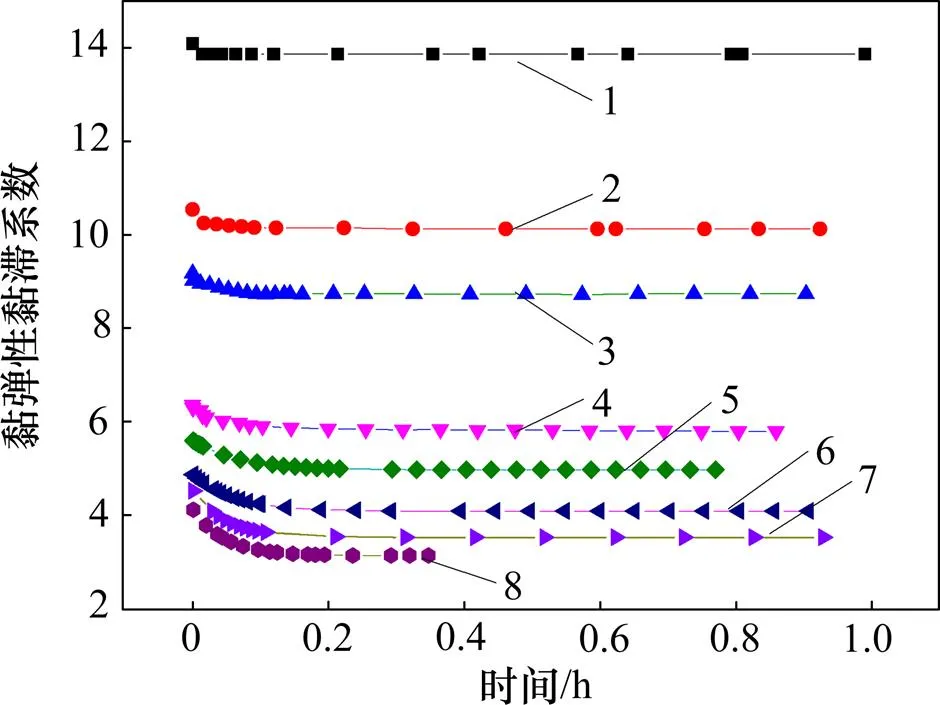
應力/ MPa：1—30；2—40；3—50；4—60；5—70；6—80；7—90；8—100。

從圖10~12可知：巖石黏彈性變形模量和黏彈性黏滯系數(shù)均隨時間增加而減小，最終趨于穩(wěn)定，應力越大，保持穩(wěn)定需要的時間越長。從巖石損傷角度看，巖石在外力作用下巖石顆粒體間產(chǎn)生細小裂隙，但隨著顆粒體定向流動，微裂隙逐漸發(fā)生閉合，使得巖石損傷得到抑制，表現(xiàn)出巖石應變速率隨時間逐漸減小；當顆粒體定向排列穩(wěn)定時，巖石應變速率趨近于0；應力越大，顆粒體硬化流動時間越長，蠕變穩(wěn)定需要的時間就越長。

根據(jù)損傷定義，巖石黏彈性變形模量損傷因子和黏彈性黏滯系數(shù)損傷因子可表示為：

巖石的黏彈性變形模量和黏彈性黏滯系數(shù)的損傷因子與時間的關(guān)系分別見圖13和圖14。

應力/ MPa：1—30；2—40；3—50；4—60；5—70；6—80；7—90；8—100。

應力/ MPa：1—30；2—40；3—50；4—60；5—70；6—80；7—90；8—100。

黏彈性變形模量和黏滯系數(shù)的損傷因子可由下式進行擬合：

3.3 黏塑性黏滯系數(shù)

表6 黏彈性變形模量和黏滯系數(shù)損傷因子擬合參數(shù)

當應力大于長期強度時，巖石顆粒體間的膠結(jié)狀態(tài)發(fā)生破壞，顆粒體定向流動并不能完全使裂隙閉合；隨著時間增加，顆粒體間的裂隙持續(xù)發(fā)展，巖石蠕變速率保持穩(wěn)定，巖石損傷不斷積累，顆粒體破壞狀態(tài)從局部向周邊發(fā)展，使得巖石黏塑性變形積累；隨著裂隙開展，巖石有效承載面積減小，最終巖石發(fā)生破壞。黏塑性變形dc可由下式進行計算：

計算得到的應力大于長期強度的黏塑性應變見圖15。

從圖15可知：在高應力作用下，巖石的黏塑性應變在整個蠕變過程均存在，并不僅僅存在于加速蠕變階段，高賽紅等[10]認為巖石蠕變過程實質(zhì)是硬化效應和損傷效應相互作用的結(jié)果，損傷效應積累導致巖石塑性蠕變發(fā)展，從而塑性蠕變貫穿整個蠕變過程；若僅僅在加速蠕變階段考慮巖石的塑性蠕變，而在衰減階段則直接利用低應力作用下黏彈性模型，勢必會導致巖石衰減階段的蠕變誤差較大；同時，通過參數(shù)整體擬合得到的加速蠕變模型參數(shù)與實際參數(shù)存在 差異。因此，本文將瞬彈性、黏彈性、黏塑性應變分開進行擬合，不僅能充分考慮衰減蠕變階段的黏塑性應變，而且可得到加速蠕變階段更為真實參數(shù)變化規(guī)律，由此建立的蠕變模型能更好地反映巖石蠕變的非線性特征。

巖石黏塑性蠕變可以采用冪律型函數(shù)式(26)進行擬合，擬合的相關(guān)參數(shù)見表7。

由于巖石在加速蠕變階段，顆粒體間的聯(lián)結(jié)強度減弱，巖石軟化效應增強，導致顆粒體大量定向排列和面?面接觸使得黏結(jié)能力減弱，顆粒流變速率的規(guī)律性減弱[22]。所以，黏塑性應變擬合相關(guān)性相對于黏彈性階段較差。

由此可得巖石黏塑性黏滯系數(shù)dc(,)計算式為

表7 黏塑性應變擬合參數(shù)

4 優(yōu)化模型及驗證

分別對高應力作用下巖石蠕變瞬彈、黏彈、黏塑性應變進行分析，建立瞬彈、黏彈性變形模量的損傷因子和黏塑性黏滯系數(shù)函數(shù)，引入修正變量對模型進行優(yōu)化。改進的模型見圖16，模型方程為

圖16 改進的模型

通過式(28)對各級應力的蠕變實驗結(jié)果進行擬合，部分擬合曲線見圖17，從圖17可知：各級應力作用下優(yōu)化模型與實驗結(jié)果擬合較好，優(yōu)化的模型能很好地反映巖石蠕變?nèi)^程的非線性特征，可為深埋硐室設(shè)計和施工提供參考。

應力/ MPa：(a) 40；(b) 60；(c) 80；(d) 100

5 結(jié)論

1) 采用巖石蠕變破壞前的穩(wěn)態(tài)蠕變速率平均值作為速率閾值，并結(jié)合穩(wěn)態(tài)蠕變速率與應力水平的函數(shù)關(guān)系，得到巖石的長期強度為68.82 MPa，為單軸抗壓強度的74.80%；由該方法推測巖石長期強度比較簡單，可為確定巖石長期強度提供參考。

2) 通過將蠕變曲線中黏彈性、黏塑性應變進行分析，發(fā)現(xiàn)高應力作用下泥質(zhì)粉砂的衰減蠕變階段具有黏彈塑性特征，黏塑性應變隨時間和應力非線性增大，故研究高應力作用下巖石蠕變非線性特征應考慮衰減階段塑性變形的影響。

3) 根據(jù)損傷定義，建立了巖石瞬彈性、黏彈性參數(shù)的損傷方程和黏塑性黏滯系數(shù)函數(shù)，引入修正變量的蠕變模型能很好反映高應力作用下巖石蠕變?nèi)^程的非線性特征。

[1] 王路軍, 周宏偉, 榮騰龍, 等. 深部煤體非線性蠕變本構(gòu)模型及實驗研究[J]. 煤炭學報, 2018, 43(8): 2196?2203. WANG Lujun, ZHOU Hongwei, RONG Tenglong, et al. Research on Experimental and nonlinear creep constitutive model of coal at depth[J]. Journal of China Coal Society, 2018, 43(8): 2196?2203.

[2] 王更峰. 炭質(zhì)板巖蠕變特性研究及其在隧道變形控制中的應用[D]. 重慶: 重慶大學土木工程學院, 2012: 6?8. WANG Gengfeng. Creep characteristics of carbonaceous slate and its application in tunnel deformation control[D]. Chongqing: Chongqing University. School of Civil Engineering, 2012: 6?8.

[3] 汪斌, 朱杰兵, 鄔愛清, 等. 高應力下巖石非線性強度特性的實驗驗證[J]. 巖石力學與工程學報, 2010, 29(3): 542?548. WANG Bin, ZHU Jiebing, WU Aiqing, et al. Experimental verification of rock nonlinear strength characteristics under high stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 542?548.

[4] 朱杰兵. 高應力下巖石卸荷及其流變特性研究[D]. 武漢: 中國科學院研究生院(武漢巖土力學研究所), 2009: 84?88. ZHU Jiebing. Study on unloading and rheological properties of rock under high stress[D]. Wuhan: Graduate School of Chinese Academy of Sciences(Wuhan Institute of Geotechnical Mechanics), 2009: 84?88.

[5] 昝月穩(wěn), 俞茂宏, 趙堅, 等. 高應力狀態(tài)下巖石非線性統(tǒng)一強度理論[J]. 巖石力學與工程學報, 2004, 23(13): 2143?2148. ZAN Yuewen, YU Maohong, ZHAO Jian, et al. Rock nonlinear unified strength theory under high stress state[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(13): 2143?2148.

[6] 楊文東, 張強勇, 陳芳, 等. 輝綠巖非線性流變模型及蠕變加載歷史的處理方法研究[J]. 巖石力學與工程學報, 2011, 30(7): 1405?1413. YANG Wendong, ZHANG Qiangyong, CHEN Fang, et al. Research on nonlinear rheological model of diabase and treatment for creep loading history[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1405?1413.

[7] 宋勇軍, 雷勝友, 韓鐵林. 一種新的巖石非線性黏彈塑性流變模型[J]. 巖土力學, 2012, 33(7): 2076?2080. SONG Yongjun, LEI Shengyou, HAN Tielin. A new nonlinear viscoelasto-plastic rheological model for rocks[J]. Rock and Soil Mechanics, 2012, 33(7): 2076?2080.

[8] 王軍保, 劉新榮, 王鐵行. 基于改進分數(shù)階黏滯體的巖石非線性蠕變模型[J]. 中南大學學報(自然科學版), 2015, 46(4): 1461?1467. WANG Junbao, LIU Xinrong, WANG Tiehang. A nonlinear creep model for rocks based on modified fractional viscous body[J]. Journal of Central South University(Science and Technology), 2015, 46(4): 1461?1467.

[9] 張治亮, 徐衛(wèi)亞, 王偉. 向家壩水電站壩基擠壓帶巖石三軸蠕變實驗及非線性黏彈塑性蠕變模型研究[J]. 巖石力學與工程學報, 2011, 30(1): 132?140. ZHANG Zhiliang, XU Weiya, WANG Wei. Triaxial creep test and nonlinear viscoelastic-plastic creep model of rock in compression zone of Xiangjiaba Hydropower Station[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1): 132?140.

[10] 高賽紅, 曹平, 汪勝蓮, 等. 改進的巖石非線性黏彈塑性蠕變模型及其硬化黏滯系數(shù)的修正[J]. 煤炭學報, 2012, 37(6): 936?943. GAO Saihong, CAO Ping, WANG Shenglian, et al. Improved rock nonlinear viscoelastic plastic creep model and correction of hardening viscosity coefficient[J]. Journal of China Coal Society, 2012, 37(6): 936?943.

[11] 康永剛, 張秀娥. 一種改進的巖石蠕變本構(gòu)模型[J]. 巖土力學, 2014, 35(4): 1049?1055. KANG Yonggang, ZHANG Xiue. An improved constitutive model of rock creep[J]. Rock and Soil Mechanical, 2014, 35(4): 1049?1055.

[12] 齊亞靜, 姜清輝, 王志儉, 等. 改進西原模型的三維蠕變本構(gòu)方程及其參數(shù)辨識[J]. 巖石力學與工程學報, 2012, 31(2): 347?355. QI Yajing, JIANG Qinghui, WANG Zhijian, et al. The improvement of the three-dimensional creep constitutive equation and its parameter identification of the Xiyuan model[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 347?355.

[13] LI Wenquan, LI Xiangdong, HAN Bing, et al. Recognition of creep model of layer composite rock mass and its application[J]. Journal of Central South University of Technology, 2007, 14(1): 329?331.

[14] 蔣海飛, 劉東燕, 趙寶云, 等. 高圍壓高水壓條件下巖石非線性蠕變本構(gòu)模型[J]. 采礦與安全工程學報, 2014, 31(2): 284?291. JIANG Haifei, LIU Dongyan, ZHAO Baoyun, et al. Nonlinear creep constitutive model of rock under high confining pressure and high water pressure[J]. Journal of Mining & Safety Engineering, 2014, 31(2): 284?291.

[15] 趙寶云, 劉東燕, 鄭志明, 等. 基于短時三軸蠕變實驗的巖石非線性黏彈塑性蠕變模型研究[J]. 采礦與安全工程學報, 2011, 28(3): 446?451. ZHAO Baoyun, LIU Dongyan, ZHENG Zhiming, et al. Study on nonlinear viscoelastic-plastic creep model of rock based on short time triaxial creep test[J]. Proceedings of Mining & Safety Engineering, 2011, 28(3): 446?451.

[16] 劉新喜, 童慶闖, 侯勇, 等. 高應力泥質(zhì)粉砂巖非線性蠕變損傷模型研究[J]. 中國公路學報, 2018, 31(2): 280?288. LIU Xinxi, TONG Qingchuang, HOU Yong, et al. Research on nonlinear creep damage model of high stress argillaceous siltstone[J]. Acta Sinica Sinica de Highway, 2018, 31(2): 280?288.

[17] 沈明榮, 諶洪菊. 紅砂巖長期強度特性的實驗研究[J]. 巖土力學, 2011, 32(11): 3301?3305. SHEN Mingrong, CHEN Hongju. Testing study of long-term strength characteristics of red sandstone[J]. Rock and Soil Mechanics, 2011, 32 (11): 3301?3305.

[18] 崔旋, 佘成學. 推斷巖石長期強度的黏塑性應變率法研究[J]. 巖石力學與工程學報, 2011, 30(S2): 3899?3904. CUI Xuan, SHE Chengxue. Study of viscoplastic strain rate method to quickly determine long-term strength of rock. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3899?3904.

[19] 李良權(quán), 徐衛(wèi)亞, 王偉, 等. 基于流變實驗的向家壩砂巖長期強度評價[J]. 工程力學, 2010, 27(11): 127?136, 143. LI Liangquan, XU Weiya, WANG Wei, et al. Estimation of long term strength of Xiangjiaba sandstone based on rheological test[J]. Engineering Mechanics, 2010, 27(11): 127?136, 143.

[20] SZCZEPANIK Z, MILNE D, KOSTAKIS K, et al. Long term laboratory strength tests in hard rock[C]// ISRM 2003- Technology Roadmap for Rock Mechanics. Johannesburg: South African Institute of Mining and Metallurgy, 2003: 1179?1184.

[21] 范秋雁, 陽克青, 王渭明. 泥質(zhì)軟巖蠕變機制研究[J]. 巖石力學與工程學報, 2010, 29(8): 1555?1561. FAN Qiuyan, YANG Keqing, WANG Weiming. Study on creep mechanism of muddy soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1555?1561.

[22] 趙延林，曹平，文有道，等. 巖石彈黏塑性流變實驗和非線性流變模型研究[J]. 巖石力學與工程學報, 2008, 27(3): 477?486. ZHAO Yanlin, CAO Ping, WEN Youdao, et al. Study on elasto-viscoplastic rheological test and nonlinear rheological model of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 477?486.

Viscoelastic-plastic creep model of high stress argillaceous siltstone

LIU Xinxi1, 2, LI Shengnan1, 2, XU Zepei1, 2, LI Yu1, 2, GAO Xuewen1, WANG Weiwei1

(1. School of Civil Engineering Changsha University of Science and Technology, Changsha 410114, China; 2. Hunan Province Engineering Laboratory of Bridge Structure Changsha University of Science & Technology, Changsha 410114, China)

In order to reveal the rheological characteristics of deep buried underground chamber surrounding rock under high stress, triaxial compression creep test was carried out on argillaceous siltstone by incremental loading method. According to the relationship between steady-state creep rate and stress, the long-term strength of rock was determined by using a given creep rate threshold. Considering the characteristics of creep curve, the function relationship among the parameters of model, stress level and time was established based on separation of instantaneous elasticity viscoelastic, and viscoplastic strain from creep curves. According to the damage definition, the damage variables of instantaneous elastic element and viscoelastic element were determined, and the Nishihara model was optimized by introducing instantaneous elasticity, viscoelastic damage variable and viscoplastic correction coefficient, which could describe the whole process of rock creep under high stress. The results show that the steady creep rate increases exponentially with the increase of stress. The long-term strength of rock obtained by the given creep rate threshold is 68.82 MPa, which is 74.80% of the uniaxial compressive strength. The creep model established based on strain viscoelastic-plastic separation can well describe the nonlinear characteristics of the whole process of rock creep, and the fitting between the optimizedmodel and the experimental data is good, which proves the rationality of the creep model.

rock mechanics; argillaceous siltstone; creep test; creep model; nonlinear

U416

A

1672?7207(2019)05?1210?11

10.11817/j.issn.1672-7207.2019.05.025

2018?08?30；

2018?10?22

國家自然科學基金資助項目(51378082，51674041)；長沙理工大學橋梁結(jié)構(gòu)安全控制湖南省工程實驗室基金資助項目(18KD04)；湖南省研究生科研創(chuàng)新項目(CX2018B532) (Projects(51378082, 51674041) supported by the National Natural Science Foundation of China; Project(18KD04) supported by Open Fund of Engineering Laboratory of Bridge Structure Changsha University of Science & Technology of Hunan Province; Project(X2018B532) supported by Innovation Foundation of Postgraduate of Hunan Province)

李盛南，博士研究生，從事巖土工程研究，E-mail：2561720910@qq.com

(編輯 陳燦華)