水泥回轉窯物料流動與傳熱特性數值模擬

劉彬，周武洲，趙朋程，李瑞

?

水泥回轉窯物料流動與傳熱特性數值模擬

劉彬，周武洲，趙朋程，李瑞

(燕山大學 電氣工程學院，河北 秦皇島,066004)

針對回轉窯煤粉燃燒過程中物料運動和傳熱特性難以仿真分析的問題，將回轉窯看作是由高溫煙氣流域和物料流域組成且相互耦合的計算域。在壁面?zhèn)鳠岬幕A上，利用熱傳導方程描述不同區(qū)域物料經窯壁向外散熱的熱流密度，并提出一種帶傳熱補償的物料和高溫煙氣的換熱模型。采用此模型數值模擬回轉窯內的煤粉燃燒、物料流動和燒結等，研究不同工況下物料流動和溫度分布情況。研究結果表明：所建模型可以較準確地反映物料在回轉窯內的傳熱和運動情況；回轉窯轉速的升高會增大物料沿軸向運動的加速度；增加回轉窯內物料流量會降低物料溫度，并加劇物料表層和內部的溫度差；物料填充率的增加會擴大外回流區(qū)的范圍，升高冷卻帶的溫度；當物料填充率達到12%時會引發(fā)康達效應，使回轉窯火焰在靠近物料區(qū)域向物料方向發(fā)生偏移。

計算流體力學；多相流；傳熱；數值模擬；煤燃燒

在水泥生產過程中，回轉窯內的熟料燒結溫度直接影響水泥質量，研究回轉窯的運行參數影響熟料溫度分布機理對提高水泥質量和降低生產能耗等有著重要意義[1–2]。近年來，隨著計算機計算能力的不斷提高以及計算流體力學仿真軟件的不斷完善，大量學者采用數值模擬方法分析回轉窯內的煤粉燃燒機理或物料的流動與傳熱特性[3–4]，如ELATTAR等[5]建立回轉窯二維模型，研究了主要操作對不同燃料下回轉窯內火焰行為的影響；WANG等[6]建立了回轉窯和燃燒器三維模型，在不考慮回轉窯斜度和物料的情況下，研究入窯空氣含氧量對火焰溫度的影響；GAIKWAD[7]等建立了簡化的回轉窯CFD模型，采用DO模型與加權和灰度氣體方法耦合的輻射熱傳遞模型，研究空氣、氧含量等燃燒環(huán)境對火焰溫度和氮氧化物濃度分布的影響；陳輝等[8]采用離散單元法，以球形砂礫模擬回轉窯內的物料流動，通過數值模擬實驗研究物料的運動模式與力鏈結構；胡陳樞等[9]建立了滾筒的二維數值模型，研究不同滾筒轉速下，2組顆粒的混合和分離情況，并提出2種衡量顆粒混合程度的評價函數；王擎等[10]建立了回轉干餾爐的二維模型，研究回轉干餾爐內顆粒的運動和傳熱特性；YIN等[11–12]在不考慮煤粉燃燒的前提下，研究了回轉窯傾斜角和轉速對窯內物料停留時間和流速的影響，而且研究了風道流速對煤粉分布的影響；MA等[13]利用商業(yè)CFD軟件，對裝備四通道旋流燃燒器的回轉窯進行數值模擬，分析了不同工況下窯內流場與溫度場分布、氮氧化物生成和火焰的特點；KLIMANEK等[14]利用歐拉–拉格朗日多相流的方法研究了碳顆粒在流化床中的分布，分析了介質對碳顆粒氣化反應的影響，DELELE等[15]利用歐拉–歐拉多相流方法建立了三維多相流模型，分析了物料填充率、物料進口速度和圓筒轉速等工況條件對物料顆粒和氣體的流動行為的影響。然而由于回轉窯內部是典型的多相流，多相流模型在模擬煤粉燃燒和追蹤離散相顆粒方面的精度難以達到研究所需的要求[16]，且多相流在模擬煤粉燃燒過程中計算量大，難以收斂[17]。前人只針對回轉窯內的高溫煙氣流域而不考慮物料相，或者是只針對回轉窯內的冷態(tài)物料流體流動而不考慮煤粉燃燒的影響。為解決多相流模型難以模擬煤粉燃燒的問題，王春華等[18]將回轉窯內的流域劃分為氣體空間和物料料層2個計算域，用FLUENT模擬回轉窯內的煤粉燃燒，將相關仿真數據導入到MATLAB中模擬物料溫度分布。MUJUMDAR等[19–20]提出將熟料看作一種偽流體，分別對回轉窯內的高溫煙氣流域和物料流域進行三維建模，利用CFD軟件對兩流域進行仿真，每間隔次仿真迭代，將2個模型中交界面數據對比后進行數據交換，直到兩者數據對比一致。但是，上述研究由于將2個計算域依次分開進行模擬，降低了仿真結果的可靠性。為了解決在回轉窯內模擬煤粉燃燒，同時難以對物料流體進行仿真的問題，本文建立2個相互耦合的計算域。考慮到計算域之間的輻射換熱和實際情況相比存在額外的熱阻耗散，所以，本文在壁面換熱的基礎上，提出一種帶輻射換熱補償的物料和高溫煙氣的換熱模型，通過編寫UDS程序將該換熱模型應用到仿真過程中，在所建立的換熱模型基礎上，研究回轉窯轉速、物料流速和物料填充率對物料運動和溫度的影響。

1 幾何模型

根據燃燒器和回轉窯的實際尺寸建立三維幾何模型，回轉窯的內部物料燒結如圖1所示，水泥回轉窯煅燒系統(tǒng)可以大致可分為煤粉燃燒器和回轉窯窯體2個部分，一次風和煤粉顆粒經由燃燒器噴入回轉窯內形成高溫火焰，高溫二次風進入回轉窯為煤粉燃燒進行預熱并提供氧氣，物料在經過預分解之后由窯尾進入回轉窯，回轉窯內的物料經過過渡帶的預熱，進入鄰近火焰的高溫燒成帶，物料在燒成帶中發(fā)生一系列復雜的化學反應，之后經過冷卻帶流出回轉窯進入篦冷機。

圖1 回轉窯內部物料燒結示意圖

本文采用目前在水泥生產領域廣泛使用的四通道旋流燃燒器建立如圖2所示的幾何模型。回轉窯幾何模型由燃燒器和回轉窯窯體2個部分組成。

圖 2 四通道旋流燃燒器模型示意圖

回轉窯的窯體幾何模型參考實際生產尺寸，設置直徑為4.0 m，高度70 m。由于本文不考慮回轉窯耐火磚厚度，實際回轉窯內徑設置為3.6 m。在實際水泥生產中，回轉窯斜度一般為3%~4%，本文將回轉窯窯體的斜度設置為3.5%。

在回轉窯窯體的幾何模型建立過程中，將回轉窯窯體分為2個幾何模型：一個幾何模型作為煙氣流體的計算域，另一個作為物料流體的計算域。這2個計算域由交界面進行耦合計算，以解決煤粉燃燒和物料流動同時進行仿真時計算量大、難以收斂等問題。物料流域建模過程不考慮由于傾斜角和轉速引起的厚度變化，交界面沿窯軸向方向長度設置為相同。

建立回轉窯燒結系統(tǒng)的幾何模型后，采用3種不同的網格步長，對物料填充率為12%的回轉窯模型進行網格劃分，得到網格數分別為410 234，503 114和620 189個，以便后續(xù)驗證網格無關性。回轉窯系統(tǒng)網格模型如圖3所示。

2 邊界條件與數學模型

模擬回轉窯內部流場環(huán)境需要1個多相(氣體、煤粉顆粒、物料流體)混合流模型模擬，而多相流模型在模擬離散相時計算精度低、難以收斂，本文將回轉窯內的高溫煙氣和物料分為2個由交界面連接的計算域。在煙氣流域中，應用離散相模型(DPM)追蹤煤粉顆粒軌跡，煤粉燃燒、湍流和輻射模型分別選用非預混燃燒模型、標準–模型以及離散坐標DO輻射 模型。

圖 3 回轉窯系統(tǒng)網格模型

2.1 邊界條件

回轉窯中物料呈現復雜的流動運動狀態(tài)，即使以現在的CFD技術仍然難以精確地模擬物料運動的細節(jié)，胡陳樞等[9]指出回轉窯中物料可以用均質流體來近似處理。因此，在物料流域內，忽略物料在回轉窯內的化學反應，用氧化鈣流體材料近似代替回轉窯內的物料。

為更準確地模擬回轉窯轉動，將物料計算域的壁面設置為旋轉無滑移壁面，設置標準工況下回轉窯轉速為0.05 rad/s，總煤流量為2.46 kg/s，回轉窯斜度為3.5%，氧含量為23.15%，回轉窯轉速為0.05 rad/s，物料填充度為12%。標準工況下的具體邊界條件設置見表1。煤粉顆粒直徑服從Rosin-Rammler分布，并設置9組不同直徑的煤粉顆粒，不同顆粒直徑的煤粉的流量如圖4所示。

表1 標準工況邊界條件參數

圖4 不同煤粉顆粒直徑流量分布

2.2 物料流域的控制方程與源項

由于熟料流動緩慢，交界面平整，所以，可以將兩相流換熱看作為流體和固體壁面間的換熱，在壁面附近的流體一側，傅里葉定律成立，本文以氣固兩相流之間的交界面和物料流域為研究對象建立氣固兩相流的對流換熱數學模型。同時，由于物料與交界面直接接觸，所以，在物料一側的交界面與物料之間不存在輻射換熱。另一方面，由于物料和窯壁直接接觸，物料會和窯壁發(fā)生熱傳導散熱。因此，對于水泥回轉窯中的物料，其主要的換熱形式包括與高溫煙氣之間的對流換熱以及與回轉窯窯壁之間的傳導換熱。物料的流動與換熱簡化模型如圖5所示。

圖5 物料傳熱模型

本文將物料流域和高溫煙氣流域分開，2個區(qū)域之間不存在物質交換，故質量源項為零。本文采用的能量方程形式如下：

式中：為微元體的內能；eff為有效導熱系數；能量源項E=0；為微元體密度。

2.2.1對流換熱模型

由熱力學第一定律可知，單位時間微元體內能的增量加上傳出控制體的能量與傳入之差，等于作用于控制體上各個力所作的功。考慮能量隨時間的變化，單位時間微元體內的能量變化方程表達式如下：

式中：是物料的速度；，和分別為物料在，和軸上的速度分量。

由納維–斯托克斯方程方程可知方向上的動量滿足如下方程：

式中：為物料動量；為物料動力黏度；t為物料湍流動力黏度。

同理可得和方向上的動量方程。本文假設回轉窯內的流體為不可壓縮流體，其動力黏度和其湍流動力黏度t均為常數，所以，式(3)可以簡化如下：

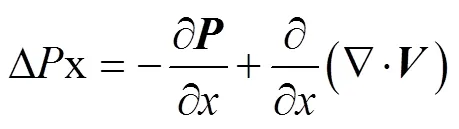
在上述能量方程和動量方程基礎上，用自定義函數程序編寫定義源項。在物料計算域的源項設置中為，和這3個方向上動量以及能量分別添加各自的源項。

2.2.2 對流換熱補償

由于耦合壁面的加入，使高溫煙氣和物料之間的熱阻數量增加，為避免影響仿真計算的準確性，需要進行換熱補償。兩耦合壁面之間不存在熱阻，可將高溫煙氣經過耦合壁面到物料的換熱過程，看作2個串聯(lián)的熱阻。該傳熱過程是穩(wěn)態(tài)過程，通過串聯(lián)著的2個熱阻環(huán)節(jié)的熱流量必定相等。由牛頓冷卻公式可知2個環(huán)節(jié)的熱流量表達式如下：

式中：為熱流量；1為鄰近高溫煙氣流域壁面的傳熱系數；2為鄰近物料流域壁面的傳熱系數；為微元體與耦合壁面相連面的表面積；q為鄰近耦合壁面的高溫煙氣溫度；s為鄰近耦合壁面的物料微元溫度；w1和w2分別為耦合壁面上、下壁面的溫度，且w1=w2。

聯(lián)立式(5)和式(6)，消去w1和w2，得到熱流量的表達式為

在不存在耦合壁面時，高溫煙氣和物料之間的熱流量s如下：

式中：為物料的傳熱系數。

聯(lián)立式(7)和式(8)可知，為補償由耦合壁面所產生的熱阻耗散，以使s=，可設12=2。

老陸變化太大了。看上去比你還要老（我老嗎？），頭發(fā)都掉光了，禿腦門兒。上學那會，也算是個帥哥，現在整個一老頭模樣，簡直不敢認了。你知道他是做什么的嗎，教育局當處長，你知道他開的什么牌子的車，奧迪Q 5，我操，六七十萬吧！

2.2.3熱傳導模型

緊鄰窯壁的物料顆粒會因摩擦力的存在而與窯壁同步旋轉，由于二者之間無相對運動，所以，將物料和窯壁之間的傳熱方式看作熱傳導。通過實時計算回轉窯壁和物料之間的熱流密度，實現物料經窯壁向外的散熱模擬。為簡化計算，將與物料接觸的窯壁按軸向距離分為70個區(qū)域，并分別計算每個區(qū)域內的平均熱流密度。物料流域部分各處窯壁的熱流密度X可以用 下式表示：

式中：x為距窯頭x m區(qū)域內回轉窯窯壁的平均溫度；為室溫；r為耐火磚導熱系數；為回轉窯窯壁厚度。

通過仿真軟件數據接口讀取并計算式(9)所需的物料平均溫度，利用UDF編寫物料流域窯壁的熱流密度函數，實現與物料接觸窯壁的熱流密度隨著仿真迭代的增加而實時變化。

3 結果與討論

在進行數值模擬仿真實驗之前，首先對所建立的3組網格模型進行網格無關性驗證，邊界條件均按表1設置，并對3組網格模型進行仿真計算，計算結果如表2所示。

冀東水泥控制二次風溫在1 323 K左右，現場檢測窯尾溫度在1 267~1 417 K范圍內浮動，從表2可知：現場所得結果與后2組仿真結果相吻合，證明所建模型具有可靠性。綜合考慮計算精度和計算量的要求，本文選擇網格數量為503 114個的網格步長劃分網格。

表2 網格無關性驗證結果

在分析回轉窯內物料燒成效果時，引入溫度標準差概念，來評價回轉窯物料流域內橫截面上的物料溫度分布的離散程度，定義溫度標準差為

為便于數據處理，設置每個橫截面區(qū)域的縱向寬度為1 m，橫截面區(qū)域劃分示意圖如圖6所示。

圖6 物料橫截面區(qū)域劃分示意圖

3.1 回轉窯轉速對物料燒成的影響

回轉窯窯體的轉動有助于增加物料顆粒的擾動，使物料能整體受熱，并且促進物料的流動和顆粒之間的換熱，圖7所示為工況下物料顆粒的流動軌跡，物料顆粒呈螺旋狀向窯頭流動。圖8所示為工況條件下窯頭溫度分布輪廓圖。

為了研究回轉窯轉速對窯內物料溫度分布和運動狀態(tài)的影響，分別設置回轉窯轉速為0.01，0.02和0.03 rad/s，并保持其余工況條件不變，進行數值模擬計算。

圖7 工況條件下物料顆粒流動軌跡

圖8 工況條件下窯頭溫度輪廓

圖9所示為不同回轉窯轉速下，物料橫截面區(qū)域上的溫度標準差。從圖9可見：當回轉窯轉速為0.01 rad/s時，物料的溫度分布離散化程度最高，隨著回轉窯轉速的提高，回轉窯內的物料顆粒的擾動增強，物料得到更充分混合，溫度分布離散程度降低；當回轉窯轉速固定時，隨著物料由窯尾向窯頭的流動，物料的溫度離散程度呈下降趨勢。窯頭附近處于冷卻帶，物料溫度的離散程度的波動加劇，由傅里葉定律可知，該區(qū)域的熱流方向改變，物料開始向空氣散熱，所以，物料溫度的離散程度波動加劇。

圖9 回轉窯轉速對物料溫度標準差分布的影響

圖10所示為不同回轉窯轉速下，物料流速沿軸分量的分布圖。從圖10可見：隨著回轉窯轉速的增加，物料流動的加速度增大；當轉速為0.01 rad/s時，物料流速增加緩慢，物料內部的動能耗散造成物料流速比設定值小。

圖10 回轉窯轉速對物料流速分布的影響

在物料剛入窯時，由于壁面函數采用無滑移邊界條件，底層物料流速會隨回轉窯轉動而運動，底層物料和上層物料的運動方向不同，而黏性力和物料之間的相對速度變化率呈正相關關系，因此，物料在剛入窯時處于非穩(wěn)態(tài)，速度變化率大，其所受的黏性力也較大。隨著物料的流動，底層物料和上層物料之間的流速差減小，物料之間的黏性力減小，不足以與體積力達到平衡，導致物料呈加速流動狀態(tài)。

3.2 物料流量的影響

在研究物料流量對物料運動及其溫度分布的影響時，設置3組不同的物料流量，分別為0.6，0.7和 0.8 m/min，其余工況條件按表1設置。

圖11所示為不同物料流速下物料溫度標準差。從圖11可以看出：物料流速增加會導致其溫度離散程度加大，這是因為物料流速的升高會減小物料在同一橫截面區(qū)域的停留時間，物料受熱時間變短，溫度標準差變大。

圖12所示為不同物料流速下，物料顆粒沿軸方向上的速度分量的分布圖。由圖12可以看出：在相同回轉窯轉速下，物料顆粒在回轉窯中沿軸方向的加速度保持不變，速度分量與入窯的初始速度成正比。這表明物料顆粒在回轉窯中沿軸向流動的加速度與回轉窯轉速正相關，而與物料顆粒入窯的初始流速無關。

圖11 物料流速對物料溫度標準差分布的影響

圖12 初始物料流速對物料流速分布的影響

圖13所示為不同物料入口流速下，物料橫截面區(qū)域平均溫度的分布圖。從圖13可以看出：隨著物料入口流速的增加，物料整體溫度分布降低；物料流速的增加導致物料在回轉 窯內的停留時間變短，進而造成物料的平均溫度降低，然而物料流量的增加可以提高回轉窯的生產效率。故經綜合考慮，最佳的物料流速應在0.6~0.7 m/min之間。

3.3 物料填充率的影響

物料填充率是決定水泥生產質量和效率的關鍵因素之一，也會對回轉窯內的高速氣流的流向產生不可忽略的影響。為分析物料填充率對物料傳熱和回轉窯內高溫煙氣流場的影響，分別建立3種不同物料填充率的幾何模型，在相同的邊界條件下進行仿真計算。

圖13 物料流速對物料平均溫度的影響

圖14所示為不同物料填充率下的物料溫度標準差分布圖。從圖14可見：隨著物料填充率的增加，物料溫度標準差顯著變大，這說明物料填充率的增加會加劇物料溫度在垂直方向上的離散程度。

圖14 不同填充率下物料溫度標準差

圖15所示為不同物料填充率下物料的溫度分布圖。從圖15可見：隨著物料填充率的增加，物料的峰值溫度位置逐漸向窯頭靠近；隨著物料填充率的增加，物料表面層距離燃燒器噴射的高速氣流變近，當靠近到一定距離時，由于康達效應影響，高速氣流的流動方向會向物料偏移；此外，隨著物料填充率的增加，物料在冷卻帶的溫度下降趨勢變緩。不同物料填充率下的窯頭濕度輪廓見圖16。對比圖16和標準物料填充率下的窯頭溫度輪廓可以看出：隨著物料填充率的增加，火焰和物料之間的外回流區(qū)逐漸擴大，下游的高溫煙氣被卷吸到冷卻帶，導致冷卻帶溫度升高，使物料在冷卻帶的溫度下降趨勢變緩。圖17所示為不同填充率下，分別距離窯頭3，6和9 m處物料的溫度輪廓圖。從圖17可以直觀地看出隨著物料填充率的增加，物料表面散熱減少。冷卻帶溫度過高會導致物料在進入篦冷機時凝結成塊，嚴重影響水泥質量，為避免康達效應對物料燒成過程和火焰的影響，應該避免物料填充率過大。

圖15 不同填充率下物料溫度分布

物料填充率：(a) 9%; (b) 15%

物料填充率: (a) 9%; (b) 12%; (c) 15%

4 結論

通過建立回轉窯內物料和高溫煙氣的換熱模型以及回轉窯窯壁和物料之間的熱傳導模型，建立包含高溫煙氣和水泥物料的回轉窯內部CFD模型，利用FLUENT軟件，研究不同工況下的回轉窯模擬實驗，證明模型的合理性。

1) 隨著回轉窯轉速的升高，物料的混合程度更均勻，物料橫截面區(qū)域的溫度離散程度明顯降低，且物料在回轉窯內沿軸向流動的加速度增大，使物料的燒結效率提高。

2) 物料流速的增加會降低物料整體溫度，并加大表層物料溫度的內部物料的溫度差，物料流量過高不利于物料的燒結，合理的物料流速為0.6~0.7 m/min。

3) 物料填充率的增加，會擴大外回流區(qū)的區(qū)域，進而導致物料在冷卻帶區(qū)域的冷卻效果降低；當填充率達到15%時，回轉窯火焰出現明顯的康達效應，冷卻帶的范圍縮短，出窯物料溫度升高，影響熟料的質量，合理的物料填充率為12%左右。

[1] BENHELAL E, ZAHEDI G, SHAMSAEI E, et al. Global strategies and potentials to curb CO2, emissions in cement industry[J]. Journal of Cleaner Production, 2013, 51(1): 142?161.

[2] ATMACA A, YUMRUTA? R. Analysis of the parameters affecting energy consumption of a rotary kiln in cement industry[J]. Applied Thermal Engineering, 2014, 66(1/2): 435?444.

[3] SAIDUR R, HOSSAIN M S, ISLAM M R, et al. A review on kiln system modeling[J]. Renewable & Sustainable Energy Reviews, 2011, 15(5): 2487?2500.

[4] MIKUL?IC H, BERG E V, VUJANOVIC′ M, et al. Numerical study of co-firing pulverized coal and biomass inside a cement calciner.[J]. Waste Management & Research, 2014, 32(7): 661.

[5] ELATTAR H F, STANEV R, SPECHT E, et al. CFD simulation of confined non-premixed jet flames in rotary kilns for gaseous fuels[J]. Computers & Fluids, 2014, 102: 62?73.

[6] WANG Mingyue, LIAO Bin, LIU Yiqin, et al. Numerical simulation of oxy-coal combustion in a rotary cement kiln[J]. Applied Thermal Engineering, 2016, 103: 491?500.

[7] GAIKWAD P, KULKARNI H, SREEDHARA S. Simplified numerical modelling of oxy-fuel combustion of pulverized coal in a swirl burner[J]. Applied Thermal Engineering, 2017, 124: 734–745.

[8] 陳輝, 劉義倫, 肖友剛, 等. 回轉窯截面物料運動及力鏈結構的數值試驗[J]. 中南大學學報(自然科學版), 2015, 46(7): 2446–2451. CHEN Hui, LIU Yilun, XIAO Yougang, et al. Numerical experiments on transverse motion and force chains of solids in rotating cylinders[J]. Journal of Central South University(Science and Technology), 2015, 46(7): 2446–2451.

[9] 胡陳樞, 羅坤, 樊建人, 等. 滾筒內二組元顆粒混合與分離的數值模擬[J]. 工程熱物理學報, 2015, 36(9): 1947?1951.HU Chenshu, LUO Kun, FAN Jianren, et al. Mixing and segregation of binary particles in rotating drum: a numerical study[J]. Journal of Engineering Thermophysics, 2015, 36(9): 1947?1951.

[10] 王擎, 李建, 王智超, 等.回轉干餾爐內顆粒間傳熱特性的數據模擬[J]. 化工學報, 2017, 68(11): 4137?4146. WANG Qing, LI Jian, WANG Zhichao, et al. Numerical simulation on characteristics of heat transfer between particles in rotary retorting[J]. Journal of Chemical Industry and Engineering(China). 2017, 68(11): 4137?4146.

[11] YIN Hongchao, ZHANG Ming, LIU Hong. Numerical simulation of three-dimensional unsteady granular flows in rotary kiln[J]. Powder Technology, 2014, 253(2): 138?145.

[12] 尹洪超, 沈春艷, 劉紅,等. 回轉窯冷態(tài)射流和氣固兩相流數學計算[J]. 硅酸鹽學報, 2013(11): 1527?1533. YIN Hongchao, SHEN Chunyan, LIU Hong, et al. Calculation of cold jet and gas–solid two phase flow in rotary kiln[J]. Journal of the Chinese Ceramic Society, 2013(11): 1527?1533.

[13] MA Aichun, ZHOU Jiemin, OU Jianping, et al. CFD prediction of physical field for multi-air channel pulverized coal burner in rotary kiln[J]. Journal of Central South University of Technology, 2006, 13(1): 75–79.

[14] KLIMANEK A, ADAMCZYK W, KATELBACH-WO?NIAK A, et al. Towards a hybrid Eulerian–Lagrangian CFD modeling of coal gasification in a circulating fluidized bed reactor [J]. Fuel, 2015, 152: 131?137.

[15] DELELE M A, WEIGLER F, FRANKE G, et al. Studying the solids and fluid flow behavior in rotary drums based on a multiphase CFD model[J]. Powder Technology, 2016, 292: 260?271.

[16] WEN Xu, LUO Yujian, LUO Kun, et al. LES of pulverized coal combustion with a multi-regime flamelet model[J]. Fuel, 2017, 188: 661?671.

[17] MARIAS F, ROUSTAN H, PICHAT A. Coupling between CFD and a bed model in a rotary kiln: application to the processing of aluminium waste[J]. Progress in Computational Fluid Dynamics An International Journal, 2007, 7(1): 40?50(11).

[18] 王春華, 陳文仲, 賈馮睿,等. 回轉窯內傳熱及燃燒過程的數值模擬[J]. 化工學報, 2010, 61(6):1379?1384. WANG Chunhua, CHEN Wenzhong, JIA Fengrui, et al. Numerical simulation of heat transfer and combustion in carbon rotary kiln[J]. Journal of Chemical Industry and Engineering(China), 2010, 61(6): 1379?1384.

[19] MUJUMDAR K S, RANADE V V. CFD modeling of rotary cement kilns[J]. Asia-Pacific Journal of Chemical Engineering, 2010, 3(2): 106?118.

[20] MUJUMDAR K S, GANESH K V, KULKARNI S B, et al. Rotary cement kiln simulator (RoCKS): Integrated modeling of pre-heater, calciner, kiln and clinker cooler[J]. Chemical Engineering Science, 2007, 62(9): 2590–2607.

Numerical simulation of material flow and heat transfer characteristics of cement rotary kiln

LIU Bin, ZHOU Wuzhou, ZHAO Pengcheng, LI Rui

(School of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China)

According to the analysis of material movement and heat transfer characteristics in the process of pulverized coal combustion, the rotary kiln was considered as a calculation field composed of high-temperature flue gas flow and material flow, which were coupled with each other. Based on heat transfer on the wall surface, heat flow equation was used to describe heat flux of the material through kiln wall. A heat transfer model with heat transfer compensation was proposed to describe the heat transfer between material and high-temperature flue gas. This model was used to simulate the combustion of pulverized coal, material flow and sintering in the rotary kiln. In addition, flow and temperature distribution of the material under different working conditions were studied. The results show that the heat transfer and movement of the material in the rotary kiln can be accurately reflected by the model. The increase of the rotational speed improves the axial acceleration of the material in the rotary kiln. The increase of material flow rate in the rotary kiln results in the decrease of the temperature of the material, but improves the temperature difference between surface material and internal material. The increase of the material filling rate enlarges the area of the outer recirculation zone and improves the temperature of cooling zone. When the material filling rate reaches 12%, Coanda effect will be induced,causing the rotary kiln flame shift toward material direction near the material area.

computational fluid dynamites(CFD); multiphase flow; heat transfer; numerical simulation; coal combustion

TQ028.8

A

1672?7207(2019)05?1235?09

10.11817/j.issn.1672?7207.2019.05.028

2018?08?30；

2018?12?13

國家自然科學基金資助項目(51641609)；河北省自然科學基金資助項目(E2018203398) (Project(51641609) supported by the National Natural Science Foundation of China; Project(E2018203398) supported by the Natural Science Foundation of Hebei Province)

劉彬，教授，博士生導師，從事燃燒理論與數值模擬研究；E-mail:liubin@ysu.edu.cn

(編輯 秦明陽)