四旋翼直升機的線性自抗擾與非線性H2/H∞混合控制

劉俊杰，高強，孫明瑋，陳增強

(1.南開大學 人工智能學院，天津，300350；2.天津理工大學 電氣與電子工程學院，天津，300384)

無人機(unmanned aerial vehicle，UAV)也稱“無人飛行器”，即不搭載飛行員的空中飛行器[1]。近年來，隨著科學技術尤其是傳感器技術和控制理論的不斷提高[2]， 無人飛行器的發展在自動控制領域引起了人們的高度關注。多種無人飛行器已經被用于執行各類任務，如地面監測、高空航拍、抗震救災、軍事偵察等[3]，因此，開展具有垂直起降功能的高機動性、強穩定性的無人飛行器控制研究在空中機器人領域意義重大。作為一種典型的垂直起降無人飛行器，四旋翼無人直升機結構簡單，通過2對旋翼產生的平衡力實現穩定懸停和改變飛行狀態，并能完成低速飛行等動作[4]。然而，四旋翼直升機的控制量數目少于系統的自由度，屬于欠驅動系統，在實際飛行過程中受諸多因素影響，是一個非線性強、參數不確定、耦合強、對外擾敏感的復雜對象，其跟蹤控制問題成為控制領域的難點和熱點。針對簡化的四旋翼直升機模型，常見的線性算法有PID控制[5-6]、LQR控制[7]以及線性H∞控制[8]。由于四旋翼直升機模型中的強非線性，且在飛行過程中易受非線性阻力的影響，當飛行器遠離平衡點時，線性控制算法可能失效，因此，研究人員使用反步法[9-10]、反饋線性化[11]、滑模控制[12]、浸入和不變控制[13]以及非線性 H∞控制[14]等非線性控制方法進行控制器設計。針對拉格朗日-歐拉方程推導的非線性模型，RAFFO等[14]采用反步法和H∞控制對四旋翼直升機系統中的持續外部擾動進行抑制。MOKHTAR 等[15]考慮四旋翼直升機非線性模型的不確定性，設計非線性H∞輸出反饋控制器，并采用高階滑模觀測器進行擾動估計。RAFFO 等[16]提出一種非線性魯棒控制結構，將四旋翼直升機系統劃分為旋轉運動子系統和平移運動子系統，并采用非線性H∞控制器對旋轉運動進行鎮定，利用模型預測控制實現位置坐標的跟蹤控制。自抗擾控制(active disturbance rejection control，ADRC)是韓京清[17]提出的一種新型實用控制技術，其不依賴系統的精確模型，可直接利用被控對象的輸入輸出信息對系統狀態以及“總擾動”進行估計并在線補償[18]。在此基礎上，GAO[19]將非線性自抗擾控制器中的非線性環節進行線性化處理，極大簡化了ADRC的參數整定方法。目前，自抗擾控制已逐步應用于各個領域，如工業過程[20]、伺服系統[21]、機器人控制[22]等。本文作者針對四旋翼直升機的非線性模型，將其劃分為旋轉運動子系統與平移運動子系統，在考慮持續外部擾動的情況下，利用線性自抗擾控制解決平移運動中系統位置坐標的跟蹤問題；對于四旋翼直升機的旋轉運動，采用一種非線性H2/H∞混合控制方法，在抑制外部干擾的同時保持良好的跟蹤性能。

1 系統模型

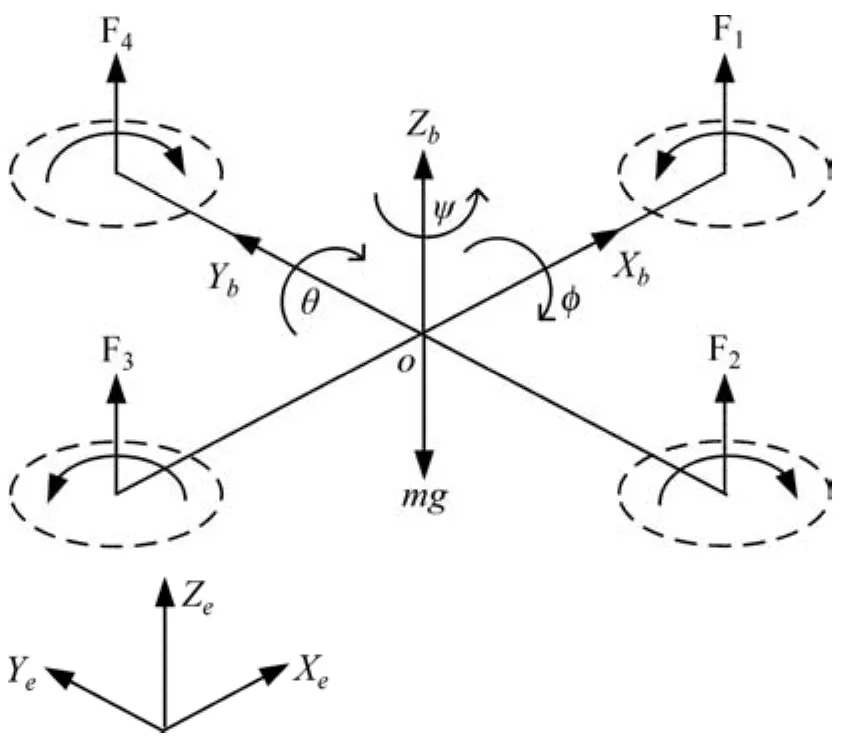
圖1 坐標系示意圖Fig.1 Diagram of coordinate system

坐標系示意圖如圖1所示，四旋翼直升機具有6個自由度。圖1中：Xe=[x,y,z]T，η=[φ,θ,ψ]T，分別表示四旋翼直升機在慣性坐標系中的位置和姿態角(滾轉、俯仰和偏航)；，表示機體坐標系；Xb軸指向飛機前進方向；YbXb正交；Zb垂直于XbOYb并指向上方；地面坐標系為慣性坐標系；姿態角，表示機體坐標系與地面坐標系之間的旋轉關系。考慮到右手坐標系，由繞x，y和z軸的旋轉關系可以得到從機體坐標系到地面坐標系的轉換矩陣Rb為

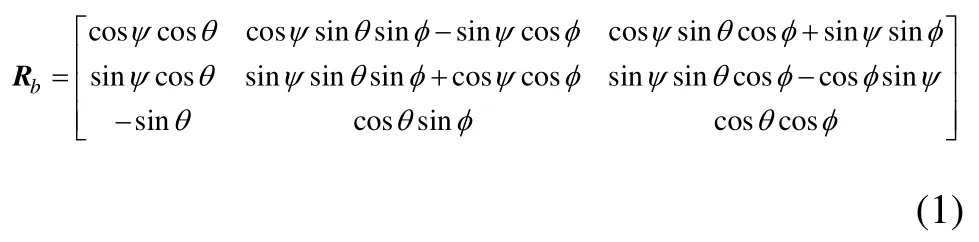
其中：

利用基于動能和勢能的拉格朗日-歐拉方程，可將四旋翼無人飛行器的運動方程表示為[17]

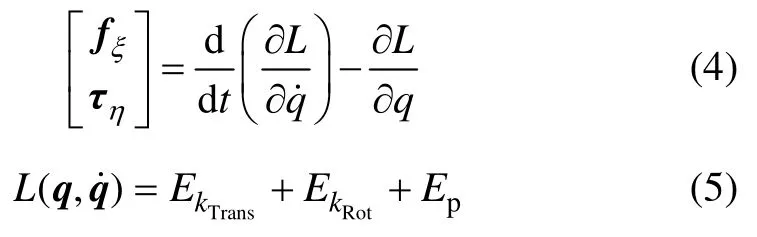
其中：L為四旋翼無人飛行器模型的拉格朗日算子；EkTrans為平移運動動能；EkRot為旋轉運動動能；Ep為系統總勢能。

即

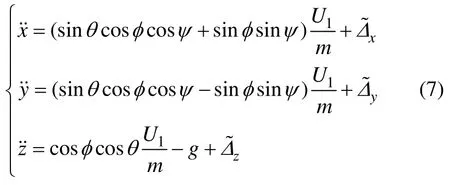
其中：m為機體質量；g為重力加速度；為外部擾動。

定義矩陣N為以下形式：

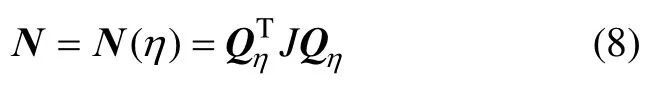
其中：J=diag(Ixx,Iyy,Izz)，為轉動慣量矩陣。則旋轉動能方程可以表示為

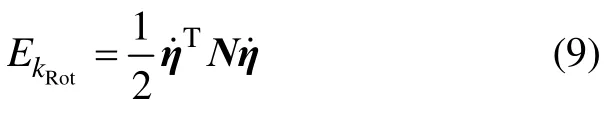
令M(η)=Ν(η)，拉格朗日-歐拉旋轉方程可以重新表示為

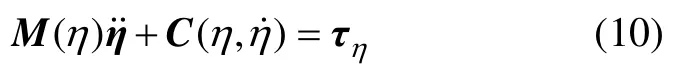
其中：

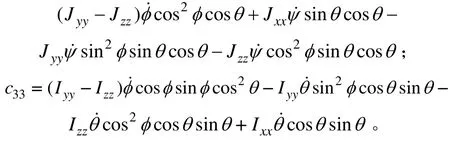
因此，利用拉格朗日-歐拉方程導出的四旋翼直升機旋轉運動的非線性數學模型為

故四旋翼無人直升機的非線性數學模型為

2 控制策略

由四旋翼直升機動力學模型可知，飛行器在飛行過程中控制器直接作用于飛行器姿態角與高度，姿態角又直接影響飛行器的水平位置，因此，飛行控制器多采用內外環的結構。考慮四旋翼無人直升機的參數不確定、未建模動態及外部擾動，設計一種非線性魯棒控制策略，以實現其路徑跟蹤控制，其控制結構如圖2所示。式(13)將四旋翼直升機系統分為旋轉運動和平動運動，為解決四旋翼直升機旋轉運動控制問題，控制結構內環采用一種非線性混合控制方法，在考慮參數不確定性和持續外部擾動的情況下，實現姿態角和姿態角速度的穩定控制。對于平移運動，在控制結構外環采用線性自抗擾控制器，實現四旋翼直升機位置的軌跡跟蹤控制。位置參考信號由參考路徑發生器產生，當考慮未建模動態和持續外部擾動時，對所設計的線性自抗擾控制器進行總擾動估計并給予補償。

2.1 旋轉運動子系統控制

根據式(13)，在考慮擾動的情況下，四旋翼無人直升機的旋轉運動方程為

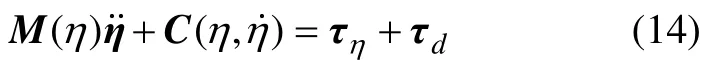
定義跟蹤誤差：

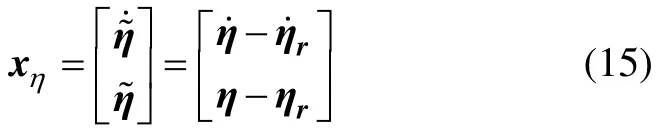
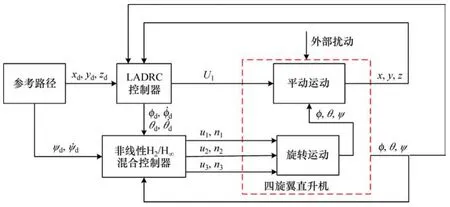
圖2 控制結構Fig.2 Control structure

定義T矩陣形式如下：

其中：T11=aI3×3,T12=bI3×3；a和b為待定正數；O和I分別為3階零矩陣和單位矩陣。

由式(14)和式(15)可以推導出基于誤差的狀態空間表達式：

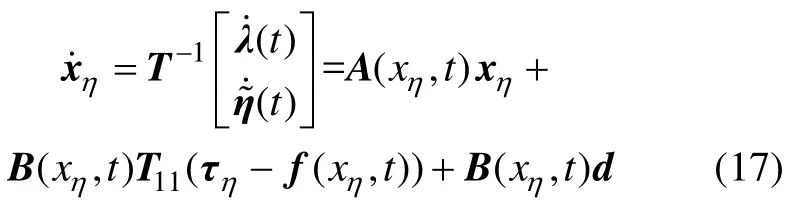
其中：

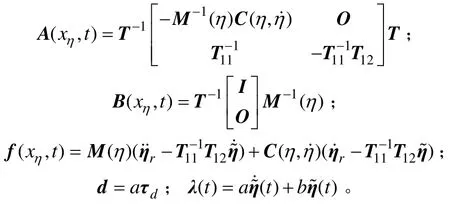
對于該旋轉子系統，可設計如下控制律：

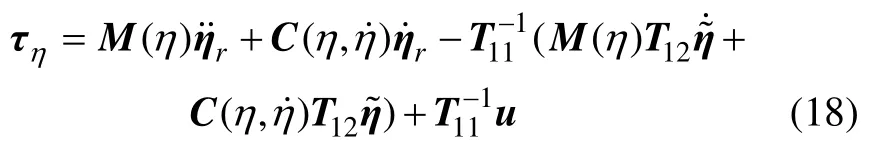
則基于狀態誤差的四旋翼直升機旋轉運動方程可以重新表達為

其中：u為控制輸入；n為外部擾動。

對于具有參數不確定和外部擾動的四旋翼旋轉運動系統，在有權矩陣Q1，Q1f，Q2，Q2f，R1，R2和P全部為對稱正定矩陣，γ+∈R 的條件下，若控制器能在H∞擾動估計最大范圍內，

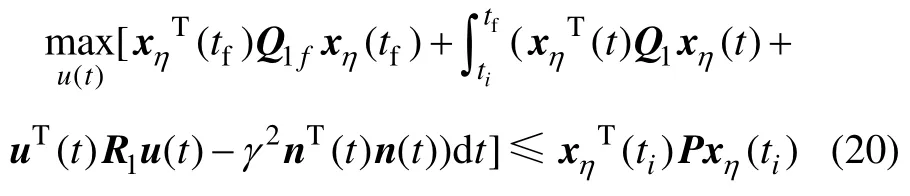
滿足H2最優跟蹤控制

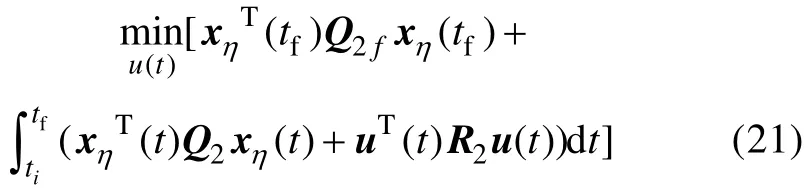
則可設計H2/H∞混合控制器，實現其穩定控制(其中，ti和tf表示控制的初始和最終時刻)。定義2個性能指標如下：

即需要滿足的條件為

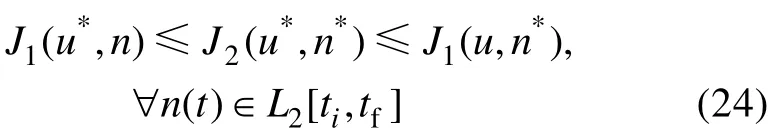
其中：u*和n*分別代表最優控制輸入和最壞的擾動情形。

定理1[23]：對于式(19)中的誤差狀態系統，最優控制和最壞擾動可以分別選擇以下形式：

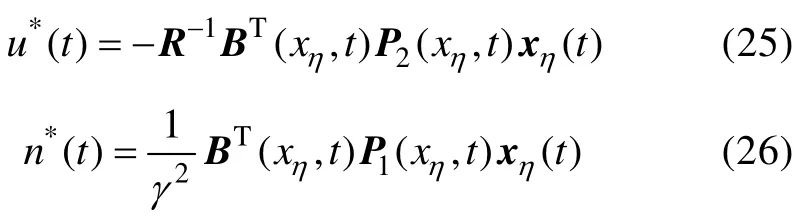
其中：P1(xη,t)和P2(xη,t)為耦合非線性時變Riccati形式方程的解，具體形式參考文獻[23]。

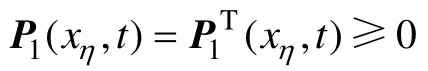
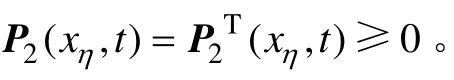
若選擇P1(xη(tf),tf)=Q1f和P2(xη(tf),tf)=Q2f，代入式(25)和(26)，則式(25)和(26)就成為式(24)中H2/H∞混合控制最優跟蹤問題的解。

定理2：若R1，R2和R定義為

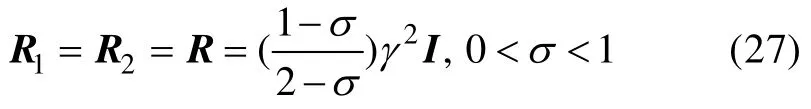
選取Q1和Q2為

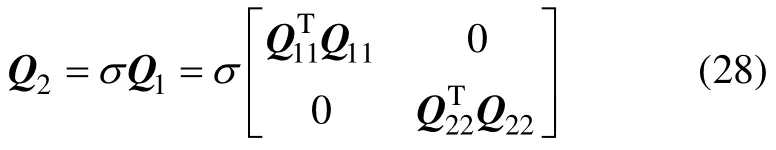
其中：Q11=q11I；Q22=q22I；q11＞0；q22＞0。

非線性時變Riccati形式方程解為

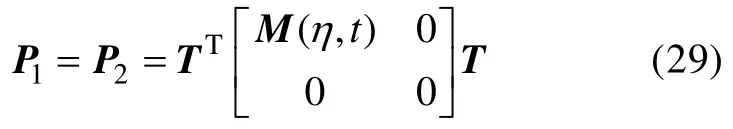
轉換矩陣T選擇如下形式：

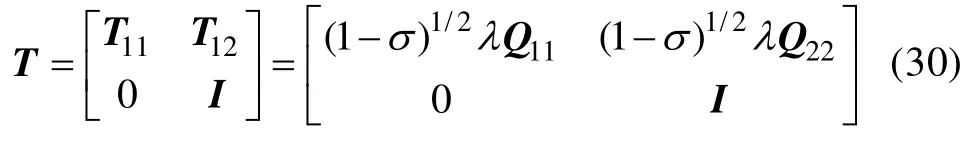
參數a和b分別為：

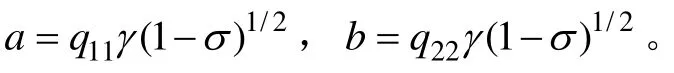
2.2 平移運動子系統控制

其 中 ：uz=cosφcosθ,ux=cosψsinθcosφ+sinψsinφ,uy=sinψsinθ- cosψsinφ。

2.2.1 高度控制

以高度控制為例，設計自抗擾控制器，使得輸出能夠快速穩定跟蹤設定值。考慮高度系統如下：

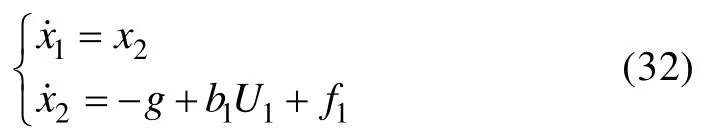
令x3=f1作為高度通道的擴張狀態，且其導數為h1，則式(32)所示系統可以擴張為

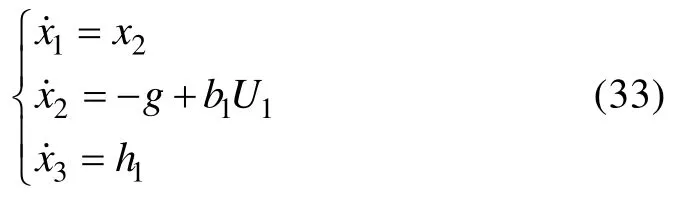
其中：x1=z表示高度；U1為控制輸入。

式(33)對應的擴張狀態觀測器設計為

其中：zi(i=1，2，3)為狀態xi(i=1，2，3)的估計值；βi(i=1，2，3)為觀測器增益，為可調參數，且，；ωo1為觀測器帶寬。

控制律及補償部分為：

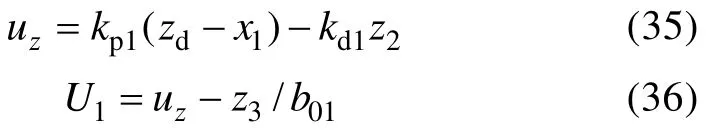
2.2.2 橫縱向運動控制

對于四旋翼的縱向運動和橫向運動，設計線性自抗擾控制器時，設計控制律u0i(i=1，2)，補償總擾動后，獲得相應通道和擴張狀態觀測器的控制輸入，ux，uy分別表示縱向運動和橫向運動通道的虛擬控制律，與姿態角設定值θd和φd的關系為

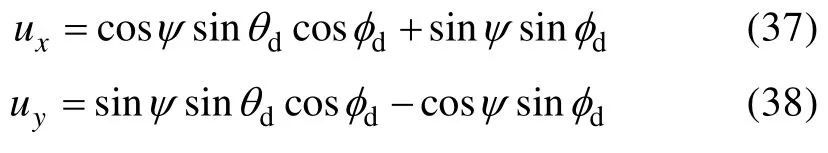
四旋翼的縱向運動的狀態空間表達式為

令x6=f2作為縱向運動通道的擴張狀態，且其導數為h2，則式(39)所示系統可以擴張為

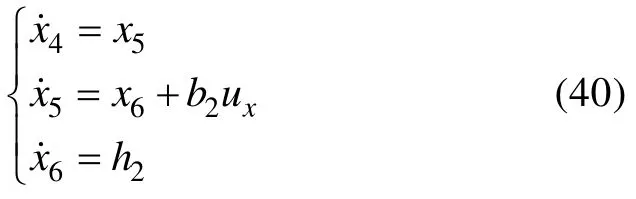
式(40)對應的擴張狀態觀測器可設計為

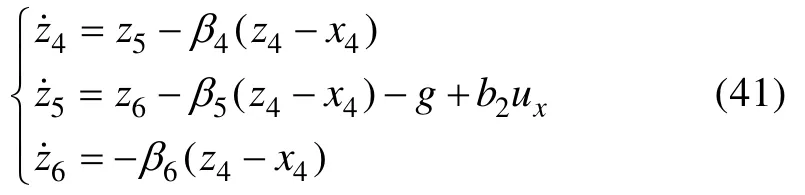
其中：zi(i=4，5，6)是狀態xi(i=4，5，6)的估計值；βi(i=4，5，6)為觀測器增益，為可調參數，且；ωo2為觀測器帶寬。

相對應的控制律可以選擇為

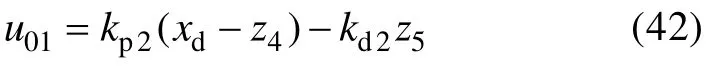
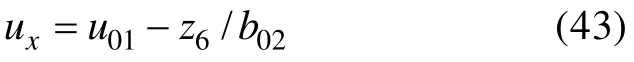
對于飛行器的橫向運動，其狀態空間表達式為

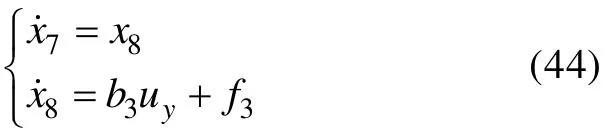
同理，可得如下四旋翼無人飛行器橫向運動的控制器設計：

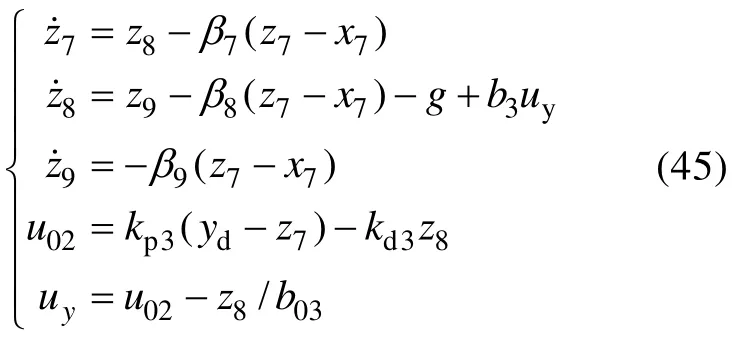
其中：zi(i=7，8，9)為橫向通道狀態及總擾動的估計值；βi(i=7，8，9)為觀測器增益；b03為可調參數；；ωo3為觀測器帶寬；u02為誤差控制律，控制器增益；ωc3為控制器帶寬；yd為側向移動設定值。

3 仿真結果

仿真中，選取四旋翼無人直升機的物理參數為機體質量m=2.85 kg，槳距l=0.197 m，x，y和z軸轉動慣量分別為Ixx=Iyy=0.055 2 kg·m2和，重力加速度g=9.81 m/s2。參考路徑設定為：x坐標變化設定值，y坐標變化設定值，z坐標變化設定值，偏航角設定值；飛行器的初始位置設定為(x，y，z)=(0，0，0)m，初始姿態角設定為(φ，θ，ψ)=(0，0，0)rad。在位置和姿態輸出通道中分別添加白噪聲擾動，功率為10-7。在仿真過程中，考慮參數的不確定性，對慣性參數上下浮動20%后，進行仿真并比較結果。其中，非線性混合H2/H∞控制器參數被整定為：γ=1，σ=0.5，q22=1；LADRC 控制器參數整定為：b01=1，b02=0.9，b03=0.9，ωo1=40，ωc1=150，ωo2=10，ωc2=5，ωo3=10，ωc3=5。

白噪聲擾動下路徑跟蹤效果如圖3所示。四旋翼直升機從初始位置(x，y，z)=(0，0，0)m開始，沿設定路徑進行飛行，參考路徑起點為(x，y，z)=(0，0，1)m，利用持續的白噪聲信號干擾來模擬實際飛行產生的測量誤差和外部干擾等因素，因此，在仿真結果中，系統輸出存在不同程度的波動。從圖3可以看出：四旋翼直升機軌跡能夠較好地在較短時間內到達預期設定值，并較好地按照預設路線飛行；在對標稱慣性參數進行20%上下浮動時，飛行軌跡沒有發生較大變化，說明系統具有較強的魯棒性。

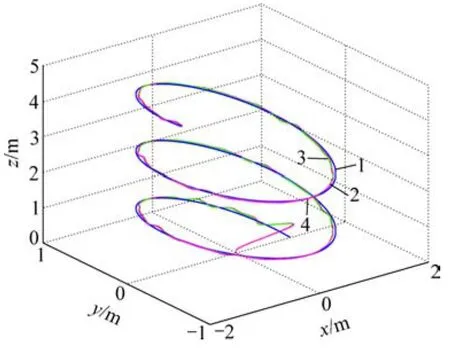
圖3 白噪聲擾動下路徑跟蹤效果Fig.3 Path tracking under white noise disturbance

圖4 白噪聲擾動下位置坐標變化Fig.4 Position coordinates under white noise disturbance

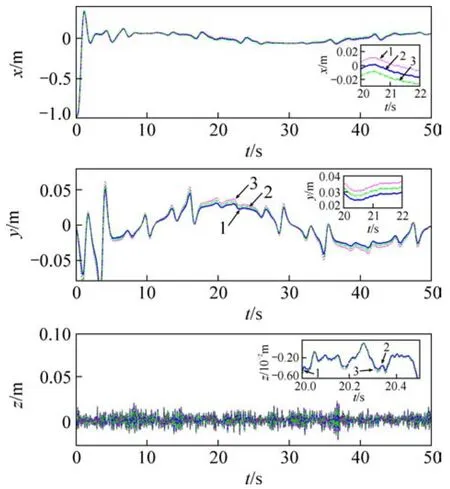
圖5 白噪聲擾動下位置跟蹤誤差Fig.5 Attitude angle tracking error under white noise disturbance

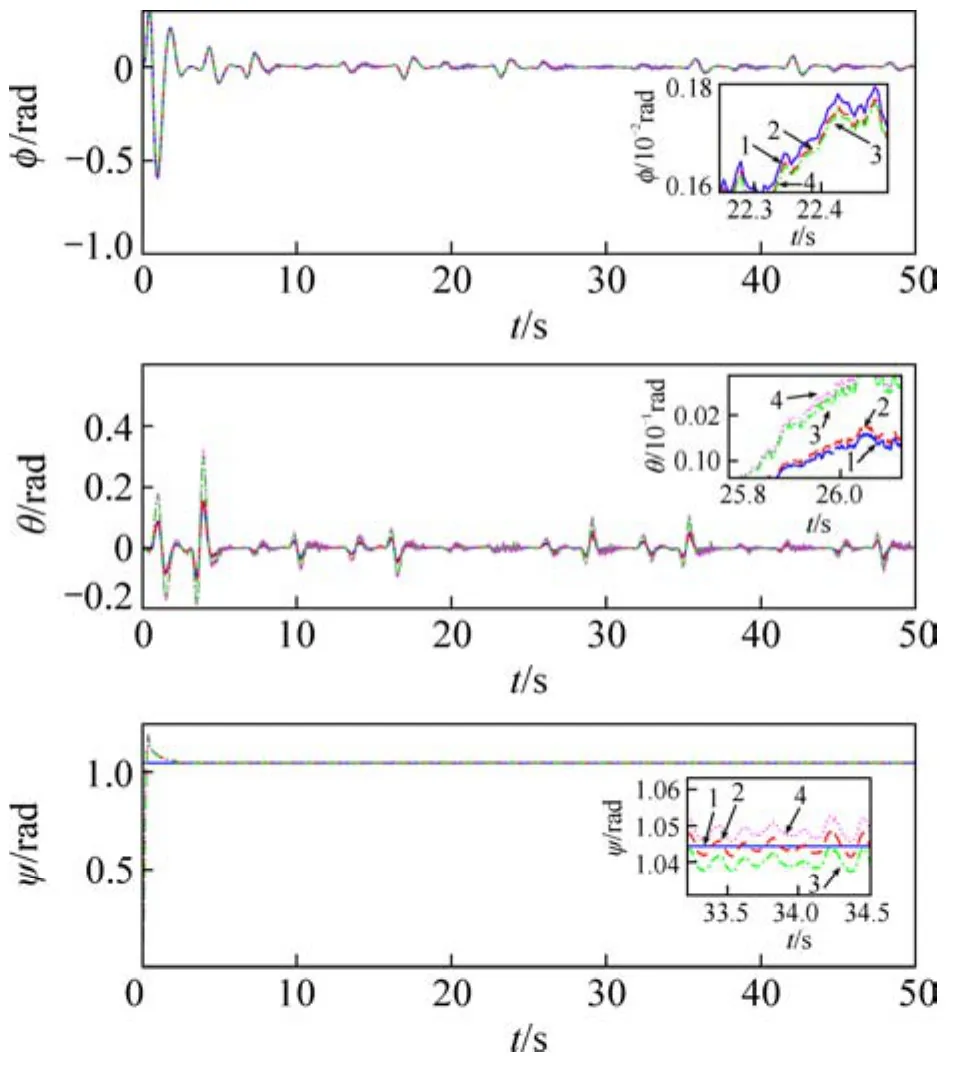
圖6 白噪聲擾動下姿態角變化Fig.6 Attitude angle under white noise disturbance

四旋翼直升機在運動中位置坐標x，y和z的變化過程見圖4。坐標x在大約2 s能夠迅速跟上設定值，響應速度較快，y和z均能較好地穩定跟蹤預設值。白噪聲擾動下位置跟蹤誤差見圖5。從圖5可以看出：對模型中標稱慣性參數進行20%上下浮動，控制器參數保持不變，系統輸出依然能夠保持較小的跟蹤誤差，說明所采用的控制器對四旋翼直升機的參數不確定性具有較強的魯棒性。圖6所示為四旋翼直升機旋轉運動中各姿態角的變化情況。從圖6可見：在自噪聲干擾下，滾轉角φ和俯仰角θ能夠較平穩地變化；偏航角ψ在大約2 s達到設定值，盡管產生一定的超調量，但能夠迅速到達穩定設定值并保持不變，在慣性參數進行±20%變化時，仍然可以保持較好的控制效果。

4 結論

1)針對四旋翼直升機的軌跡跟蹤問題，設計了一種線性自抗擾與非線性 H2/H∞混合控制結合的控制策略。首先，基于拉格朗日-歐拉方程獲得四旋翼直升機的強非線性數學模型。在此基礎上，將位置系統中的未知擾動作為系統的擴張狀態，并設計相應的線性自抗擾控制器；針對姿態的穩定跟蹤控制問題，采用了一種非線性 H2/H∞混合控制方法，能夠使外擾衰減的同時保持良好的H2跟蹤性能。

2)本文所設計的四旋翼直升機穩定控制算法能夠較好地抑制系統參數不確定性和外部擾動的影響，具有響應速度快、魯棒性強等優點。