裝配式UHPC防船撞耗能裝置的性能

周凌宇，濮星旭，衛軍

(中南大學 土木工程學院，湖南 長沙，410075)

自20世紀80年代起，我國在寬闊水域、外海深水環境下建設的橋梁日益增多，在促進我國交通事業高速發展的同時也加劇了船橋碰撞風險。據統計，我國僅武漢、南京、枝城、九江4座長江大橋迄今已發生船撞事故 100余次[1]。一旦發生船撞橋事故，橋梁結構需要承受巨大的側向沖擊荷載，設計時，必須對船撞問題予以充分考慮，否則，可能導致橋梁結構發生嚴重破壞甚至完全倒塌，造成巨大的經濟損失、人員傷亡以及消極負面的社會影響。改善橋梁結構防撞性能的重要途徑之一是設置被動式防撞裝置。由于防撞裝置的材料及結構形式種類眾多，其各自的防護特點與適用范圍也有所不同[2-4]。目前，國內運用最廣泛的防撞裝置是在防撞范圍、船舶損傷程度、經濟性等方面都具有較明顯優勢的鋼結構護舷，而防撞等級與其相當、經濟性和耐久性更好的混凝土結構護舷由于撞損修復較困難、大塑性變形結構耗能難以準確把握等，沒有受到國內外工程人員的重視。但鋼材本身易腐蝕，使得鋼結構護舷在橋梁服役年限內維修成本較高，因此，研發一種兼顧鋼結構護舷優點、克服普通混凝土易損的缺陷且耐久性好的新型防撞裝置十分必要。鑒于超高性能混凝土(簡稱 UHPC)材料強度高、韌性好及耐久性優異，研發設計能抵擋中等能量撞擊而微損傷的一種經久耐用的裝配式UHPC防船撞耗能裝置很有必要。目前，超高性能混凝土材料配合比設計已趨于成熟，且已在多個工程中得到應用，其中以在橋梁方面應用最多。據不完全統計，全世界以UHPC作為主結構修建的橋梁有30多座，如加拿大舍布魯克人行橋、韓國仙游人行拱橋、日本酒田未來步行橋和GSE公路橋、奧地利威爾德公路拱橋、廣東馬房橋、長沙北辰三角洲橫四路跨街天橋等[5-6]。若將 UHPC材料用于防船撞耗能裝置，則同樣可以獲得很好的防撞效果。分離式Hopkinson壓桿技術被認為是測量固體材料在 10～103s-1應變速率下動態特性最有效的方法。為了研究超高性能混凝土在國防工程中的抗壓強度，RONG等[7]制備了抗壓強度為200 MPa的超高性能混凝土，并采用Hopkinson壓桿研究了不同纖維摻量下UHPC的抗壓強度，發現UHPC的抗沖擊性能、抗壓強度以及抗彎強度隨著纖維摻量的增大而增大，也隨應變率的增大而增大。也就是說，UHPC在動態作用下所能承受的應力會遠大于其在準靜態試驗中得出的抗壓強度。不同強度等級的UHPC在不同應變率下(100～250 s-1)的強度可增大60%～130%。為此，本文作者對一種裝配式UHPC高性能防船撞耗能裝置的防撞性能進行評估，依托工程實例采用 ANSYS/LSDYNA程序模擬船舶撞擊該新型防撞裝置，對最大撞擊力、撞擊持續時間和能量耗散特性等進行分析和對比。

1 項目概況

新型防撞裝置的工程應用背景為珠海市洪鶴大橋，該橋為一橫跨洪灣水道與磨刀門水道的斜拉橋。根據工程建設時的船撞研究成果，選用9號橋墩作為本文計算實例(見圖1)。索塔高為162.6 m，承臺頂面標高為-5.5 m，基礎采用24根直徑為2.8 m的鉆孔灌注樁。防撞浮箱由76個預制獨立的UHPC分箱組成雙層高性能防船撞耗能裝置，可以隨水位變化而上下自由浮動，結構形式見圖2。該防撞浮箱采用帶有分水尖的平面形式，這種形式可以卸掉船撞時部分附連水質量并撥轉船頭以改變撞擊方向，必要時可在浮箱外壁安裝1圈滾筒。其立面形式為矩形截面的整體結構，高為6.0 m。各箱體結構采用模塊化生產，壁厚為4.0 cm，混凝土保護層厚度為10.0 mm，配備直徑為10.0 mm的HRB400E鋼筋。防撞浮箱外壁板采用密配筋，配筋率約為6.0%；內隔板采用疏配筋，配筋率約為3.5%。浮箱由高強螺栓進行連接并用石棉墊板填充箱體之間縫隙，以防止箱體之間硬接觸而出現損傷。防撞浮箱的箱體空腔體積占比大，能給整體結構提供足夠的浮力，且結構形式對稱，保證了結構中心與浮心重合。為了避免防撞浮箱和橋墩硬接觸而出現損傷，在防撞浮箱內壁安裝1層橡膠阻尼材料。根據橋梁圖紙、設計說明等相關資料提供的通航水位，取防撞高水位為2.944 m。

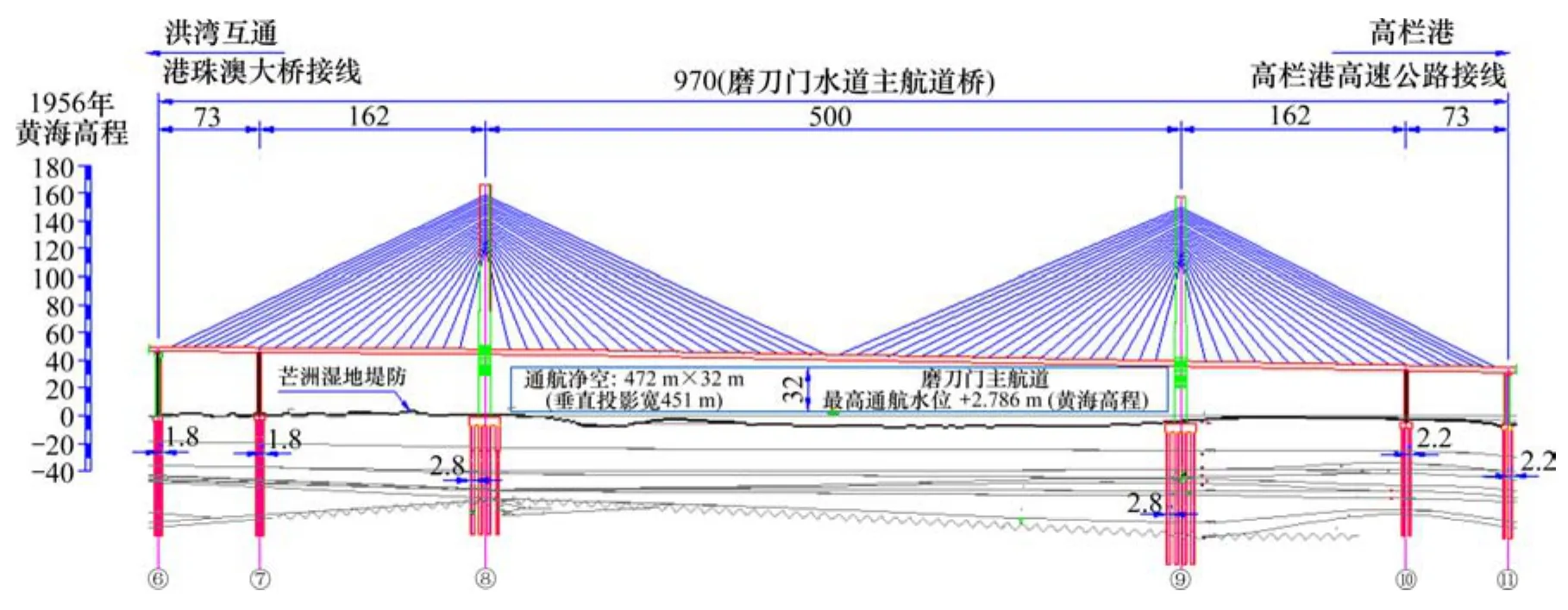
圖1 洪鶴大橋磨刀門水道橋跨布置圖Fig.1 Elevation view of Modaomen channel structure of HongHe bridge

圖2 橋墩UHPC防船撞裝置Fig.2 UHPC fender system designed for protected bridge pier

檢驗新型防撞裝置性能最合理的辦法是進行實橋船撞試驗，但這種試驗實施困難且試驗費用較高，其試驗結果也具有一定程度的偶然性，而采用縮尺模型試驗又會忽略結構尺寸效應所帶來的影響，目前多采用數值模擬的方法研究此問題，并且經一系列結構沖擊試驗和計算校準研究證明，數值模擬結果具有較高的可信度[8]。

2 新型防船撞耗能裝置數值模擬

2.1 橋墩有限元模型

橋墩承臺、塔身及樁基礎均采用 ANSYS/LSDYNA程序中實體單元SOLID164建立，單元尺寸按長和寬均為0.5 m進行劃分，共382 597個單元，且單元采用單點高斯積分并進行沙漏控制。橋墩有限元模型見圖3。

圖3 橋墩有限元模型Fig.3 FE Model of bridge pier

樁基礎建模長度與實際長度相等，約束樁底單元節點三向平動自由度。

為了提高程序計算效率，橋墩碰撞區域以上混凝土材料采用剛體建模，取密度ρ=2 500 kg/m3，彈性模量E=3.45×104MPa，泊松比μ=0.2。其余部分橋墩混凝土材料模型采用 Colorado 帽蓋模型，通過1個由失效包絡面、硬化端帽蓋面和拉力切斷極限面組成的失效面表達，能較好地反映材料大應變時的非彈性響應，其具體參數取值見表1[9]。

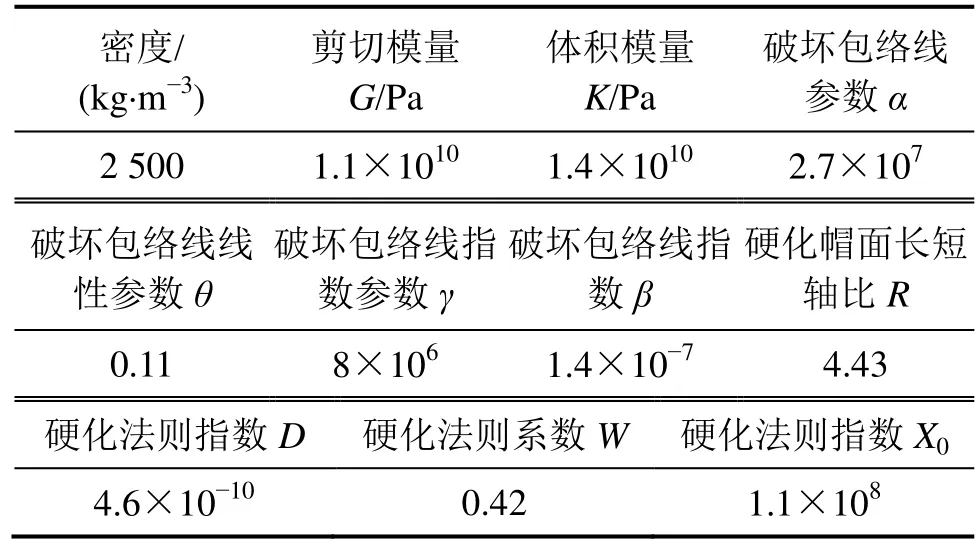
表1 混凝土材料模型參數Table 1 Material properties of bridge pier

2.2 防撞浮箱有限元模型

防撞浮箱根據設計用四節點殼單元SHELL163進行精細化建模，共 13 656個單元。程序采用Belytschko-Tsay單點積分的殼單元算法并進行黏性沙漏控制。該算法在處理大應變問題中與全積分單元算法相比具有更高的精度。由于超高性能混凝土中橫向、縱向和垂直方向上的纖維布局不均勻，其彈性模量和強度具有正交性，所以，防撞浮箱采用正交各向異性彈性模型即*MAT_ORTHOTROPIC_ELASTIC模型。該模型用于大規模非線性分析時計算效率較高。具體參數值為：密度ρ=2 600 kg/m3，彈性模量E=5×104MPa，剪切模量G=3 GPa，泊松比μ=0.2。為了考慮模擬過程中材料的破壞，添加關鍵字*MAT_ADD_EROSION刪除變形過大或者畸形的單元[10]。根據 UHPC 材料的力學性能，取最大失效主應變為0.02，最大失效剪切應變為0.70。另外，防撞浮箱與內側橡膠簡化為共節點連接，橡膠本構模型采用*MAT_MOONEYRIVLIN_RUBBER 模型[11]。取密度ρ=1 600 kg/m3，泊松比μ= 0.499 5，參數C10和C01為該模型的材料常數，C10=0.60 MPa，C01=0.15 MPa。

2.3 船舶有限元模型

根據船撞統計結果，選用5000DWT江海直達貨船(總排水量6 845 t，總長110 m，型寬17.5 m，型深7.6 m，設計吃水4.5 m)作為本文計算代表性船舶，并考慮航速為1，3和5 m/s共3種撞擊速度工況。船舶有限元模型由船首和船身2部分組成，見圖4。船橋碰撞是一個非線性碰撞過程，在船舶與橋墩發生碰撞過程中，船首結構會出現屈曲、壓潰等破壞現象，因此，必須準確模擬船首的形狀和結構(包括外板、各層甲板及橫向艙壁等主要構件)才能得到可靠的船橋碰撞過程[12]。為了保證計算結果的準確性，更加真實地模擬碰撞過程中鋼板的彈塑性變形與失效，船首網格采用殼單元SHELL163細化處理，共計9 630個單元。另外，建立長度為86 m的船身有限元模型以反映船舶的實際長度；同時，為了減少結構自由度數，提高程序計算效率，在劃分船身有限元網格時，其單元尺寸相對較大[13]，共計1 2647個SHELL163殼單元。

考慮船首鋼材應變率效應，其外板、甲板及橫向艙壁采用塑性隨動硬化模型即*MAT_PLASTIC_KINEMATIC模型，并用Cowper-Symonds本構方程來描述船首鋼材的黏塑性行為[14]，屈服應力yσ表示為

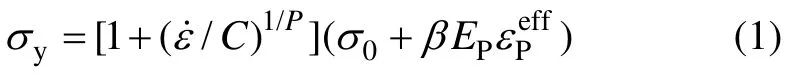
式中：σ0為初始屈服應力；ε˙為應變率；C和P為Cowper-Symonds應變率參數；β為硬化參數；為有效塑性應變；EP為塑性硬化模量，

本文采用具體參數值為：密度ρ=7 850 kg/m3，彈性模量E=2.1×105MPa，硬化模量Etan=1.18×103MPa，靜屈服應力σ0=2.35×102MPa，由于船首材料為低碳鋼，所以，取泊松比μ=0.3，硬化參數β=0，失效應變εf=0.34。由于船首材料為低碳鋼，所以，取參數C=40.4，P=5。

流固耦合模型的數值仿真將造成 CPU運行時間急劇增大，因此，本文取附加質量為船體總質量的4%來模擬流體對船舶的影響，通過等效密度法實現[15]。

由于船體中后部遠離撞擊區域，不會產生塑性變形或屈曲，因此，船身可采用剛體建模，并改變其密度以模擬真實船體質量。改變密度對計算結果影響很小，但計算效率顯著提高[16]。

2.4 接觸定義

為準確模擬船橋碰撞過程，在船首與防撞浮箱之間定義接觸算法*CONTACT_AUTO-MATIC_SURFACE_TO_SURFACE，其動、靜摩擦因數均取0.2，并在防撞浮箱與橋墩及船首與橋墩之間定義同樣的接觸算法，其動、靜摩擦因素均取0.3。由于船橋碰撞屬于大變形問題，在碰撞過程中可能會造成船首鋼材和防撞浮箱自身的相互接觸，因此，采用動、靜摩擦因數均為0.2的接觸算法*CONTACT_AUTOMA-TIC_SINGLE_SURFACE，以檢測碰撞過程中發生的所有接觸。

圖4 船舶結構圖Fig.4 Structure of ship

3 碰撞結果分析

3.1 5 m/s撞擊速度下無防撞裝置的船橋碰撞

在一般情況下，船橋正面碰撞為最不利工況，往往會對橋墩造成嚴重的損害，因此，本文就船橋正撞情況下的最大撞擊力和能量耗散特性等問題展開研究與分析，并采用撞擊速度5 m/s進行計算。無防撞裝置的正撞有限元模型見圖5。從圖5可以看出：船首鋼材出現了屈曲、壓潰及應力集中等現象，破壞較嚴重。

無防撞裝置情況下的數值模擬結果見圖6。在圖6(a)中，船橋x方向(即船舶航行方向)的撞擊力在碰撞發生后的0.72 s達到最大值31.1 MN，然后迅速下降為0 MN，撞擊持續時間為1.35 s。由于船舶沒有沿y方向的速度分量，所以，船橋y方向撞擊力基本接近于0 MN，而橋墩側面與水平面不垂直，其z方向撞擊力峰值分別為-1.75 MN和1.86 MN。圖6(b)所示為船橋碰撞過程中的能量轉換情況，系統總能量為任意時刻結構體系的動能、內能、沙漏能及滑移能之和。船舶初始動能為90.09 MJ，在船橋碰撞發生后，船舶動能迅速減少并轉換為船首與橋墩的變形能和內能。船舶動能在1.35 s后減少97.41%，這會給船首及橋墩帶來嚴重損害。另外，船舶與橋墩之間的最大滑移能為9.51 MJ，占船舶初始動能的 10.56%，而沙漏能最大值為3.55 MJ，遠低于系統內能，這表明數值模擬結果是可靠的。

3.2 5 m/s撞擊速度下有防撞裝置的船橋碰撞

有防撞裝置的正撞有限元模型見圖7。防撞浮箱與橋墩碰撞開始于0.40 s，并在1.68 s時達到最大變形。其大變形提供的柔性保護有效防止了船首及橋墩的嚴重破壞，而防撞浮箱的破壞僅局限于碰撞接觸區域。

有防撞裝置情況下的數值模擬結果見圖8，其中，圖8(a)所示為有/無防撞裝置情況下沿船舶航行方向的撞擊力隨時間的變化情況。從圖8(a)可見：有防撞裝置情況下的最大撞擊力為20.79 MN，比無防撞裝置情況下的最大撞擊力31.10 MN低33.15%；其碰撞持續時間大約為3.63 s，比無防撞裝置情況下的碰撞持續時間1.35 s多168.89%，因此，有防撞裝置時，最大撞擊力顯著減小，撞擊持續時間顯著延長；另外，防撞裝置在碰撞過程中所承受的局部最大等效應力約為613 MPa，大幅度超過UHPC材料強度，使得撞擊力時程曲線出現明顯震蕩現象。這是由于防撞浮箱在撞擊壓潰過程中產生了局部的結構失效與應力重組，待船舶動能大部分轉化為浮箱變形能后，其承受的撞擊等效應力逐漸減小至低于UHPC材料強度，從而對橋墩和船舶均起到了很好的緩沖消能效果。

圖5 無防撞裝置的正撞有限元模型Fig.5 FE model of head-on collision without fender system

圖6 無防撞裝置的正撞數值模擬結果Fig.6 Simulation results of head-on collision without fender system

圖7 有防撞裝置的正撞有限元模型Fig.7 FE Model of head-on collision with fender system

圖8(b)所示為有防撞裝置情況下的能量轉換情況。從圖8(b)可見：船舶初始動能為90.09 MJ，并在0.15 s后迅速減少，約有87.76 MJ轉換為其他形式的能量；船舶動能在碰撞發生后2.98 s減少了97.41%，比無防撞裝置情況下船舶動能轉換為內能所需的1.35 s多 120.74%；在有防撞裝置時，最大內能為60.75 MJ，比無防撞裝置時的最大內能75.93 MJ下降19.99%，這表明UHPC防撞浮箱有很好的緩沖性能和能量耗散能力；此外，約有16.84%的船舶初始動能轉換為船舶、防撞裝置及橋墩之間的滑移能，而沙漏能最大值僅為5.49 MJ，占系統內能的9.04%，這表明數值模擬精度較高。從系統各部件的能量轉換來看，無防撞裝置情況下船首所承受的最大內能為61.07 MJ，而防撞裝置的存在使得船首承受的最大內能下降到47.68 MJ(下降21.93%)，有效減少了船首的局部損傷變形。同樣，無防撞裝置情況下橋墩所分擔的動能與內能之和為9.66 MJ，而防撞裝置的存在使得橋墩分擔的動能與內能之和下降到3.80 MJ(下降60.66%)，說明這種防撞裝置具有非常強的吸能能力，可對橋墩起到很好的保護作用。在系統各部件能量轉換過程中，防撞浮箱、橡膠阻尼材料、橋墩三者耗能能量之比為4.02:0.13:1.00，進一步表明防撞裝置對提高橋梁結構的安全系數具有重要意義，而橡膠阻尼材料耗能比例雖然較小，但可以防止浮箱與橋墩硬接觸而出現局部損傷。

圖8 有防撞裝置的正撞數值模擬結果Fig.8 Simulation results of head-on collision with fender system

表2 由不同規范計算的撞擊力Table 2 Impact force obtained by different standards

3.3 不同撞擊速度下的正撞結果分析

圖9所示為不同撞擊速度下有/無防撞裝置的撞擊力時程曲線。從圖9可見：在無防撞裝置情況下，撞擊速度為1，3和5 m/s對應的最大撞擊力分別為6.42，16.57和31.10 MN；與有防撞裝置時相比，其對應的最大撞擊力則分別為5.20，10.08和20.79 MN，見表2。可見，防撞裝置的存在使最大撞擊力分別降低了19.00%，39.17%和33.15%。

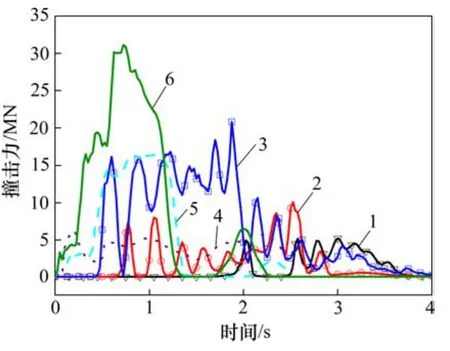
圖9 不同撞擊速度下的正撞數值模擬結果Fig.9 Simulation results of head-on collision under different impact velocities

在數值模擬基礎上，通過“公路橋涵設計通用規范”[17]、“鐵路橋涵設計規范”[18]、AASHTO[2]及Eurocode[19]中提供的船撞力計算經驗公式，對各經驗公式的計算數值與數值模擬結果進行比較，結果見表2。

從表2可以看出，依據“鐵路橋涵設計規范”計算的撞擊力最小，其次是“公路橋涵設計通用規范”和AASHTO，而依據Eurocode計算出的撞擊力最大。在1，3和5 m/s這3種不同撞擊速度下，無防撞裝置的數值模擬結果與基于“公路橋涵設計通用規范”計算的撞擊力偏差分別為8%，21%和11%，與基于“鐵路橋涵設計規范”計算的撞擊力偏差分別為 83%，57%和76%，與基于AASHTO計算的撞擊力偏差分別為24%，35%和27%，與基于Eurocode計算的撞擊力偏差分別為37%，45%和39%。由于“鐵路橋涵設計規范”中規定的動能折減系數γ偏小，且彈性變形系數C1和C2難以掌握，最終導致偏差較大。結果表明：基于“公路橋涵設計通用規范”計算的撞擊力與數值模擬結果較吻合。

根據珠海市洪鶴大橋橋墩防撞標準，9號橋墩可以承受的最大撞擊力約為27.2 MN。由表2可知：當撞擊速度為1 m/s和3 m/s時，無防撞裝置情況下的最大撞擊力均低于橋墩設計抗力，防撞裝置的存在可以提高橋梁安全系數，并能防止橋墩混凝土局部破壞和船首過大變形；當撞擊速度為5 m/s時，無防撞裝置情況下的最大撞擊力為31.10 MN，顯然已經超過橋墩設計抗力27.20 MN，危及橋梁安全。然而，防撞裝置的存在使最大撞擊力下降到非破壞性水平20.79 MN，有效保護了橋梁結構。需說明的是：撞擊力數值模擬結果與現有文獻[10,12-16]中的結果處于同一數量級，反映了所得結論的合理性。

4 結論

1)新型防撞裝置由模塊化生產的獨立 UHPC分箱組成。各分箱通過高強螺栓進行連接，采用的預制拼裝技術具備預制用地少、施工速度快、控制精度高和橋下交通影響小等特點。該防撞裝置可以顯著減小峰值撞擊力和延長撞擊持續時間，在1，3和5 m/s這3種不同撞擊速度下，最大撞擊力分別降低19.00%，39.17%和 33.15%，撞擊持續時間分別延長 47.68%，132.61%和168.89%。

2)新型防撞裝置具有非常強的吸能能力，對橋墩和船舶均起到了很好的保護作用，兩者損傷變形較小，而防撞裝置本身的損傷變形主要集中于碰撞接觸區域。新型防撞裝置具有強度高、韌性好、生產模塊化、現場安裝高效、隨水位自由浮動、耐腐蝕性能優異、維護成本低以及更換方便等優點。

3)超高性能混凝土的優異性能決定了新型防撞裝置較好的防撞耗能能力。該新型防撞裝置可以有效提高橋梁結構安全系數。