裂隙對含孔洞砂巖力學及損傷演化特征的影響

周軍華，楊坤，房凱，趙同彬，邱東衛

(1.山東科技大學 礦山災害預防控制省部共建國家重點實驗室培育基地，山東 青島,266590;2.山東科技大學 礦業與安全工程學院，山東 青島,266590)

巖體內部存在的不同幾何形態裂隙或孔洞等缺陷，使得巖體的結構和力學特征復雜，造成巖體被破壞與失穩。不同類型的缺陷之間相互作用對巖體力學及損傷演化特征有重要影響，對含孔洞巖體而言，周邊裂隙的存在影響著巖體的力學及損傷演化特征，進而影響巖體的工程特性，因而系統研究裂隙對含孔洞砂巖力學機制、裂紋擴展特征的影響，分析2種缺陷同時存在條件下巖體內部裂紋的損傷演化特征，對于巖石工程的穩定性分析具有重大意義。目前，國內外許多學者對缺陷巖體的力學及損傷演化特征進行了大量研究[1–4]。LEE 等[5–6]對預制裂隙的巖體進行單軸壓縮試驗，分析了缺陷幾何對巖樣強度和變形破壞特征的影響規律。LAJTAI等[7–8]研究了壓應力場下孔洞缺陷周邊的破裂演化過程。WADLEY等[9]通過大量試驗發現聲發射振鈴計數更能反映材料內部損傷的演化過程。周喻等[10]基于PFC程序，根據矩張量理論建立了細觀尺度上巖石聲發射模擬方法，結合室內巖石破裂全過程聲發射特性試驗，對比驗證了顆粒流方法研究聲發射模擬的可靠性。TANG等[11–12]建立了單軸應力狀態下巖石基于聲發射的損傷模型，得出了煤巖的損傷演化曲線和方程。LI等[13–15]的研究表明，巖體力學參數及聲發射特征顯著受孔洞裂隙等缺陷分布的影響。大量研究表明，聲發射是研究巖體失穩損傷演化過程的重要手段，砂巖變形破裂過程中的裂紋擴展及聲發射特征顯著，因此，對含孔洞砂巖的力學及損傷演化研究具有重要意義，而目前人們針對含孔洞砂巖中裂隙存在的幾何形態對其力學及損傷演化特征的影響分析較少。為此，本文作者采用顆粒流軟件PFC數值模擬構建不同裂隙幾何形態的含孔洞紅砂巖試樣模型，研究在單軸壓縮下裂隙形態對含孔洞巖樣破裂和力學特征的影響規律，并基于聲發射特征和應變等效原理，利用損傷修正系數對損傷本構模型進行修正，探討含孔洞巖樣的損傷演化規律。

1 含孔洞紅砂巖數值模型

CUNDALL等[16]在離散元法的基礎上創建了顆粒流理論，該理論適合從細觀層次上分析材料的損傷演化破斷機制及大變形過程。PFC模型的巖石能夠重現真實巖石樣本中觀察到的許多行為特征，例如應力–應變響應、開裂和破裂模式。巖石的聲發射與巖石內部微破紋的產生直接相關，PFC模型中1個鏈接斷裂會產生1次應變能的釋放，即發生了1次聲發射，通過統計顆粒鏈接斷裂數即可模擬巖石聲發射事件[17]。在模擬顆粒黏結破壞過程中，PFC程序利用設置黏結模型來表征顆粒之間膠結物的存在，本文采用平行黏結模型來對砂巖進行模擬及細觀參數的標定[18]，最終細觀物理力學參數見表1。利用表1中參數計算得巖樣顆粒流模型與室內試驗的力學特性，見表2和圖1。從表2和圖1可以看出：兩者力學特性基本一致，表明其選取較合理并可用于后續的計算分析。

表1 紅砂巖細觀物理力學參數Table 1 Physico-mechanical parameters of red sandstone

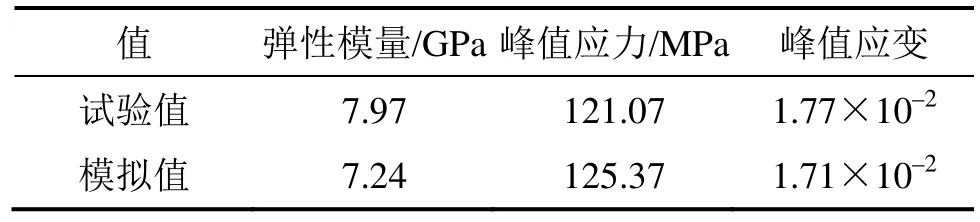
表2 完整砂巖試樣試驗和模擬力學參數對比Table 2 Comparison of mechanical parameters by test and simulation

圖1 試樣破裂模式對比Fig.1 Comparison of sample fracture mode

為了分析裂隙幾何形態對含孔洞砂巖力學特征和損傷破壞聲發射特征規律的影響，建立了同室內標準巖石尺寸一致(直徑×長度為50 mm×100 mm)的完整巖石模型，共生成1 0773個顆粒。通過預制直徑d為10 mm、圓心偏離試樣中心下10 mm的孔洞，和長度為2a、寬度為2 mm、傾角為α、中心點距孔洞距離為h的裂隙，來構建含孔洞砂巖試樣模型見圖2，圖中σ1為軸向加載。模擬11種工況，見表3。模擬加載過程采用位移加載方式，加載速率為0.05 m/s。

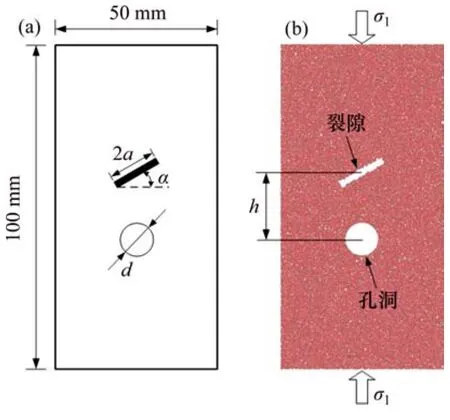
圖2 試樣孔洞裂隙參數分布Fig.2 Geometric of hole and fissure in sample

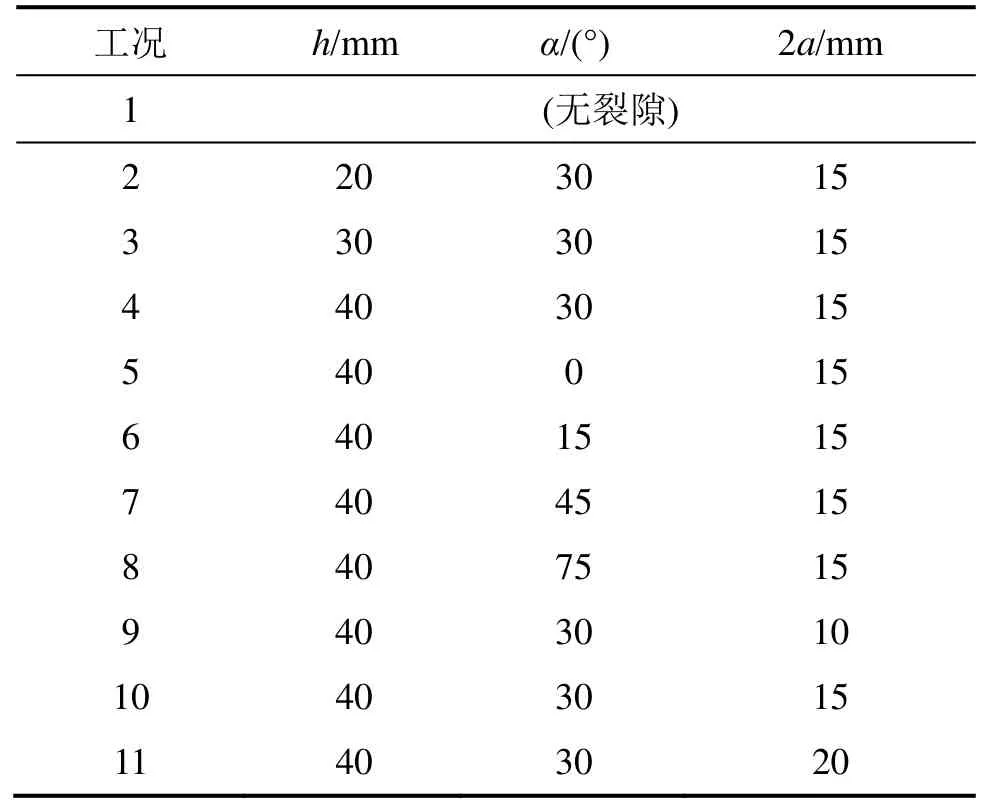
表3 模擬試驗工況Table 3 Simulation test conditions

2 試驗結果及分析

2.1 砂巖試樣破裂特征

圖3所示為單軸壓縮下不同裂隙距孔洞距離h含孔洞紅砂巖試樣的破裂模式。圖3中數字N表示為主貫裂帶裂紋的擴展順序，數字N#表示為非主裂紋的擴展順序。由圖3可知：裂隙的存在會改變原有含孔洞試樣的裂紋擴展和破裂特征。無裂隙巖樣，在孔洞上下邊緣萌生初始裂紋1和1#，繼續加載新生裂紋2萌生并迅速擴展，最終與裂紋1貫通破裂。在相同裂隙長度下，裂隙距孔洞距離h=20 mm巖樣為裂隙尖端萌生出的翼裂紋1與傾斜次生裂紋2，和共面次生裂紋3與4交叉貫通破裂；h=30 mm巖樣由裂隙尖端萌生出共面次生裂紋1與2擴展貫通破裂；h=40 mm的含孔洞巖樣，在裂隙尖端萌生出翼裂紋1與傾斜次生裂紋2，該裂紋與預制裂隙相垂直，隨后裂紋迅速擴展貫通破裂。含孔洞巖樣在破裂過程中預制裂隙與孔洞之間的微裂紋N#的擴展對巖樣的破壞并未起到關鍵作用，這意味著裂隙的存在會改變原有含孔洞試樣沿孔洞貫通破壞的破壞模式，大多數試樣會形成貫通裂隙的主破裂帶。

圖4所示為不同裂隙傾角α砂巖試樣的破裂模式。由圖4可知：隨著傾角α的增大，巖樣的破裂模式變化可分為2類，即α為0°，15°和45°巖樣為裂隙尖端發育的翼裂紋與傾斜次生裂紋貫通破裂，以及α=75°巖樣為預制裂隙左側產生的遠場傾斜裂紋1與孔洞周邊區域產生的拉伸裂紋2貫通破裂，巖樣破裂時在孔洞邊緣產生拉伸裂紋1#，方向近似與軸向加載方向平行。這表明含孔洞巖體周邊裂隙的存在不一定改變原有的主貫通破裂帶，例如當含孔洞巖樣周邊存在距原主貫通破裂帶較遠、傾角較大的裂隙時，巖樣依然沿孔洞形成主貫通破裂帶。

圖3 不同裂隙距孔洞距離的砂巖破裂模式Fig.3 Fracture modes of sandstone with different fissure distances from hole defect

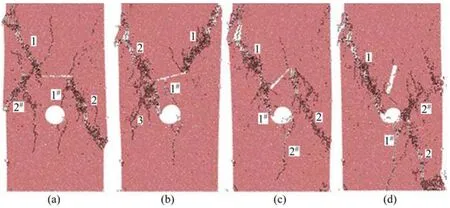
圖4 不同裂隙傾角的砂巖破裂模式Fig.4 Fracture modes of sandstone with different fissure angles

圖5所示為不同裂隙長度2a砂巖試樣的破裂模式。由圖5可知：在相同裂隙傾角下，當2a=10 mm時，孔洞上下邊緣萌生初始裂紋1，2和3，多條裂紋的擴展與貫通導致了巖樣失穩破壞，裂隙的存在基本未影響巖樣破裂模式，巖樣以孔洞為主貫通破裂帶；當2a為15 mm和20 mm時，巖樣的裂紋擴展特征發生改變，由裂隙尖端萌生出的翼裂紋與次生裂紋擴展貫通破裂，未與孔洞之間出現貫通。這表明當含孔洞巖樣周邊存在距原主貫通破裂帶較遠、長度較小的裂隙時，巖樣依然沿孔洞形成主貫通破裂帶。

圖5 不同裂隙長度的砂巖破裂模式Fig.5 Fracture modes of sandstone with different fissure lengths

2.2 砂巖試樣力學特征

圖6所示為不同裂隙形態的含孔洞紅砂巖試樣應力–應變曲線，具體力學參數見表4。由圖6(a)可知：含孔洞砂巖試樣周邊裂隙的存在降低了巖樣的力學參數；在相同裂隙長度下，裂隙距上邊緣距離h=20 mm(105.09 MPa)，h=30 mm(105.85 MPa)和h=40 mm(110.98 MPa)的巖樣與無裂隙巖樣峰值應力112.20 MPa相比，分別降低5.8%，5.7%和1.1%；裂隙與孔洞的距離對含孔洞巖樣峰值應力和峰值應變影響不大，峰值應力隨h的增大而增大的變化規律，h=40 mm的巖樣峰值應力比h=20 mm的巖樣峰值應力提高5.6%，這說明含孔洞巖樣裂隙距孔洞距離越遠，承載能力越強。

由圖6(b)可知：巖樣的峰值應力隨裂隙傾角α幾乎呈線性上升趨勢，α=75°(112.64 MPa)巖樣的峰值應力比α=0°(102.44 MPa)巖樣的峰值應力提高9.7 %。

由圖6(c)可知：裂隙長度2a對含孔洞巖樣的力學參數影響顯著，在相同裂隙傾角下，隨著2a從10 mm增大到20 mm，巖樣的峰值應力由112.80 MPa減小到90.66 MPa，降低約20.0%；峰值應變由1.67 mm減小到1.52 mm，降低9.0%。這說明隨著裂隙長度的增大，巖樣的峰值應力和峰值應變均呈逐漸減小的趨勢。

3 巖體聲發射及損傷演化特征分析

3.1 聲發射特征分析

圖6 不同裂隙形態巖樣應力-應變曲線Fig.6 Stress–strain curves of rock samples with different fissure morphologies

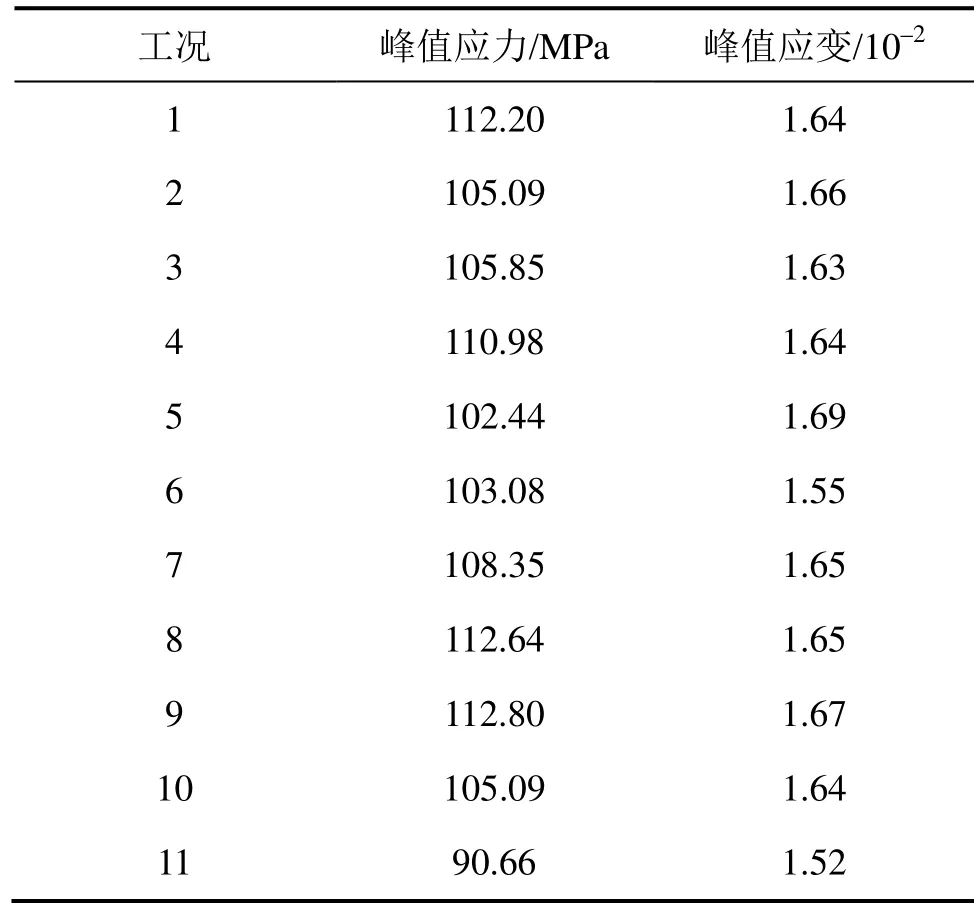
表4 含孔洞砂巖力學參數匯總表Table 4 Mechanical parameters of sandstone containing hole defect

圖7 含孔洞砂巖應力–應變–聲發射特征變關系曲線Fig.7 Stress–strain–AE relationship of sandstone containing hole defect

圖7所示為部分裂隙形態下含孔洞紅砂巖試樣應力–應變–聲發射(AE)特征關系曲線。從圖7可知聲發射演化過程大致分為3個階段：第1階段為聲發射初始階段，該階段對應于應力–應變曲線的彈性階段，聲發射活動次數稀少，甚至為零，這種現象不同于真實巖體，真實巖體在初始階段聲發射活動緩慢增加，這因為PFC平行黏結模型沒有初始損傷，真實巖體內部或多或少具有一定的初始損傷；第2階段為聲發射遞增階段，該階段對應于巖石的塑性階段，聲發射信號急劇增加直到峰值；第3階段為聲發射遞減階段，該階段對應于巖石的損傷階段，聲發射信號不斷降低，直至平穩或為零。缺陷巖樣可能會出現2～3次聲發射振鈴計數高峰，應力在峰后降低到一定程度有反彈現象，分析原因主要在于該巖樣的破裂模式，裂隙尖端萌發的裂紋與孔洞貫通破裂，使巖樣達到峰值強度，但巖樣未完全貫通，繼續加載巖樣產生新的貫通破裂帶時出現新的高峰應力，隨后應力下降。裂隙形態對含孔洞砂巖聲發射特征的影響主要體現在聲發射信號強度與對應的應變上。

3.2 損傷演化特征分析

大量研究表明，聲發射振鈴計數與材料位錯、斷裂和裂紋擴展所釋放的應變能成比例，能很好地反映材料性能的變化[19]。KACHANOV[20]定義了損傷變量D，假設無損的截面面積A完全失去承載力時累計聲發射振鈴計數為N，斷面損傷面積為Am時累計聲發射振鈴計數為Nm，巖石內部的損傷變量D為

由于砂巖試樣在模擬壓縮過程中很難達到完全破壞，引入了損傷修正系數Du這一參數，得修正公式[9]為

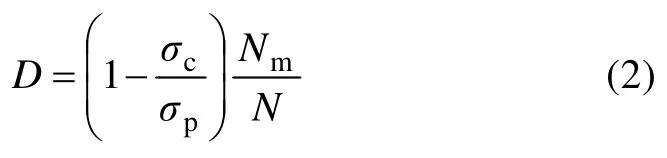
式中：σc為殘余強度；σp為峰值強度。

基于聲發射特性和應變等效原理[21]，建立了單軸壓縮條件下砂巖試樣的損傷本構模型為[12]

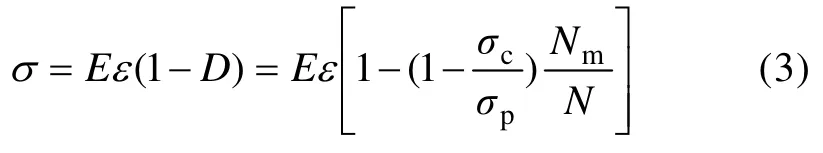
式中：σ為應力；ε為應變；E為彈性模量。

本文以聲發射振鈴計數為特征參數來描述砂巖的損傷演化特性，利用聲發射特征的損傷本構模型方程擬合的應力–應變曲線如圖8所示。從圖8可知：擬合曲線與實際數值曲線相差不大，說明運用基于聲發射參量的砂巖損傷模型來描述砂巖的破裂損傷過程是可行的。

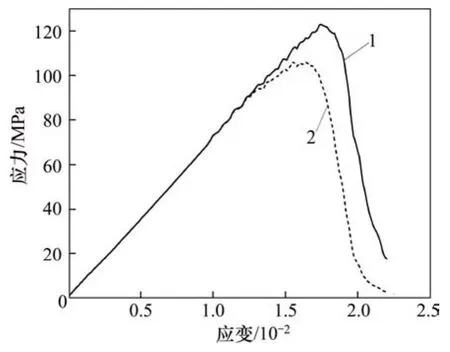
圖8 砂巖理論應力-應變曲線與模擬曲線對比Fig.8 Comparison of theoretical stress–strain curve with simulation of sandstone

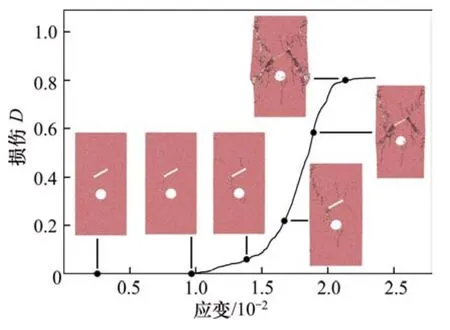
圖9 含孔洞砂巖單軸加載損傷演化過程Fig.9 Damage evolution process of sandstone containing hole under uniaxial compressive load defect

根據式(2)所定義的損傷變量得出紅砂巖試樣在工況2下的砂巖單軸加載破壞過程損傷演化如圖9所示。由圖9可知：在加載初期砂巖內部幾乎不產生損傷，巖樣處于壓密的彈性變形過程；隨著荷載增加，微損傷出現局部集中化趨勢，損傷逐漸在巖樣破壞部位集聚，形成宏觀裂紋；繼續加載巖樣新生裂紋萌發，隨后形成明顯的裂紋擴張方向和演化形態，表明巖樣內的微裂紋迅速擴展、匯合，局部出現宏觀破壞，此時巖樣的承載性能迅速下降，損傷變量急劇上升；之后進入損傷平穩階段，微裂紋的衍生和擴展逐漸趨于穩定，巖樣失去承載能力。

圖 10所示為不同裂隙形態含孔洞巖體紅砂巖試樣的應變與損傷關系曲線，由圖10可知：裂隙幾何形態主要影響含孔洞巖體損傷演化過程中的損傷平穩階段及對應的應變。相同裂隙長度的含孔洞砂巖裂隙距孔洞距離h越遠，在同應變下巖樣損傷越小；對于不同的裂隙傾角α，Du也不同，例如裂隙傾角為 15°時Du約為0.90，而裂隙傾角為45°時Du約為0.77；相同裂隙傾角的含孔洞砂巖裂隙長度 2a越大，在同應變下，巖樣損傷越小。表5所示為含孔洞砂巖的損傷修正系數Du。從表5可以看出：不同裂隙幾何形態的含孔洞巖樣存在不同的Du，Du取值為0.77～0.90。

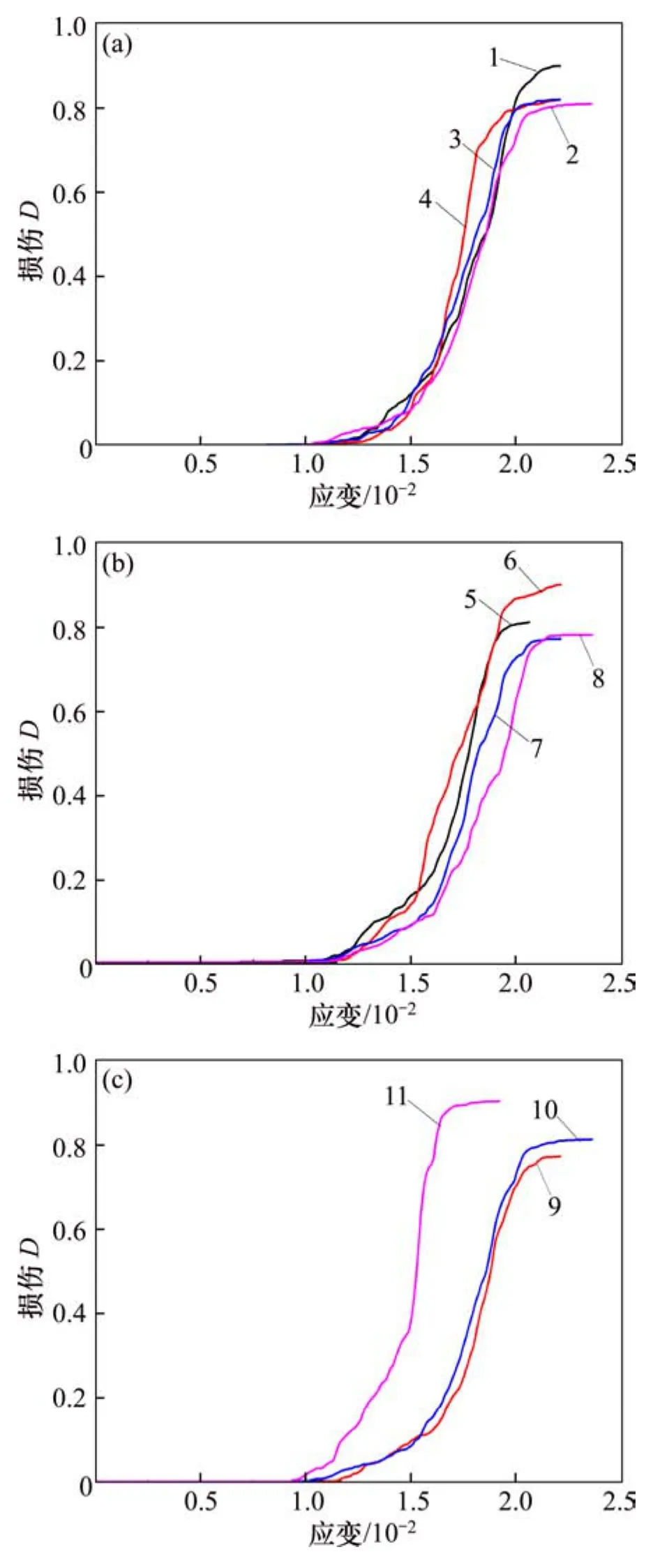
圖 10 含孔洞砂巖應變-損傷變量曲線Fig.10 Strain–damage curves of sandstone containing hole defect

表5 含孔洞砂巖損傷修正系數Table 5 Damage correction coefficients of sandstone containing hole defect

4 結論

1)裂隙的存在會改變原有含孔洞試樣沿孔洞貫通破壞的破壞模式，大多數試樣會形成貫通裂隙的主破裂帶。孔洞上下邊緣萌生初始裂紋，多條裂紋的擴展與貫通導致巖樣失穩破壞，這表明當含孔洞巖樣周邊存在距原主貫通破裂帶較遠，且傾角較大或長度較小的裂隙時，巖樣依然沿孔洞形成主貫通破裂帶。

2)含孔洞砂巖試樣周邊裂隙的存在降低了巖樣的力學參數。巖樣的峰值應力隨裂隙距孔洞距離h的增大而增大的變化規律，隨裂隙傾角α幾乎呈線性上升趨勢；在相同裂隙傾角下，隨著裂隙長度2a的增大，巖樣的峰值應力和峰值應變均逐漸減小，例如長度為20 mm巖樣的峰值應力比長度為10 mm巖樣的峰值應力降低20%左右。

3)聲發射信息反映了砂巖內部的損傷破壞情況，與其內部原生缺陷的壓密，新生裂紋的萌發、擴展及貫通等演化過程密切相關。含孔洞巖體的聲發射演化過程分為聲發射初始階段、聲發射遞增階段和聲發射遞減階段3個階段。

4)損傷本構模型引入損傷修正系數Du后的擬合曲線與實際數值曲線相差不大，說明修正后的損傷本構方程能更好地模擬砂巖損傷演化過程。裂隙形態主要影響含孔洞巖體損傷演化過程中的損傷平穩階段及對應的應變，含孔洞砂巖周邊存在距孔洞距離越遠，長度越大的裂隙，在同應變下巖樣損傷越小；不同裂隙形態的含孔洞巖樣存在不同的損傷修正系數Du，Du取值為0.77～0.90。