可變速機組無位置傳感器控制技術研究

田 煒，常鵬飛，周百靈

（國電南瑞科技股份有限公司，江蘇省南京市 211103）

0 引言

可變速抽水蓄能機組采用的矢量控制策略需檢測轉子位置，常規的轉子位置檢測方法是安裝光電編碼器，但安裝在抽蓄機組中的編碼器易損壞[1]，且安裝難度較大，后期維護成本高，還存在同心度的問題，從而導致檢測位置與實際位置不一致。

因此，采用無位置傳感器的控制方法受到重視：基于控制對象數學模型的直接計算方法[2-3]，但其數學模型對參數有依賴性，位置估計精度不高；有基于電機結構的不對稱性的電感變換方法和高頻注入方法[4-5]，但在極對數較多、表面貼式的工程電機應用時，會由于凸極效應較弱而失效；有基于狀態觀測器的位置估計方法[6]，通過重構被觀測對象的狀態空間模型，消除誤差，對參數變化的魯棒性較好。其中，擴展卡爾曼濾波法和模型參考自適應法屬于狀態觀測器法。

本文通過構建可變速抽蓄機組的無位置傳感器狀態空間模型，分別設計了擴展卡爾曼濾波器和改進模型參考自適應，通過比較兩種估計方法的位置和速度觀測效果，通過仿真驗證了兩種方法的有效性。

1 無傳感器控制方法

對于可變速機組而言，其高階、強耦合、非線性的特點是無法直接應用KF法的，這里便需要引入擴展卡爾曼濾波器法來解決這一問題，這里將可變速機組的模型抽象并重新描述成EKF問題見式（1）：

式中t——連續時間。

式（1）的系統噪聲和測量噪聲同樣滿足白噪聲的條件。

區別于KF法的是，EKF法需要將非線性的問題線性化，采取的是在y=0點處泰勒展開的方法，這里將狀態方程和輸出方程的兩個函數進行泰勒展開，得到式（2）：

其中g′（x0）是一個n×n維方陣，常常稱為雅各比方陣，其i，j分量見式（3）～（4）

對應的擴展卡爾曼“黃金公式”見式（5）：

式中x——狀態變量；

P、Q——懲罰矩陣。

和卡爾曼濾波器類似，模型參考自適應需要比較可調模型與參考模型的差值v，通過使二者的差值收斂至0，那么可調模型的狀態估計值?x就等于參考模型的狀態值x，進而得到系統的真實狀態值。

不同的理論模型適用于不同的控制環境以及控制目的要求。事實上，根據選用的模型不同，可以有不同的自適應律，本文這里是基于轉子磁鏈的MRAS控制器的設計方法。

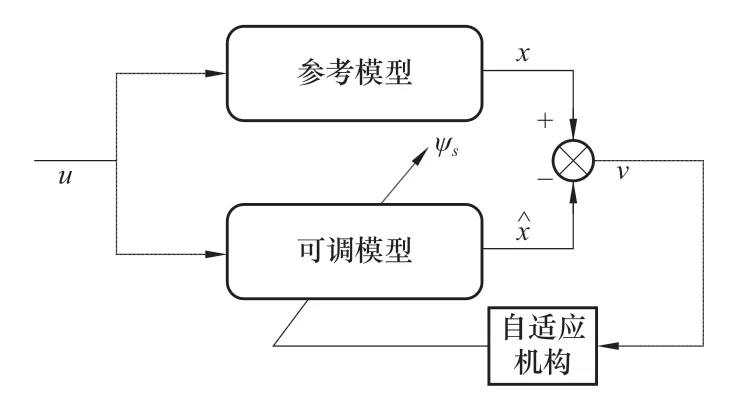
圖1 MRAS結構圖Figure 1 Diagram of MRAS

2 擴展卡爾曼濾波法設計

首先，寫出可變速機組的狀態空間方程，見式（6）：

式中iαs/iβs——定子側電流在α/β上的分量；

ψαr/ψβr——轉子側電流在α/β上的分量；

uαs/uβs——定子側電壓在α/β上的分量；

uαr/uβr——轉子側電壓在α/β上的分量；

ω——轉速，

Tr——轉子轉矩；

Ls——定子電感。

輸出方程見式（7）：

離散化方程（7），按照式（8）：

得到離散化后方程：

則得到式（9）：

將Φ和h對x求導，得式（11）

將上述方程代入黃金公式中去。

3 改進模型參考自適應設計

3.1 確定模型

和EKF法不同的是，MRAS法的模型方程不需要太復雜的推導，但是需要選擇相同的狀態量的不同參數模型，參考模型中不含待估計參數，而可調模型中包括待估計參數，兩者的狀態輸出量差值，作為自適應機構的輸入。根據可變速機組在兩相靜止坐標系中的數學模型，寫出變換后的電壓和磁鏈方程，構造轉子磁鏈的電壓和電流模型：

電壓模型：

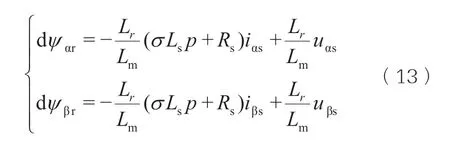
電流模型：

觀察電壓方程不含有待估計量轉子轉速ω，因而電壓模型作為參考模型，而電流模型中含有變量ω，因而電流模型被確定為可調模型。

3.2 確定自適應律

文獻[7]中已經通過對該模型滿足波波夫超穩定要求的理論推導，這里不再贅述，直接給出基于轉子磁鏈的模型參考自適應律如式（15）所示：

顯然，轉速的估計量結果是通過對轉子磁鏈的參考模型輸出值和可調模型的輸出值行叉乘，再進行PI控制得到，這一結論和大多數MRAS法相一致。

3.3 系統框圖

根據上述兩個步驟，這里給出基于轉子磁鏈MRAS法的系統框圖如圖2所示。

圖2 基于轉子磁鏈MRAS法控制系統框圖Figure 2 Control block diagram based on MRAS of rotor flux

同樣的，在離散控制器中，MRAS法存在微分環節σsLs和純積分環節，因此便存在噪聲放大和積分飽和的問題，因此，本文采用一種改進的MRAS法，改寫式（13）為式（16）：

如圖所示，將積分環節用一階慣性環節替代，并且采用對定子磁鏈限幅補償的方式，得到如圖3所示的模型參考自適應的改進電壓模型。

圖3 改進電壓參考模型Figure 3 Model of improved voltage reference

4 仿真驗證

為了比較分析3.2小節中的EKF法和MRAS法的轉子位置估計精度和參數發生變化下的魯棒性，這里對如表1所示電機參數的可變速機組進行Simulink仿真驗證。

表1 電機參數Table 1 Motor parameters

本文分別給出兩種方法在空載和加載情形下的轉速和位置估計效果，并分別給出1000r/min和750r/min兩種轉速條件下的估計效果，研究定子電感偏差下的估計效果。

根據機組的極對數，額定轉速為1500r/min，因此為了分析不同轉速下的位置跟蹤效果，分別給出：1000r/min和750r/min轉速下，兩種方法的估計結果。

圖4 1000r/min下EKF法和MRAS法轉子位置估計值Figure 4 Rotor position of EKF method and MRAS method under 1000r/min

根據圖4，在1000r/min轉速下，圖4（a）為EKF法轉子位置估計值與實際值仿真結果圖，圖4（b）為MRAS法轉子位置估計值與實際值仿真結果圖，對比發現，兩種方法的轉子位置估計值都能夠在第三個周期以后跟蹤實際值。

圖5所示為1000r/min轉速下，兩種方法的位置估計誤差，圖（b）MRAS法的誤差超調量（-1.1rad）顯著大于圖（a）EKF法的誤差超調量（0.43rad）。兩者的穩態估計誤差均在0.02以內，但MRAS法估計誤差在0.15～0.18s以后進入穩態，而EKF法則在0.25s后進入穩態。

從圖6中可以看出，兩種方法的轉速給定為1000r/min，觀察二者發現，MRAS法相較于EKF法對轉速的估計，前者的響應速度更快，但超調更大，而且0.5s之前的估計值穩態誤差也更大，但兩者對于速度的跟蹤都能保持良好的估計效果。

圖7所示為轉速估計值與實際值的誤差曲線，可以定量的看出，EKF法的轉速超調不超過100r/min，而MRAS法的轉速超調最大為-600r/min，換言之，機組在起動的過程中有一個短暫的反轉過程，然后才能進入正常起動狀態；在進入穩態以后，EKF法的轉速估計誤差在-10～10r/min范圍內，而MRAS法在0.5s之前的轉速誤差波動范圍達到-200～200r/min，0.5s以后其誤差絕對值也在20r/min附近。

圖4～圖8的估計結果均是在可變速機組空載的情況下仿真得到的，為了進一步比較兩者在加載以后的動態跟蹤效果，接下來進行0.5s加載的仿真對比，并進一步比較750r/min下加載的穩態和動態性能。

圖5 1000r/min下EKF法和MRAS法轉子位置估計誤差Figure 5 Rotor position error of EKF method and MRAS method under 1000r/min

圖6 1000r/min下EKF法和MRAS法轉速估計值Figure 6 Rotor speed of EKF method and MRAS method under 1000r/min

圖7 1000r/min下EKF法和MRAS法轉速估計誤差Figure 7 Rotor speed error of EKF method and MRAS method under 1000r/min

圖8 1000r/min下EKF法0.5s加載估計誤差Figure 8 Loading estimation error of EKF method under 1000r/min when 0.5s

首先在1000r/min仿真運行至0.5s，進行加載，如圖9所示，為EKF法加載后的轉速估計誤差和位置估計誤差，可以發現，轉速估計誤差在加載瞬間發生超調突變（30r/min以內），但在經過0.02s后又能恢復穩態；觀察位置估計誤差發現，其誤差值大小同樣會在加載瞬間突變，但經過0.05s后恢復穩態，但穩態誤差值相較于空載情況下增大，但依然在0.05rad以內。

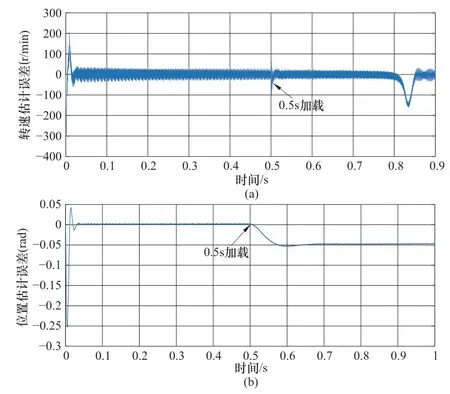
圖9 1000r/min下MRAS法0.5s加載估計誤差Figure 9 Loading estimation error of MRAS method under 1000r/min when 0.5s

如圖9所示為MRAS法在0.5s加載前后的轉速和位置估計誤差曲線，轉速估計誤差在加載瞬間的超調量達到了-150r/min，在0.01s后迅速恢復，但此時的轉速已經不穩定，在0.84s左右出現誤差抖動增大的情況；同樣的，位置估計誤差在加載以后同樣出現了偏差增大的問題。

進一步地，如圖10所示，在750r/min仿真運行下，進行0.5s加載驗證，對于EKF法轉速估計誤差結果，其起動轉速誤差超調縮小至-400r/min以內，但0.5s加載后的轉速估計誤差超調增加，恢復時間也增長至0.04s；同樣的，EKF法的位置估計誤差在起動階段的超調量也下降至0.5rad，但加載瞬間的誤差超調量也明顯增加，并且恢復后的穩態誤差也大于加載前，這與1000r/min下的結論是一致的。

在圖11中，對于MRAS法轉速估計誤差結果，在750r/min仿真條件下，最顯著的特點是其轉速估計誤差絕對值從原來的200r/min降到了40r/min，起動轉速超調量也顯著下降，說明MRAS法對于低穩態轉速的估計效果更為良好。但帶來的問題也是不可忽視的，在0.5s加載瞬間，其轉速估計誤差超調至-430r/min，遠遠大于1000r/min下的-150r/min的加載超調量，并且加載以后的轉速誤差在0.69s附近發生抖動，說明加載后的轉速估計效果下降。而對于MRAS法位置估計誤差結果，750r/min運行下的位置誤差調節時間也顯著增加，而且加載后的穩態誤差也顯著增加。

圖10 750r/min下EKF法0.5s加載估計誤差Figure 10 Loading estimation error of EKF method under 750r/min when 0.5s

圖11 750r/min下MRAS法0.5s加載估計誤差Figure 11 Loading estimation error of MRAS method under 750r/min when 0.5s

綜上所述，EKF法和MRAS法仿真比較發現，無論是在空載情況下還是加載以后，對于轉速估計精度而言，EKF法是顯著優于MRAS法的，并且EKF法對于突變負載的魯棒性更好；對比兩種方法在1000r/min和750r/min下的仿真結果，雖然MRAS法在750r/min下的轉速估計誤差結果同樣理想，但其加載以后的超調量和穩態誤差偏大，其位置估計誤差也存在同樣的問題。

5 結束語

通過對可變速抽蓄機組的建模，研究了擴展卡爾曼濾波和改進MRAS兩種無傳感器轉子位置辨識方法，并分別對兩種方法進行觀測器設計。其中，針對常規MRAS法存在微分環節和積分偏差問題，針對電壓參考模型進行了改進。通過仿真比較兩種方法在不同轉速以及加載前后的轉子位置和轉速觀測效果，得出擴展卡爾曼方法效果更佳的結論。