變壓器繞組匝間短路電動力的研究

關羨濱，滕 躍，張洪坤，鮑 峰，張秀紅

[1.松花江水力發電有限公司吉林白山發電廠，吉林省吉林市 132013；2.華潤電力（錦州）有限公司，遼寧省錦州市 121006]

0 引言

變壓器繞組匝間短路故障具有檢測困難、電動力劇烈和危害大等特點[1]。變壓器故障的統計資料顯示，由于匝間短路故障辨識難度大導致變壓器設備損壞的比重較高[2]。差動保護作為變壓器的主保護，在處理該故障時存在失效或拒動的問題，從而導致長期負載運行的繞組出現嚴重變形、絕緣損壞等惡劣后果[3]。

短路電抗法、頻率響應法和低壓脈沖法等作為變壓器繞組形變的傳統檢測方法，在檢測過程中具有運輸困難、試驗費用昂貴、接線復雜以及耗時長等缺點，已經不適用快速發展的電力系統[4]。機械振動法作為在線監測法中的一種，具有操作簡單、對設備影響小以及費用低等優點，能夠安全可靠地監測設備的運行狀態，具有較好的應用前景[4]。變壓器繞組短路故障時電流激增以及受力劇烈，是變壓器繞組振動的主要原因，因此對變壓器繞組電動力的研究有助于分析變壓器繞組的振動與形變特性。近年很多學者基于場路耦合原理研究變壓器內部故障時磁場問題[5]。文獻[6]利用有限元法研究變壓器的直流偏磁效應，雖然考慮了變壓器故障時的電磁特性，但是二維模型的計算誤差較大。國內外已有文獻研究變壓器繞組外部短路時的電動力，通過對比二維和三維仿真模型下的短路電動力，說明三維電磁模型更具有適用性[7]。文獻[8]利用有限元法仿真分析短路繞組的軸向和徑向電動力，但是沒能考慮安匝不平衡對繞組電動力的影響。已有研究表明，變壓器繞組匝間短路對設備運行乃至系統穩定產生了極大危害，雖然這一問題引起了國內外的廣泛關注，但是罕有文獻對變壓器繞組匝間短路電動力進行分析。

本文基于場路耦合原理，提出一種變壓器繞組匝間短路電動力分析方法。通過建立變壓器三維有限元磁場模型，模擬繞組匝間短路故障時諧電磁環境，結合時域微分電路模型分析變壓器故障時繞組電磁力的變化情況，并總結其規律。最后，通過對比數值仿真與物理實驗驗證仿真模型的正確性和有效性。

1 變壓器繞組匝間短路仿真模型

變壓器繞組作為多自由度機械系統，變壓器繞組的電動力使用虛位移法[9]計算：

式中Fr——作用在r方向的電磁力；

Wm——繞組漏磁場的磁場儲能；

i和LD——基于場路耦合計算得到的繞組電流和電感。

基于變壓器時域場路耦合電磁仿真模型進行繞組匝間短路電動力分析，由式（1）可知動態電感和時域電流為繞組電動力關鍵的電磁耦合參數，其中等效電路模型計算時域電流，三維等效磁場模型計算動態電感。

1.1 磁場模型

基于磁場模型分析變壓器勵磁非線性問題，采用棱邊有限元法以及矢量磁位A，建立變壓器磁場模型：

式中μ——磁導率，

J——電流密度矢量。

依據棱邊有限元法求解模型磁場區域的整體插值函數為：

式中 {Mn，n=1，2，…，nn}——基函數序列，n——序列編號，nl——總棱邊數。

依據格林定理對上式求解，可得相應磁場區域的伽遼金加權余量方程：

式中 {Mm}——權函數序列，

m——序列編號。

磁場模型中若已知電流i，將加權余量方程離散形成代數方程組，求解可得A，進而計算磁場能量。

1.2 電路模型

變壓器磁鏈方程為：

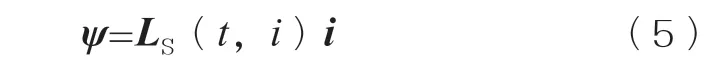
式中ψ——模型的磁鏈向量；

Ls（t，i）——靜態電感矩陣；

i——電路模型的繞組電流；

利用變壓器內部基本電磁關系，可知時域電路微分方程為：

式中u——電壓激勵；

LD——動態電感矩陣。

若tk時刻的線圈電流為ik，利用四階龍格庫塔法對電路模型中建立的方程求解，可知tk+1時刻的電流ik+1為：

式中h——步長，

s1～s4——步長內的分段計算斜率。

基于能量擾動的思想，若線圈電流增加Δi時，將電源總能量與動態電感和電流關聯：

同時，相同電流變化量的條件下，變壓器對應內部系統的磁場能量增量為：

基于變壓器能量轉換過程中的能量守恒原理，聯立式（7）和式（8）可計算動態電感LD。

2 仿真分析

基于場路耦合計算變壓器繞組匝間短路電動力。單相三柱式實驗變壓器參數見表1。

表1 單相變壓器額定參數Table 1 Rated parameters of single-phase transformer

磁場模型求解時在外表面施加磁場平行的邊界條件，電路模型中施加正弦電壓作為激勵，依據場路耦合模型分析變壓器高壓側繞組匝間短路工況下短路繞組電磁力的變化規律。

利用ANSYS/Maxwell建立變壓器三維模型，仿真模型如圖1所示。其中，R1和R2分別表示原、副邊電阻，ZL為負載，N11、N12和N13為高壓繞組，其中N12為短路繞組，N2為低壓繞組。

（1）繞組首端匝間短路。

變壓器空載運行，高壓繞組首端分別設置6%和10%的匝間短路故障，短路線餅分別為1～4號線餅和1～7號線餅。

變壓器繞組首端匝間短路時各線餅受力分布見圖2。

圖1 變壓器匝間短路仿真模型（a）高壓繞組結構；（b）仿真電路圖Figure 1 Simulation model of inter-turn short circuit

圖2 首端繞組電動力分布（a）6%匝間短路；（b）10%匝間短路Figure 2 Force distribution in top winding

由圖2可知，由于不同位置線餅的漏磁通方向各異，造成線餅承受不同方向的拉伸或壓縮力。短路繞組在徑向受力較小，且隨著短路匝數的增大，使得非短路繞組沿徑向的受力值高于短路繞組。短路繞組以及非短路繞組主要承受軸向電磁力，非短路繞組沿軸向受力小于短路繞組。兩種短路狀態都表明短路繞組中，遠離鐵軛的繞組受力值高于靠近鐵軛的繞組受力值，且兩種繞組沿z軸受力的方向相反。

（2）距離首端1/3處匝間短路。

變壓器空載運行，距離高壓繞組首端1/3處分別設置6%和10%的匝間短路故障，短路線餅分別為21～24號線餅和1～7號線餅。

距離高壓繞組首端1/3處匝間短路時各線餅受力分布見圖3。

6%匝間短路時，距離高壓繞組首端1/3處的繞組沿徑向的受力遠小于相同情況時的首端繞組。隨著短路匝數的增大，非短路繞組沿徑向的受力值高于短路繞組。短路繞組以及非短路繞組主要承受軸向電磁力，非短路繞組沿軸向受力小于短路繞組，且非短路繞組沿軸向的受力具有對稱性。

（3）繞組中部匝間短路。

變壓器空載運行，高壓繞組中部分別設置6%和10%的匝間短路故障，短路線餅為31～34號線餅和30～36號線餅。

圖3 1/3處繞組受力分布圖（a）6%匝間短路；（b）10%匝間短路Figure 3 Force distribution in third winding

變壓器繞組中部匝間短路時各線餅受力分布見圖4。

由圖4的可知，中部繞組短路時，隨著短路匝數的增多，非短路繞組沿y方向承受應力增加幅度高于沿x方向的受力情況，且受力值前者高于后者。短路繞組以及非短路繞組主要承受軸向的電磁力，短路繞組軸向電磁力高于非短路繞組，合力的最大值分布在短路匝的兩端。同時，短路匝兩端沿軸向的受力方向相反，且具有對稱性。

3 實驗驗證

繞組振動加速度是電磁力激勵下的強迫振動，將首端短路線餅電磁力作為簡諧激勵源，進行諧響應仿真分析。考慮鐵心振動的影響，分別量測鐵心與繞組的振動情況，利用盲源分離法[10]獲取首端10%匝間短路故障時繞組振動的具體信息，仿真與實驗結果如圖5所示。

由圖5可知，匝間短路時首端繞組振動的仿真與實驗量結果具有一致性，且繞組的振動主頻為100Hz。仿真與實驗的結果表明，該模型能夠有效和正確地仿真繞組匝間短路的受力值。

研究表明，通過建立變壓器匝間短路電磁模型，開展變壓器繞組匝間短路電動力的仿真分析，有助于解決變壓器故障時繞組的受力影響，進而預測繞組在短路沖擊下的變形情況。

圖4 中部繞組受力分布圖（a）6%匝間短路；（b）10%匝間短路Figure 4 Force distribution in middle winding

圖5 變壓器繞組首端振動頻譜圖Figure 5 Vibration spectrum in top winding

4 結束語

利用時域場路耦合模型研究變壓器繞組匝間短路問題，得出以下結論：

（1）繞組在不同位置發生匝間短路時，端部匝間短路所產生的電動力更為惡劣。結果表明場路耦合模型能夠有效模擬變壓器繞組匝間短路時的內部磁場環境，仿真振動諧響應與振動頻譜圖對比驗證了本文方法的正確性。

（2）電動力仿真結果表明，短路繞組主要承受軸向電磁力，端部繞組匝間短路時，線餅受力較為嚴重。首端及距離高壓繞組首端1/3處繞組匝間短路時，短路電動力不具有對稱性，中部匝間短路時，短路電動力具有對稱性。