基于ADAMS的串聯式6自由度平臺仿真分析

鄒喜紅，王瑞東，涂國杰，梅 亞

(重慶理工大學 汽車零部件先進制造技術教育部重點實驗室， 重慶 400054)

串聯式6自由度平臺是區別于并聯式的一種運動機構。相對于并聯式而言，它具有精度高、剛度強、穩定性好、可達空間位置廣闊等優點，在汽車領域和航天、航海領域得到密切關注，很多企業投入大量資金進行研發。因此，為了降低平臺的研發成本，縮短設計和優化周期，對其進行仿真分析是必不可少的一個環節[1-3]。

運動學與動力學仿真軟件有很多，如ADAMS、solidworks、Matlab等。本文以串聯式6自由度平臺為研究對象，在ADAMS中建立仿真模型，充分發揮ADAMS Motion模塊的仿真功能，對模型進行運動學與動力學仿真，包括對作動器位移、速度、加速度運動特性的分析以及驅動力、扭矩動力特性的分析。該方法提高了工作效率，節省了研發時間，并為后續的優化和控制提供了參考，同時為電池包等汽車零部件道路模擬試驗提供了條件。

1 串聯式6自由度平臺結構與原理

串聯式6自由度平臺是一種具有6自由度運動能力的機構。如圖1所示，平臺主要包括：① 動平臺，用于承載負載(被試件)；② 液壓作動器，共6個，用于實現驅動；③ 轉動塊3個，用于實現運動換向；④ 連桿3個，用于連接動平臺與轉動塊；⑤ 鉸鏈，包括6個球鉸、6個虎克鉸，用于固定連接兩個構件；⑥ 靜平臺，即機構的底座。該串聯式6自由度平臺通過6個液壓作動器的伸縮來實現橫移、縱移、升降、橫擺、側傾、偏航6個自由度的運動以及它們的組合運動。

圖1 串聯式6自由度平臺簡圖

2 串聯式6自由度平臺三維建模

2.1 ADAMS三維模型

在ADAMS/View模塊中建立6自由度平臺三維實體模型，建模過程主要分為以下3步：① 在菜單欄下設置工作柵格、坐標系和單位；② 根據平臺各部件的外形尺寸運用幾何建模工具箱進行各部件的實體建模；③ 以靜平臺為基準，依次根據裝配關系完成靜平臺、動平臺、作動器、轉動塊、球鉸等部件的裝配。完成的三維裝配模型如圖2所示。

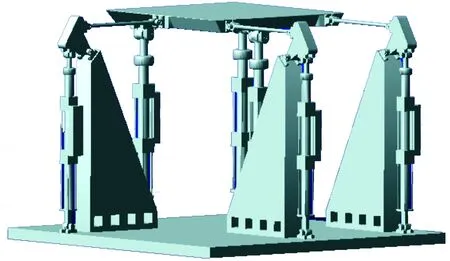
圖2 三維裝配模型

2.2 ADAMS環境下添加約束和驅動

本文采用6個作動器來控制6個方向的運動，根據Kutzbach Grubler公式可知：

式中：F為機構自由度；n為構件總數(包括機架)；m為運動副；fi為第i個運動副的自由度。

從平臺的三維模型中可以看出：垂直方向(z軸方向)有3個作動器，作動器底部與靜平臺用虎克鉸連接，頭部與動平臺為球鉸接觸；橫向(x軸方向)有1個作動器，縱向(y軸方向)有2個作動器，作動器頭部通過轉動塊與連桿連接，底部與靜平臺為鉸鏈接觸；連桿與動平臺為球鉸接觸，與轉動塊為虎克鉸連接。根據機構的等效原理，對橫向和縱向的作動器進行簡化，簡化結果如圖3所示。

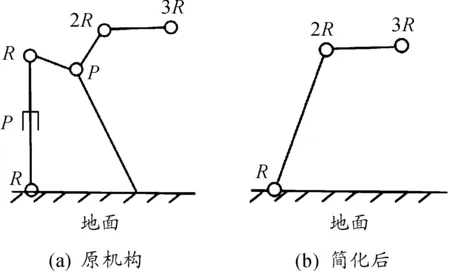
圖3 機構簡化

移動副、轉動副具有1個自由度，虎克鉸副有2個自由度，球鉸副有3個自由度，構件數為14個；運動副共有18個，包括3個轉動副、6個虎克鉸副、6個球鉸副。由于簡化后的模型不存在過約束和冗余結構，所以機構的自由度為

在ADAMS/View環境下，運用運動副工具箱按照平臺要求依次添加所需運動副。ADAMS會根據構件數量、運動副類型以及所加驅動的類型和個數對機構的自由度進行驗證，結果會在信息窗口顯示。從圖4中可看出，經過ADAMS模型檢查以后，機構的自由度為6，所添加的運動副與理論吻合。

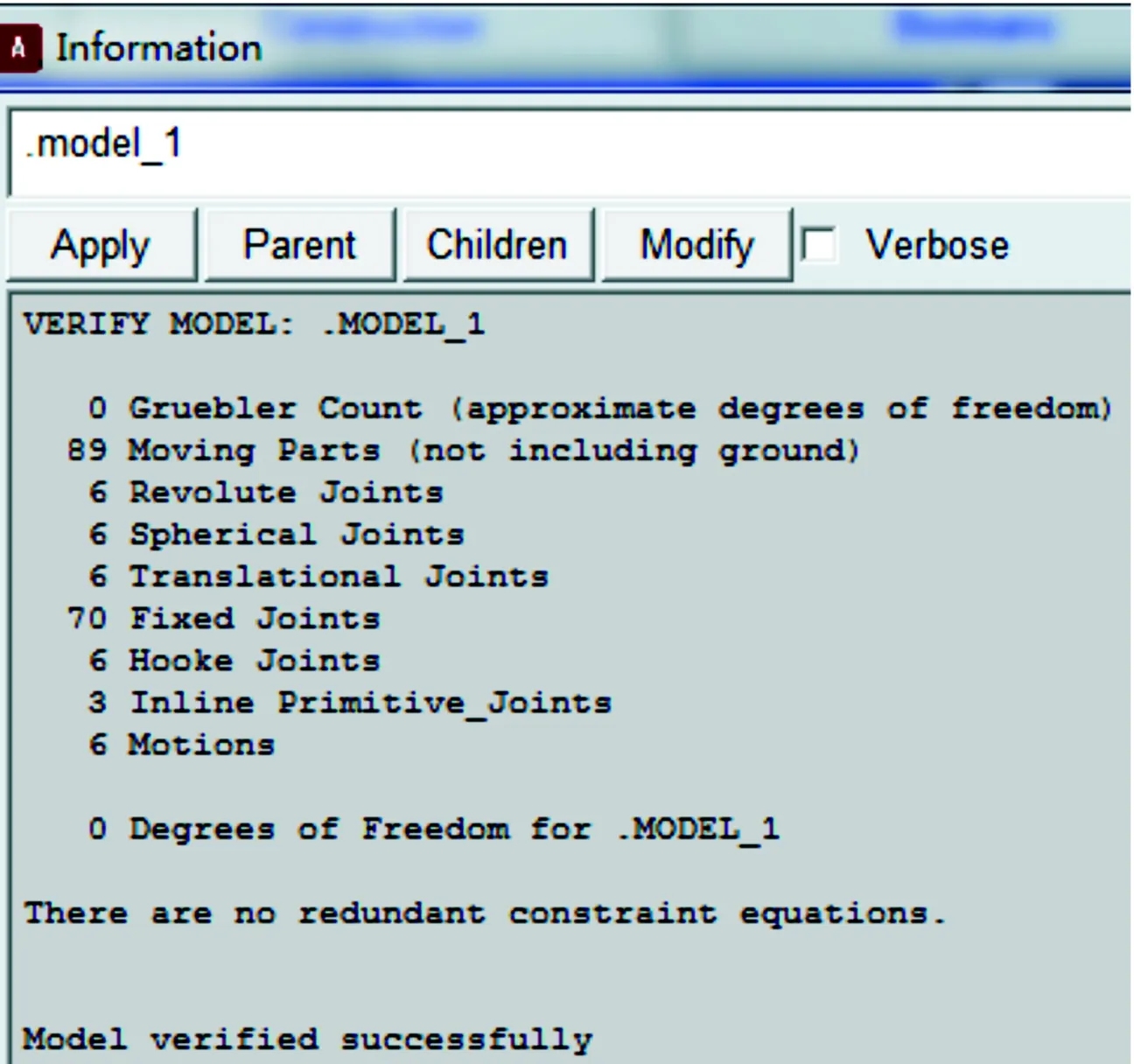
圖4 ADAMS添加約束驅動后的信息窗口

3 串聯式6自由度平臺運動學仿真

為了對串聯式6自由度平臺的運動特性進行分析，給定動平臺一移動和轉動并存的位姿，在ADAMS環境中分析其運動特性及極限位姿。

讓動平臺先沿x、y、z軸3個方向平動，再繞x、y、z軸轉動，分析動平臺與作動器的運動情況。運動位姿參數見圖5。

3.1 動平臺的運動特性

動平臺的運動情況直接決定了被試件的運動軌跡，故其運動特性也決定了被試件的運動特性。

由圖6、7可知：動平臺位移曲線在10～15 s內呈上升趨勢，而在0～10 s和15～30 s內保持不變，這是因為在x、y方向的平動不影響動平臺幅值，只是繞著坐標軸轉動，幅值不發生改變；速度、加速度曲線在15～30 s以及角速度、角加速度在0～15 s內也保持不變，這是因為動平臺的轉動有的只是角速度與角加速度，跟速度與加速度無關；各曲線整體波動比較平穩，無異常點。因此，動平臺的運動特性曲線基本都反映了真實的運動情況。

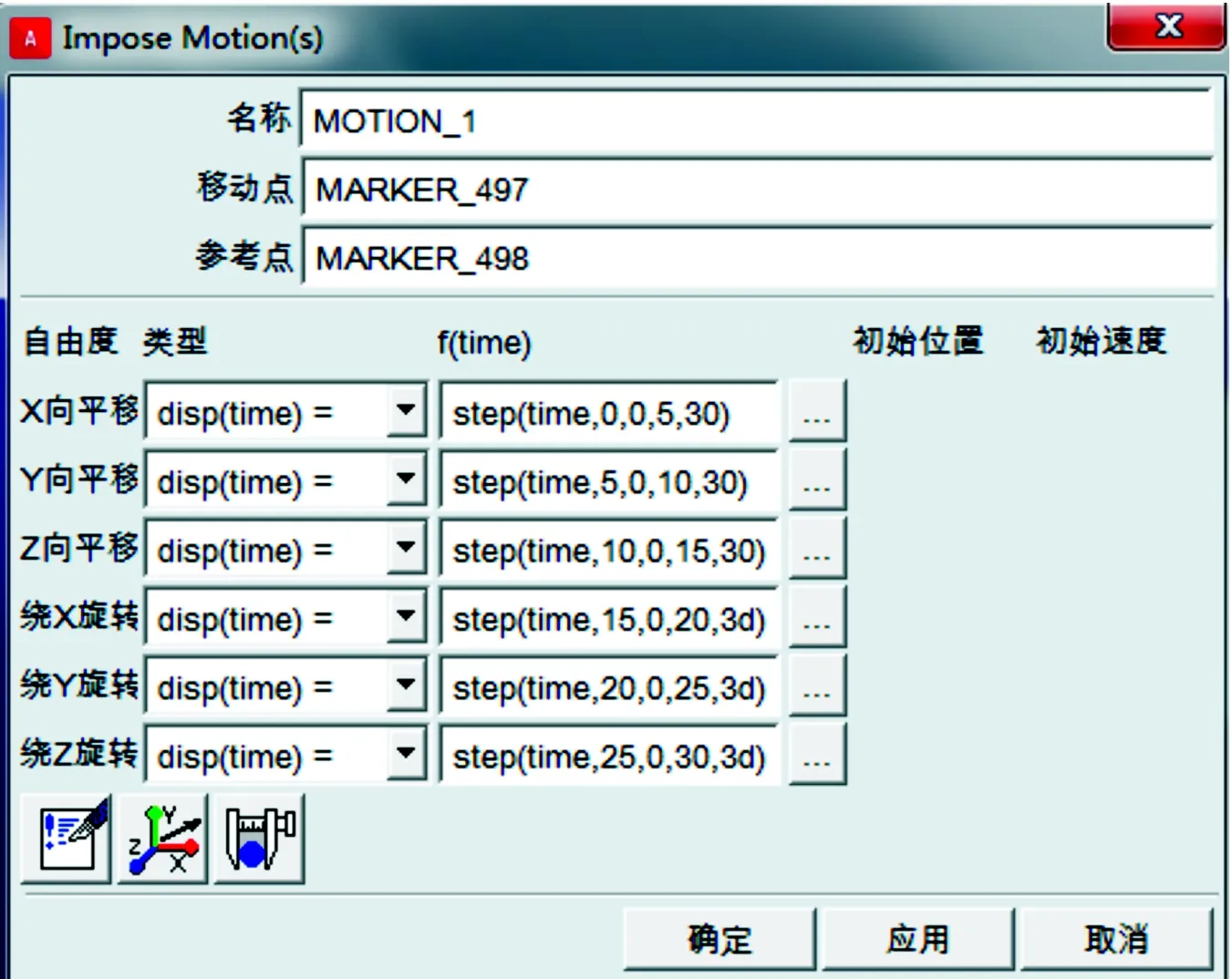
圖5 運動位姿參數

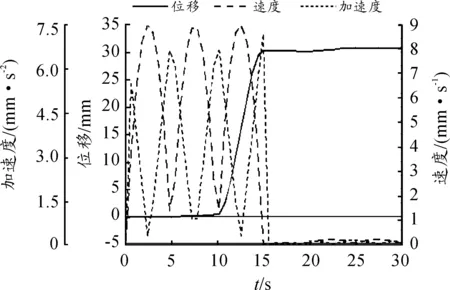
圖6 動平臺位移、速度、加速度曲線

圖7 動平臺角速度、角加速度曲線

3.2 作動器的運動特性

作動器運動特性最直接的表達就是其長度、速度、加速度的變化。由圖8可知：1、2號作動器變化趨勢相同，5、6號作動器變化趨勢互補，與3、4號作動器變化趨勢有明顯差異。出現這種情況的主要原因是作動器分布位置不同以及初始位置的差異使得動平臺在移動后出現各個作動器伸縮量不同造成的，這是不可避免的一種差異。x、y、z三個方向的平動中，z方向的平動作動器伸縮量最大；x、y、z三個方向的轉動中，y方向的轉動作動器伸縮量最大。

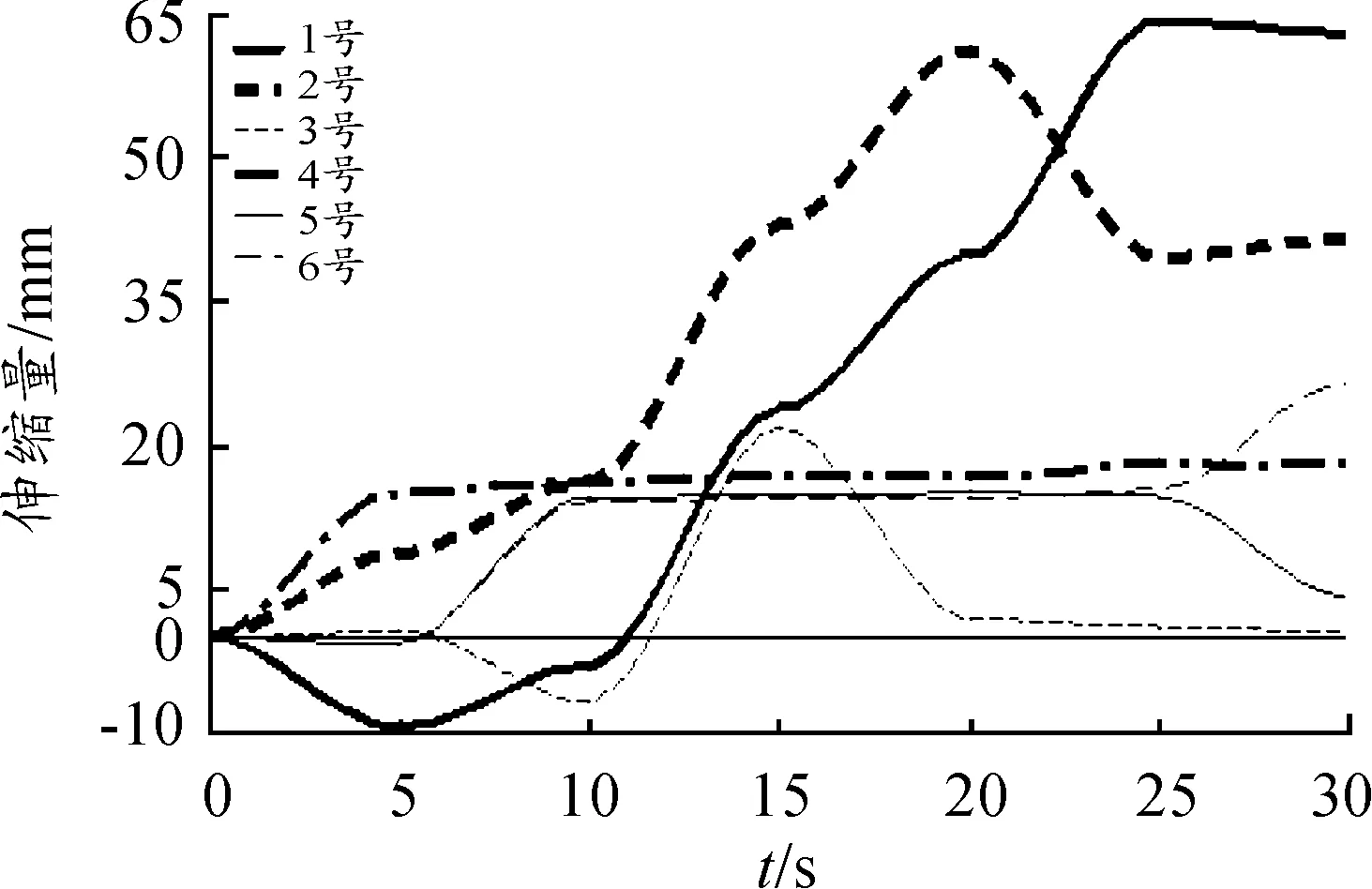
圖8 作動器伸縮量曲線

由圖9、10可知：各作動器速度、加速度運動情況基本一致，曲線整體波動比較平穩。x、y、z三個方向的平動中，z方向的平動作動器速度、加速度最大，x、y、z三個方向的轉動中，y方向的轉動作動器速度、加速度最大。

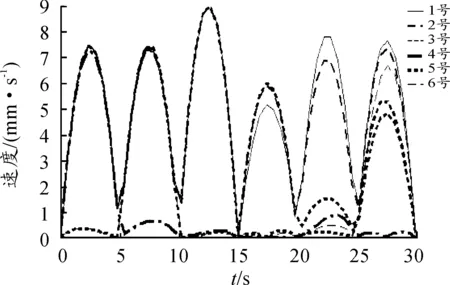
圖9 作動器速度曲線

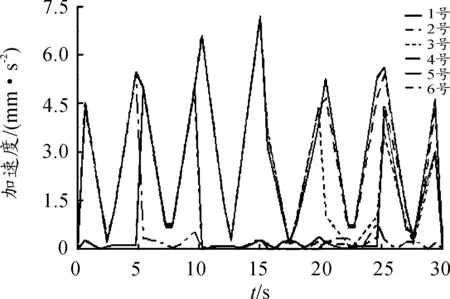
圖10 作動器加速度曲線

3.3 動平臺的極限位姿

在ADAMS View模塊定義測量函數，同時布置傳感器分別對作動器進行位移限制和對球鉸、虎克鉸進行角度限制。給定動平臺一大位姿，當位移和角度超限時仿真停止，仿真停止信息窗口見圖11。

圖11 仿真停止信息窗口

根據仿真結果可得：該平臺x方向所能達的最大位移為70 mm，y方向所能達的最大位移為72 mm,z方向所能達的最大位移為90 mm；x方向所能轉動的最大角度為10°，y方向所能轉動的最大角度為9°，z方向所能轉動的最大角度為12°。

4 串聯式6自由度平臺動力學仿真

4.1 作動器的動力特性

動平臺在運動過程中，其動力特性決定著運動的輸出效果，作動器動力特性主要體現在所受力跟扭矩的變化。

對所設計的串聯式6自由度平臺各構件施加負載，觀察在一定載荷作用下，當動平臺在做位姿變化時，各作動器所受力跟扭矩變化是否平緩，所受力的大小是否符合要求。

由圖12～14可知：各作動器驅動力變化均比較平緩無毛刺；當給定動平臺某一位姿變化時，3號作動器所需驅動力最大；x、y、z三個方向的平動中，z方向的平動所需驅動力最大；x、y、z三個方向的轉動中，y方向的轉動所需驅動力最大。

由圖15可知：3號作動器所受扭矩最大，4～6號作動器次之，1、2號作動器所受扭矩最小。這是因為轉動塊的作用增大了4～6號作動器的扭矩，而3號作動器扭矩最大是因為它承擔了動平臺大部分負載的緣故。x、y、z三個方向的平動中，z方向的平動所需作動器扭矩最大；x、y、z三個方向的轉動中，y方向的轉動所需作動器扭矩最大。各作動器扭矩曲線都比較平緩，基本能夠反映真實情況。

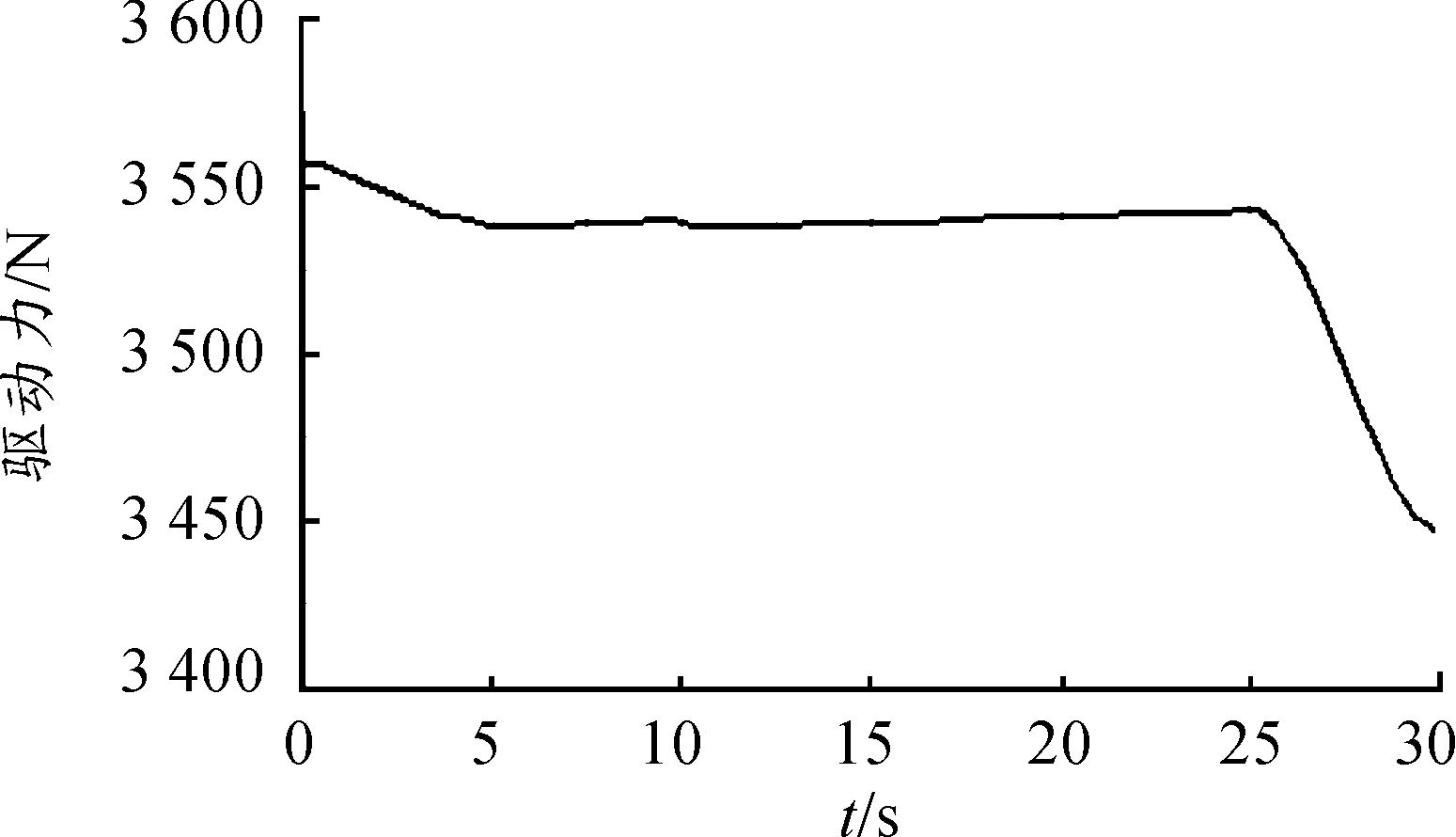
圖12 1,2號作動器驅動力曲線

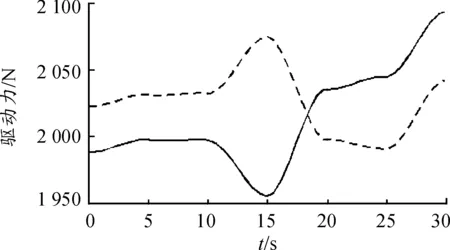
圖13 3號作動器驅動力曲線

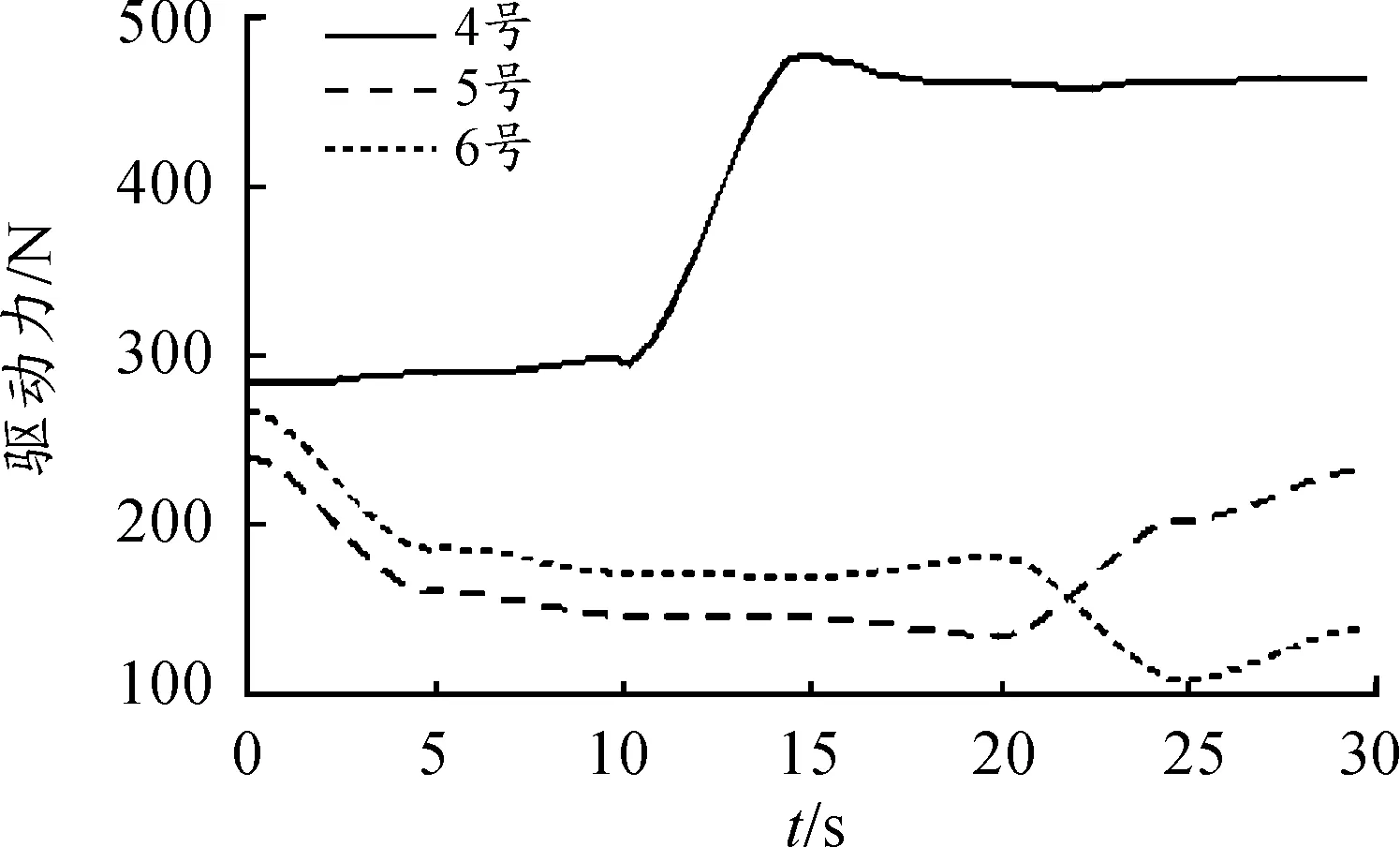
圖14 4～6號作動器驅動力曲線

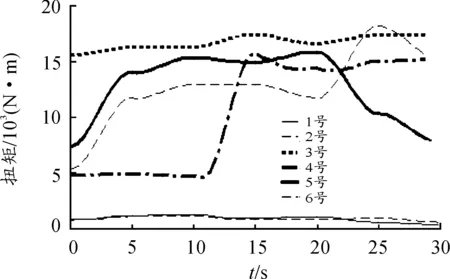
圖15 各作動器扭矩曲線

4.2 動平臺的極限載荷

對動平臺施加載荷，把它簡化為在動平臺質心處施加一垂直向下的力，給定動平臺一位姿，通過改變力的大小來分析該平臺所能承受的最大載荷。因為動平臺在運動過程中，3號作動器所受力最大，所以在這里以3號作動器為研究對象。

由圖16可知，當施加48.9 kN的載荷時,3號作動器的最大驅動力可達24.96 kN,趨近于作動器的最大激振力25 kN，所以此平臺所能承載的最大載荷為48.9 kN。

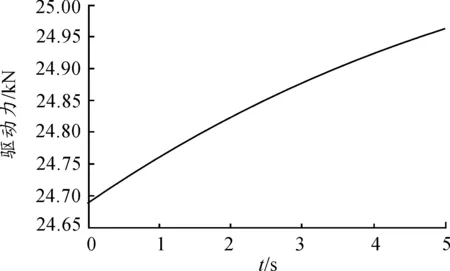
圖16 3號作動器極限驅動力曲線

5 結束語

本文運用ADAMS軟件對串聯式6自由度平臺在6個方向的位姿進行了運動學和動力學仿真，分析了在不同位姿驅動下各作動器運動參數和動力參數的變化規律以及極限位姿和載荷，結果表明：① 在不同位姿驅動下，z方向的平動和y方向的轉動所需作動器伸縮量、速度、加速度、驅動力和扭矩最大，平臺的運動特性和動力特性曲線都比較平緩無毛刺，基本能反映真實情況；② 該平臺所能達的最大位姿為(70,72,90,10,9,12)，高于電池包在實際路面的最大振動位姿，最大載荷為48.9 kN，也遠高于電池包的重力5 kN。本文仿真結果為后續的優化和控制提供了重要的參考，同時為電池包等汽車零部件道路模擬試驗提供了一種方法。