基于ARIMA和BP神經網絡對人民幣匯率預測的比較分析
——以美元人民幣匯率為例

朱家明，胡玲燕

(安徽財經大學 a.統計與應用數學學院; b.金融學院, 安徽 蚌埠 233000)

2005年，我國進行了匯率改革，宣布采用浮動匯率制度，參考一籃子貨幣進行調節，這使我國匯率受到市場供求關系的影響，波動范圍進一步擴大，人民幣出現較大幅度升值[1]。2015年，我國又開展了新一輪匯率改革，宣布當日人民幣中間價需要參考上個工作日人民幣的收盤匯率和一籃子貨幣匯率的變化[2]，這意味著我國匯率制度不斷完善，且不斷向匯率市場化發展。而匯率的波動對個人投資、企業進出口、國家國際收支等來說都有密切關系，因此對匯率走勢進行預測具有重要意義[3]。

國內外學者對匯率預測也進行了相關研究。在國外，Refenes等利用神經網絡和平滑法進行匯率預測，發現神經網絡預測效果更優[4]。而Svitlana則發現神經網絡更適用于對匯率進行短期預測[5]。國內戴曉楓等發現EGARCH對人民幣匯率的預測效果優于ARIMA模型[6]。劉潭秋利用線性和非線性時間序列研究發現LSTAR-GARCH對人民幣匯率的擬合效果更好[7]。而本文分別利用ARIMA和BP神經網絡模型，根據中國貨幣網2017年12月1日至2018年10月8日(除節假日外)的美元兌人民幣匯率數據，對2018年10月9日至10月29日(除節假日外)的15天匯率進行預測，進而判斷模型預測效果，為企業根據匯率走勢把握進出口匯兌風險，個人減低投資風險等提供借鑒。

1 基于ARIMA模型對人民幣匯率的預測效果分析

1.1 研究方法及思路

自回歸移動平均模型(ARIMA)由美國統計學家Box和Jenkins于20世紀70年代提出[7]。ARIMA被廣泛用于時間序列預測分析，其實質是利用差分運算將非平穩時間序列轉化為平穩時間序列，再建立ARIMA模型并進行預測分析。在模型ARIMA(p,d,q)中，p為自回歸階數，d為數據差分次數，q為移動平均階數。模型的基本結構為：

其中，Θ(B)是移動平滑系數多項式，而φ(B)是自回歸系數多項式， {εt}是零均值白噪聲序列[8]。而本文利用ARIMA模型對2018年10月9日至2018年10月29日(除節假日外)的人民幣匯率數據進行預測，并利用2017年12月1日至2018年10月8日(除節假日外)的人民幣匯率數值作為實驗數據，數據均來源于中國貨幣網。首先采用時序圖和ADF檢驗對數據的平穩性進行判斷，若不平穩則作差分再次檢驗，若差分平穩，則對差分序列進行自相關和偏自相關檢驗，初步判斷ARIMA的自回歸階數和移動平均階數，并結合AIC、SC、HQ準則對ARIMA進行識別和定階，選擇最優 ARIMA模型并利用其殘差序列和相關系數對模型效果進行判斷，最后預測數據，并分析預測效果。

1.2 預測分析過程及結論

1) 平穩性檢驗和處理

時間序列建模要求數據平穩，因此首先對原數據的平穩性進行判斷，本文選擇時序圖和較常用的ADF檢驗進行判斷。利用EVIEWS 10繪制出樣本的時序圖，見圖1。由圖1可以看出：數據波動較大，且呈現先下降再上升的總體趨勢，初步判斷數據不平穩，再對其進行ADF檢驗。在ADF檢驗過程中，依次選擇含截距項和趨勢項、含截距項、原序列3種情況進行逐步的檢驗和剔除，得到的檢驗結果如表1所示。可知在5%的顯著性水平下，人民幣匯率數據存在單位根，數據不平穩，因此對原序列進行一階差分，見表1。可知一階差分序列在5%的顯著性水平下平穩，因此可以用其進行ARIMA建模，且在ARIMA模型中差分次數為1。

圖1 人民幣匯率時序圖

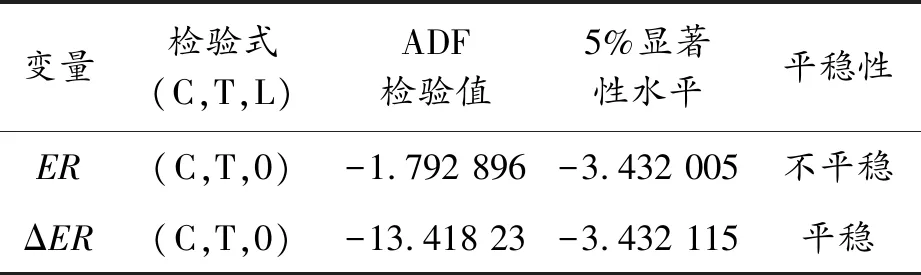
變量檢驗式(C,T,L)ADF檢驗值5%顯著性水平平穩性ER(C,T,0)-1.792 896-3.432 005不平穩ΔER(C,T,0)-13.418 23-3.432 115平穩

2) ARIMA識別和定階

已知一階差分數據為平穩的時間序列，滿足ARIMA模型建立的初步要求，但還需對模型進行識別和定階。目前，廣泛應用的ARIMA識別和定階方法是利用偏自相關系數、自相關系數和AIC、SC、HQ準則進行擬合效果判斷，確定最優ARIMA[9]。因此，本文利用SPSS軟件得到一階差分序列的自相關系數和偏自相關系數及其相關圖，見圖2。可以看出圖形中有較為明顯的拖尾，并初步判斷自相關和偏自相關皆為3階或4階拖尾。為了進一步確定模型的自回歸階數及移動平均階數，分別建立模型ARIMA(3,1,3)、ARIMA(3,1,4)、ARIMA(4,1,3)、ARIMA(4,1,4)，并結合AIC、SC、HQ值綜合確定模型參數(如表2)，發現ARIMA(4,1,3)的AIC、SC、HQ值皆為最小，根據最小化原則，選擇建立ARIMA(4,1,3)模型。

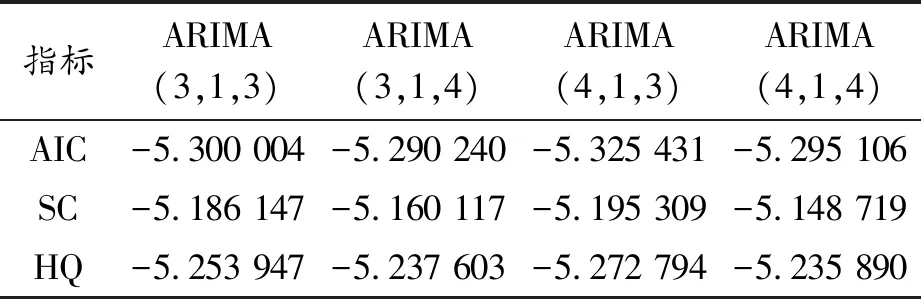
表2 模型精度指標對比

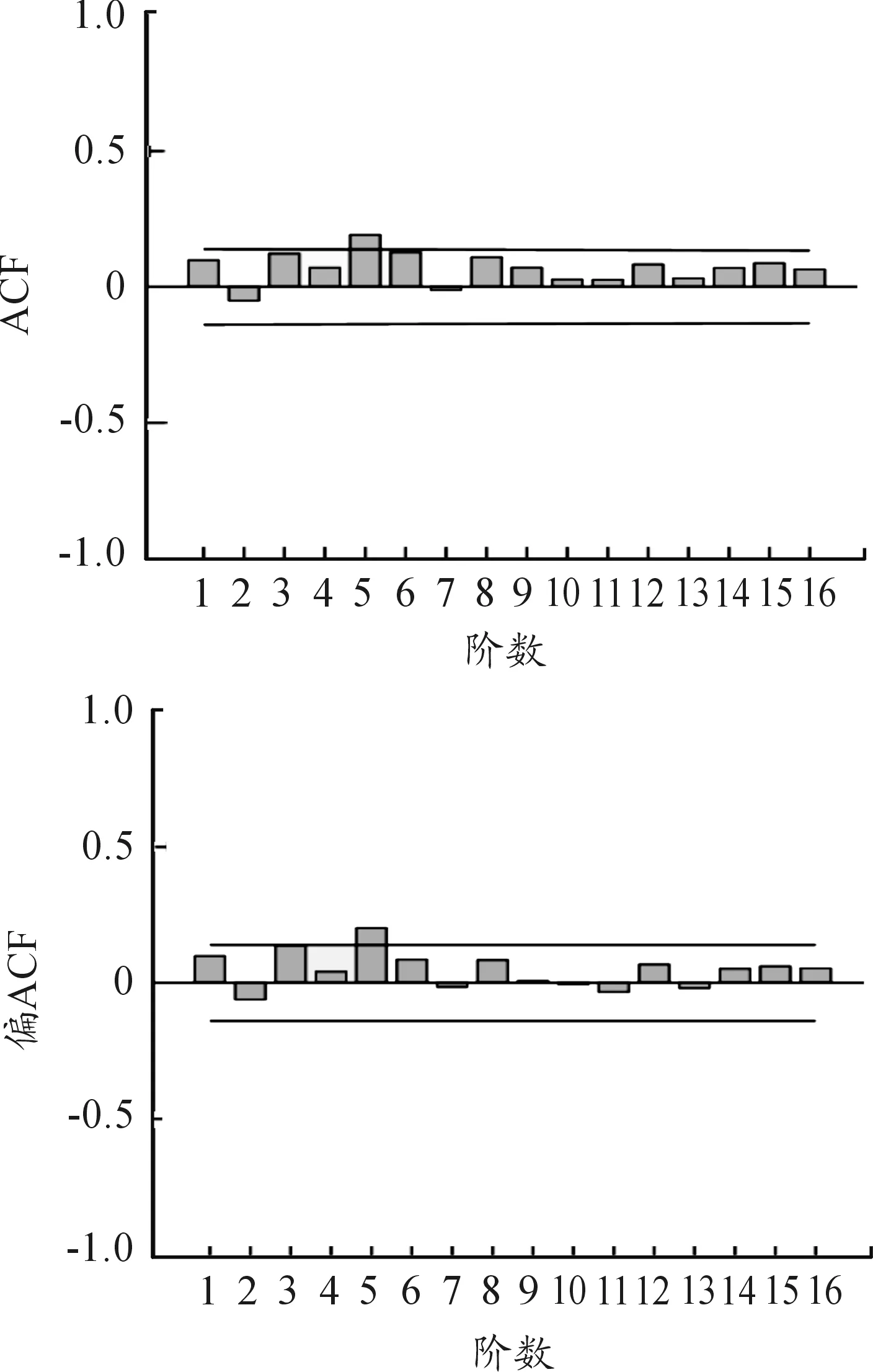
圖2 ACF和PACF圖

3) 模型的檢驗及預測

為了判斷模型的有效性，還需對ARIMA(4,1,3)模型的殘差進行序列和自相關檢驗，見圖3和表3。

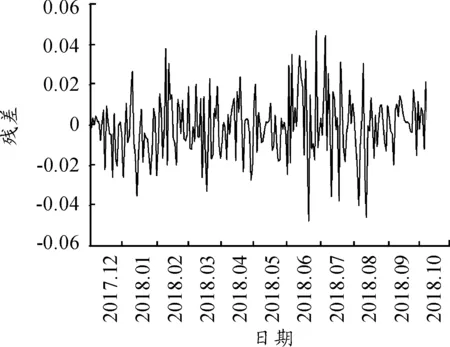
圖3 殘差序列

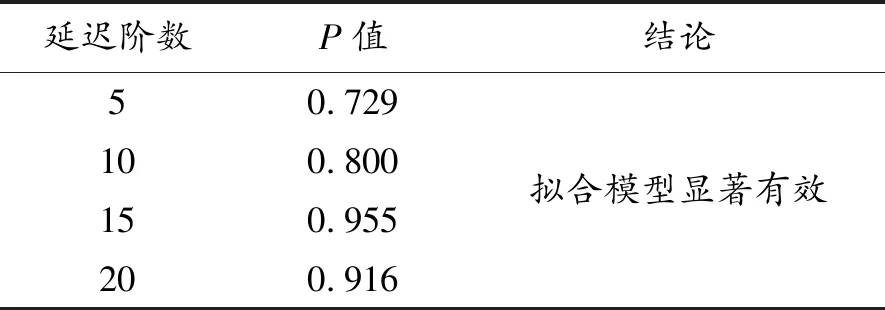
延遲階數P值結論50.729100.800150.955200.916擬合模型顯著有效

由殘差序列圖和自相關檢驗結果可知：模型的殘差序列較均勻地分布在兩側，其自相關系數P值均遠大于0.5，說明殘差序列為白噪聲序列，模型已提取大部分有規律的重要信息。且該模型預測效果較好，因此模型建立有效可行。利用該模型對2018年10月9日至2018年10月29日15個工作日的人民幣匯率進行預測，并與實際匯率數值進行對比，見表4。

表4 人民幣匯率預測結果

由表4可以看出：人民幣匯率真實值與預測值的趨向大體一致，且兩者的相對誤差較小，其中最大相對誤差僅為0.009 777，最小相對誤差為0.000 058，平均相對誤差為0.001 627。說明利用ARIMA模型對人民幣匯率進行預測具有一定的可行性，預測整體效果較好，可以有效預測未來匯率的走勢。此外，隨著預測時間的推移，預測值與實際值的偏差有擴大的趨勢，因此該模擬更適合進行短期的匯率預測。

2 基于BP神經網絡模型對人民幣匯率的預測效果分析

2.1 研究方法及研究思路

人工神經網絡是一種通過模仿人類大腦神經傳遞特征所建立的一種復雜系統，僅依靠數據自身的變化，具有自我鑒別行為模式的能力，因此也被運用于多個領域。而其中BP神經網絡是包含一個輸入層、一層隱含層、一層輸出層的多層前向型神經網絡[10]，其結構如圖4所示。其工作原理是整個工作過程都是按照有“導師”的方式進行訓練，并采用信息向前傳遞和誤差反向傳遞的算法，根據每一次迭代結果逐次修正各連接權，提高模型響應的正確率，直到達到預設的預測精度要求或預設的迭代次數[11]。

圖4 BP神經網絡結構

本文將前4日的美元兌人民幣匯率作為輸入變量，第5日作為輸出變量，并將前186組變量矩陣作為訓練樣本，后15個變量矩陣作為測試樣本。根據計算公式和最小均方差原則設定隱含層神經元個數，并確定BP神經網絡模型的整體結構為4-4-1。然后設定網絡的各訓練參數，包括學習算法、訓練函數、性能函數和傳遞函數等[12]。然后利用Matlab軟件對模型進行訓練，并利用最優訓練網絡對2018年10月9日至2018年10月29日人民幣匯率進行預測，并與真實匯率數據進行比較，進而評價模型的預測效果。

2.2 預測分析過程及結論

1) 模型結構確定及參數設置

首先將2017年12月1日至2018年10月8日的人民幣匯率數據進行有效處理，其中將前4天的數據為輸入變量，第5天為輸出變量，形成一個186行乘以5維的變量矩陣，即模型為4個輸入層和1個輸出層。然后根據公式進一步確定神經元個數[13-14]：

其中d=4,k=1,b為1～10之間的常數。因此，初步確定模型的神經元個數為3～13個，然后結合模型的最小均方差，采用試湊法進行逐個判斷，最后確定隱含層的神經元個數為4。綜上設定BP神經網絡結構為4-4-1。然后對模型的參數進行設定，其中傳遞函數為Tansig，訓練函數為Trainlm，權重和閾值的學習算法以及性能函數分別為Learngdm，Mse。此外，模型的目標誤差為1×10-5，最大迭代次數為1 000次。

2) 模型預測

模型設定完成后，利用模型對數據進行訓練和預測，并利用訓練好的BP神經網絡模型對2018年10月9日至2018年10月29日人民幣匯率進行預測，訓練結果如圖5、6所示。

由圖可知，模型的訓練數據、驗證數據以及測試數據的均方誤差在epoch2前迅速減小，并在epoch10時達到最小值0.000 302 67，此時神經網絡訓練的結果最佳。

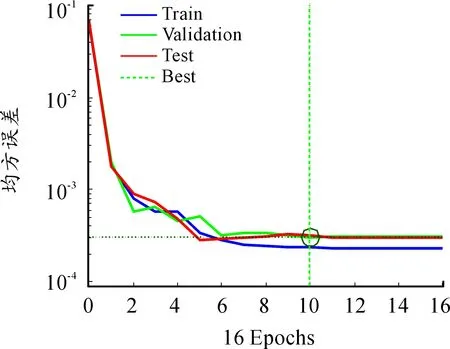
圖5 均方誤差

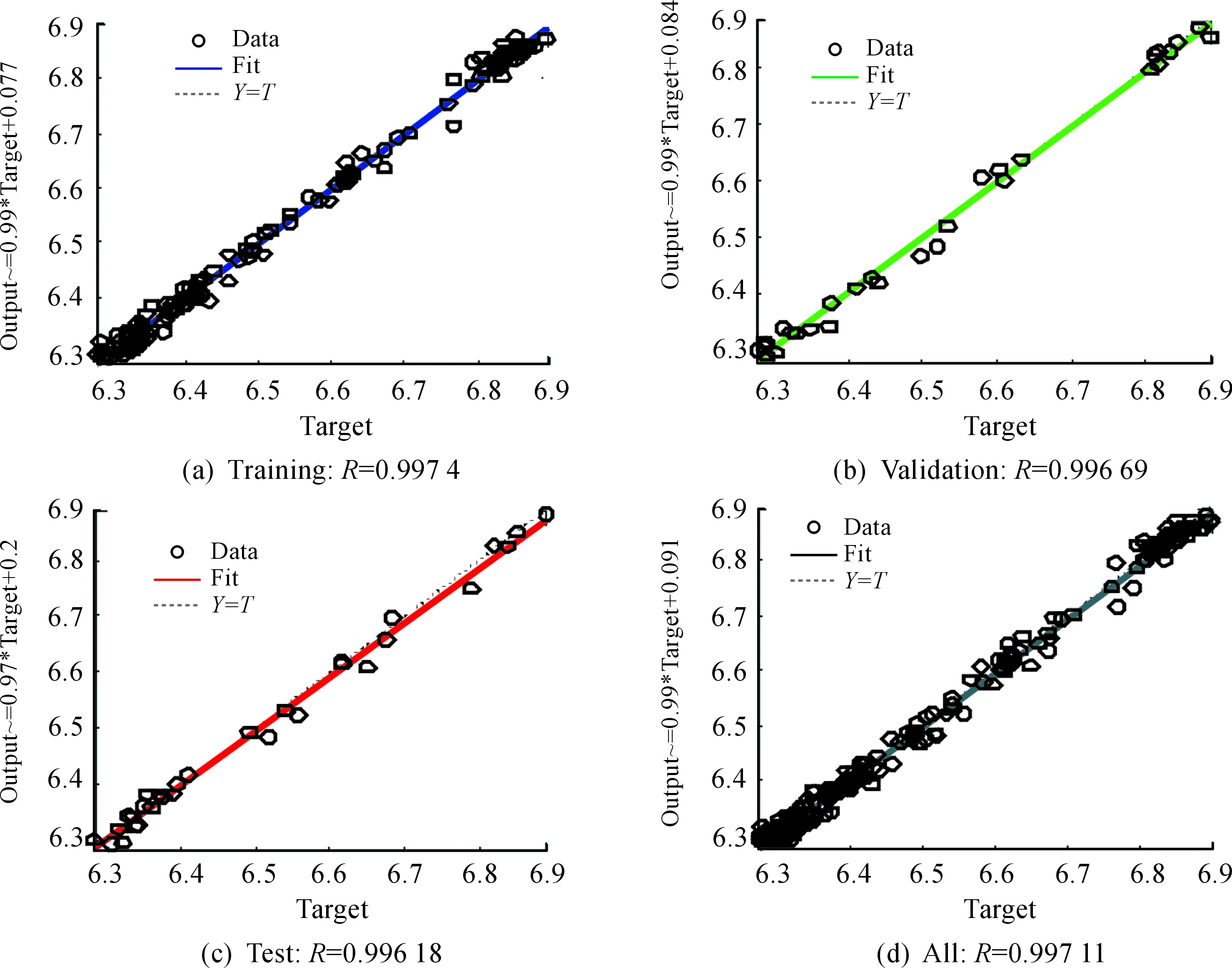
圖6 擬合效果圖

由圖6可知：所訓練的BP神經網絡對數據擬合效果很好，其中訓練數據擬合R值達0.997 4，驗證數據、測試數據及所有數據的擬合R值分別為0.996 69、0.996 18、0.997 11，均大于0.99，模擬擬合效果好，可用于預測2018年10月9日至2018年10月29日人民幣匯率，得到的預測結果如表5所示。

由表5可以看出：人民幣匯率預測結果的整體相對誤差較小，其中最大為0.008 03，最小為0.002 68，平均相對誤差僅為0.004 632，整體來看BP神經網絡預測效果較好，但隨著預測時間的推移，相對誤差有增大的趨勢。因此，BP神經網絡模型對人民幣匯率進行短期預測更有效。而0.004 632>0.001 627，故與ARIMA模型相比，BP神經網絡對人民幣匯率的預測效果較差。

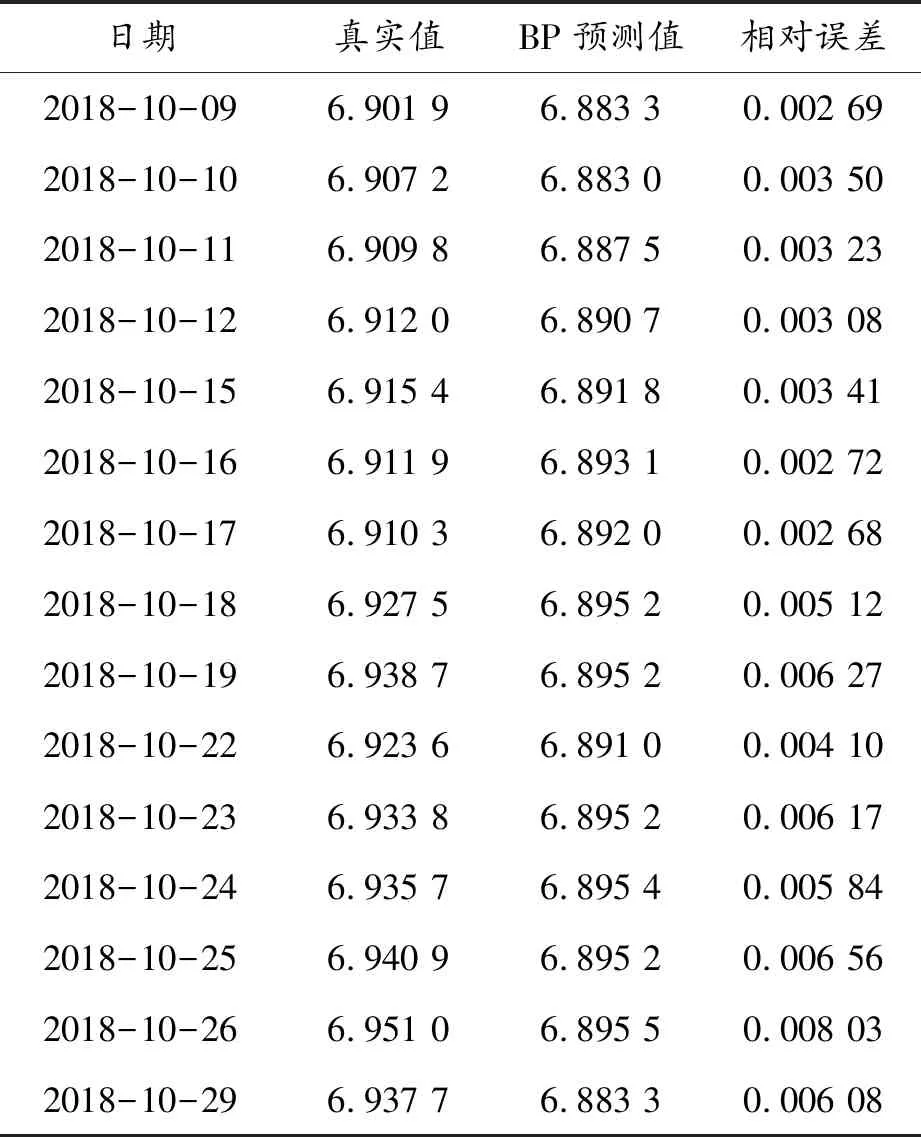
表5 人民幣匯率預測結果

3 結論

本文利用ARIMA和BP神經網絡模型對美元兌人民幣匯率分別進行預測分析發現：

1) 兩模型對人民幣匯率的預測有效，預測精度較高。

2) 相比之下，ARIMA模型的預測效果優于BP神經網絡，相對誤差更小。

3) ARIMA和BP神經網絡對人民幣匯率的預測精度隨著預測時間的推移而下降，兩模型更適用于短期預測。

但本文也存在不足之處，僅用相對誤差判斷模型的預測精度，若能結合未來匯率的變動趨勢進行綜合判斷則更優。此外，僅考慮匯率自身的情況，沒有納入其他影響匯率的重要因素，模型預測結果不穩定。總的來說，本文構建ARIMA和BP神經網絡模型，利用美元兌人民幣匯率為數據，對未來15日匯率進行了預測分析，發現兩模型對人民幣匯率作短期預測是有效、可行的。該模型還可推廣用于股票價格、股指、產品價格預測等方面。