《方程的根與函數的零點》教學設計

徐建新

[摘? ?要] “方程的根”是一個靜態的點，等價轉化為求“函數的零點”的動態過程，體現了“動”“靜”轉化的思想，為利用二分法求方程的近似解奠定基礎 .函數零點存在性定理是判斷函數零點的重要依據，教學的難點在于將“圖像特征”轉化為“代數表示”. 教學設計應注重分析圖像特征，歸納代數表示，提煉定理，為構建靈動的數學課堂做準備.

[關鍵詞]方程的根;函數零點;圖像特征;教學設計

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2019）14-00013-03

一、教學目標

1. 能結合具體函數的圖像，理解方程的根、相應函數圖像與[x]軸的交點以及函數零點的關系，掌握函數零點的概念;

2. 能借助具體函數的圖像，掌握“函數零點存在性定理”;

3. 能利用函數圖像和性質判斷某些函數的零點個數;

4. 能將一個方程求根問題轉化為一個函數零點問題，會判斷函數零點所在的區間;

5. 能體會從特殊到一般、從具體到抽象的認知學習過程，培養函數與方程、數形結合等思想，提升數學抽象、直觀想象、數學運算、數學建模等數學核心素養.

二、 教學重難點

教學重點：函數零點的概念;函數零點與方程的根的聯系;連續函數在某區間上存在零點的判定方法.

教學難點：用函數與方程的思想將方程問題轉化為函數問題;零點存在性定理探究過程中“圖像特征”轉化為“代數表示”.

三、 教學過程

1.創設情境，提出問題

問題1：下列方程有幾個實根？你是如何判斷的？

設計意圖：對于方程（1），學生可用十字相乘法、公式法、判別式法等判斷方程根的個數.但對于方程（2）的“大數據”，若運用方程（1）所涉及的方法會很煩瑣. 因此，可引導學生考慮二次方程與二次函數的關系，思考能否利用二次函數[f（x）=628x2+529x+107]的圖像來判斷根的個數.從學生熟悉的二次方程入手，降低起點. 問題導向從簡到繁，充分調動學生探究未知問題的積極性，開門見山，直接引入本節課的教學內容.

2.回顧舊知，探索新法

問題2：（1）結合圖1，請觀察并說明二次方程[x2-2x-3=0]的根和二次函數[y=x2-2x-3]的圖像與[x]軸的交點的關系;（2）復習二次方程[ax2+bx+c=0（a≠0）]的根和二次函數[y=ax2+bx+c（a≠0）]的圖像與[x]軸的交點的關系;（3）請歸納方程[f（x）=0]的根與函數[y=f（x）]的圖像與[x]軸的交點的關系.

（方程[f（x）=0]的根就是函數[y=f（x）]的圖像與[x]軸的交點的橫坐標.）

設計意圖：學生已了解二次函數圖像與方程根的關系，通過表格幫助學生梳理“三者”之間的關系，再提出一般問題. 三個問題從特殊到一般，從具體到抽象，滲透“從最簡單、最熟悉的問題入手解決較復雜的問題”的研究思路， 有利于培養學生的歸納能力和數學抽象素養.

3.抽象概括，形成概念

根據概念“對于函數[y=f（x）]，把使[f（x）=0]的實數[x]叫作函數[y=f（x）]的零點.”向學生闡明函數[y=f（x）]的零點問題就是方程 [f（x）=0]的根問題，零點的幾何意義就是函數圖像與[x]軸交點的橫坐標.在建立方程與函數聯系的過程中，“方程的根”是一個靜態的點，等價轉化為求“函數的零點”的動態過程，體現了“動”“靜”轉化的思想.

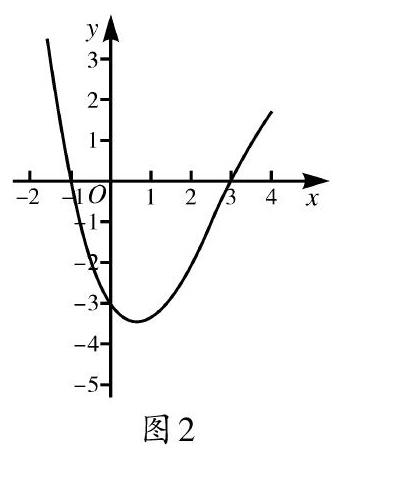
問題3：（1）觀察圖2，請寫出函數圖像與[x]軸交點的坐標及函數的零點;（2）函數的零點是點嗎？

設計意圖：從具體的二次函數到抽象函數的圖像，加深學生對函數零點概念的理解，明確“零點是交點的橫坐標，是一個實數，不是一個點，不能用交點的坐標表示”.

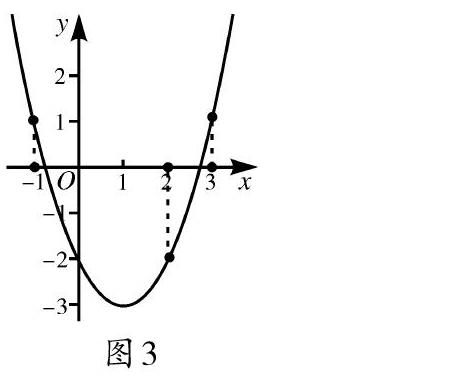
思考：在這些區間上，函數圖像有什么共同的特點？函數值的變化有什么共同點？

（3）已知函數[g（x）=x，-3≤x≤-1，-x2+2x+4，-1

引導學生概括：題（1）（2）的函數圖像是連續不斷的，圖像經過[x]軸，且在區間端點的函數值異號，函數有零點 .

題（3）在區間端點的函數值異號，但函數圖像（如圖5）是間斷的，從[-1]的左側到右側，函數值由負值直接跳到正值，即函數圖像沒有經過[x]軸，函數無零點.

師生共同提煉函數零點存在性定理：

如果函數[y=f（x）]在區間[[a，b]]上的圖像是連續不斷的一條曲線，并且有[f（a）·f（b）<0]，那么函數[y=f（x）]在區間[（a，b）]內有零點，即存在[c∈（a，b）]，使得[f（c）=0]，這個c也就是方程[f（x）=0]的根.

設計意圖：探究函數在區間[[a，b]]的端點函數值異號與零點存在性的關系，并通過題（3）強調圖像應是“連續不斷的一條曲線”，幫助學生將“圖像特征”轉化為“代數表示”，歸納出函數存在零點的條件.這個結論直觀簡潔，沒有證明，可作為定理直接運用.

5.定理辨析，深化理解

問題5：你能改變定理的條件或結論，得到新的命題嗎？請對你給出的命題判斷正誤，并畫草圖說明.

探究1（對換條件與結論）：如果函數[y=f（x）]在區間[[a，b]]上的圖像是連續不斷的一條曲線，且函數[y=f（x）]在區間[（a，b）] 內有零點，則[f（a）·f（b）<0] .