5～6歲兒童數學問題解決的認知診斷評估工具

李莉 周欣 涂冬波 高旭亮 黃瑾 楊志艷 李美芳 夏青

[摘 要] 基于認知診斷評估理論和技術，本研究采用文獻分析、專家研討和口語報告法構建5～6歲兒童“數與運算”領域數學問題解決的認知模型，對627名5～6歲兒童進行認知診斷評估，運用認知診斷模型—數據擬合對認知模型和診斷測驗進行質量檢驗。結果顯示，認知屬性對題目難度的解釋量為0.879，效應量為0.834，平均HCI為0.749;認知診斷測驗題目的平均區分度為0.707（標準差為0.299）;除兩題的題目擬合度S-X2指標的顯著性水平<0.01，其他題目的擬合度都較好;測驗的信度為0.95;平均掌握概率與測驗總分呈單調遞增曲線。以上結果說明，本研究構建的兒童數學問題解決認知模型良好，編制的認知診斷測驗具有較理想的測量信度與效度，可以作為評估兒童數學問題解決的有效工具，并可以提供精細豐富的診斷信息，從而為相關教育教學及干預研究提供科學依據。

[關鍵詞] 問題解決;數與運算;認知診斷評估

一、問題提出

學前兒童的數學學習與發展是基礎教育質量監測的重要方面，與未來學習乃至工作的關系密切。

研究表明，兒童在學前階段的數學知識和數學能力與小學階段的數學和閱讀成績密切相關，[1][2]能夠預測其在小學階段可能出現的數學學習困難，[3][4]在控制了家庭背景因素后，兒童入小學前的數學得分與大學學歷、今后的收入及經濟管理水平都有顯著相關。[5]同時，有研究表明，兒童早期數學學習的發展傾向于累計增長效應，[6]所以越早發現學前兒童在數學發展上的優勢和不足，越有利于兒童后期的數學學習與發展。

目前，美國、英國、澳大利亞等多個發達國家的兒童早期數學學習的培養標準或課程標準均體現出時代及社會對培養未來人才需求的變化，從掌握學科知識技能逐漸轉向培養綜合學習能力和素質。

如全美數學教師理事會提出，2～6歲兒童數學學習標準分為內容標準和過程性能力標準，前者包括數和數的運算、代數、幾何、測量、數據和概率，后者包括解決問題、推理和證明、交流、聯系和表征。英國威爾士政府在《學習型社會：基礎階段——3～7歲》（The Learning Country： The Foundation Phase—3 to 7 years）中指出，兒童數學發展包括利用和運用數學、計算和處理數據、測量、形狀和空間四部分，其中，利用和運用數學即引導兒童使用知識解決問題、進行數學交流和發展數學推理。澳大利亞早期學習（0～5歲）框架中，兒童的數學學習包括理解數字、數數、圖式、測量、空間意識、數據、數學思考和推理;其小學低年級（5～10歲）的數學標準包括數學課程內容和數學能力，前者包括數與代數、測量和幾何、統計和概率，后者包括理解、流暢、問題解決和推理。可見，各國都十分重視培養兒童綜合應對和解決問題的能力，而不是某方面單一的數學知識和技能。相對而言，我國《3～6歲兒童學習和發展指南》中，數學認知領域的結構維度較側重于數學內容，如數、數的關系和空間幾何，而解決問題、表達交流和表征等能力目標沒有作為單獨的維度凸顯出來。從實踐來看，我國幼兒園的數學教育長期以來一直關注數學知識的傳授，對兒童數學思維及問題解決能力的培養關注很少。

同時，我國幼兒園教師對傳授數學知識和判斷兒童數學知識的掌握比較熟悉，但對判斷和培養兒童的數學過程性能力缺乏經驗，在教育過程中也很少了解和記錄兒童過程性能力的表現，因此也很難充分促進兒童數學思維和數學應用能力的發展。有研究表明，我國幼兒園數學教育受到基礎教育數學課程改革的引導，教師能夠了解到《幼兒園教育指導綱要（試行）》和《3～6歲兒童學習和發展指南》中對引導兒童在實際生活中、在數學問題解決中學習數學的要求，但因為缺乏科學的手段去了解和評估兒童數學問題解決的水平和所需要的策略，無法給兒童提供適宜的游戲或活動來幫助兒童加深對數學知識的理解和應用。[7]因此，我國對學前兒童數學學習與發展的監測應加強評估兒童數學問題解決能力和數學知識應用能力，通過評估顯現出兒童在問題解決和數學應用能力上的優勢與不足，幫助教師了解兒童數學問題解決的發展水平，從而為幼兒園的數學教育實踐提供科學依據，實現數學知識和能力并重的培養目標。

由于基于標準測驗理論開發的學業成績或能力評估工具，往往只宏觀報告一個測評總分來代表個體的成績或能力，無法區分得分相同個體之間的個體差異，更無法報告測驗結果背后所隱藏的個體內部心理加工水平，即個體所使用的具體知識技能、加工策略或內在的認知結構，因此，測量理論進一步發展出了認知診斷評估（Cognitive Diagnosis Assessment，簡稱CDA）方法。CDA是以認知科學研究成果和現代心理計量學方法為基礎，對個體完成任務的認知過程、加工技能或知識結構進行診斷評估。[8]近年來，認知診斷理論與技術發展很快，國內已有的CDA研究中，80.85%為基礎研究，即理論介紹性文章和診斷方法研究，少部分為應用研究，[9]主要應用于評估小學三年級以上學生的數學或語言發展。[10][11][12][13][14]應用于學前教育階段以開發評估工具的研究尚為空白。為了從微觀層面了解學前兒童在數學問題解決上的優勢和弱勢，可以應用認知診斷的理論和技術開發測評工具，以滿足學前兒童數學學習與發展監測評估及幼兒園數學教育教學的需要。

另外，從上述兒童早期數學學習標準或課程標準可看出，學前階段的數學學習內容廣泛，主要包括數與運算、幾何空間、測量、統計與數據等內容，而數學問題解決需要以某一具體內容的數學問題為載體。以往研究表明，“數與運算”（number and arithmetic）是兒童數學學習的重要組成部分。[15]學前兒童的運算能力（arithmetic abilities）對一、二年級的運算成績有很強的預測作用。[16]學前兒童的數能力（number competence）能夠預測1～3年級的數學成績增長速度以及三年級的數學成績。[17]因此，本研究選擇以“數與運算”作為數學問題解決的載體，以5～6歲學前兒童作為研究對象，應用認知診斷的理論和技術，開發學前兒童數學問題解決的認知診斷測驗。

認知診斷測驗的開發過程如下：首先，分析兒童解決“數與運算”問題所需的認知屬性（cognitive attribute），并構建由這些認知屬性組成的認知模型（cognitive model）;然后，以具體測驗題目為載體，提出測驗題目及評分與認知屬性之間的假設，確定測驗Q矩陣，編制測驗，開展測評;最后，選擇合適的認知診斷模型，與測評的實際數據進行擬合，分析測驗的題目特征和作答反應的關系，檢驗認知模型及認知診斷測驗的質量。

二、5～6歲兒童數學問題解決認知模型構建

構建認知模型首先需要對兒童解決“數與運算”任務時用到的知識、技能和認知加工過程進行分析，探明影響5～6歲兒童完成這些任務的核心認知屬性，這是開發CDA的關鍵步驟。認知屬性是指完成測驗任務所涉及的知識結構或認知加工技能，[18]應符合四個基本特征：屬性粒度的合適性、屬性的可測性、屬性與教學的相關性和屬性的順序性。[19]確定認知屬性和屬性之間的關系即構建認知模型的過程，常用方法有文獻回顧法、專家任務分析法和口語報告法。[20]

（一）文獻回顧初步確定認知屬性

1. 回顧與數學問題解決的認知加工過程及影響因素有關的研究文獻。

第一，國內外心理學領域對問題解決的研究主要從信息加工理論探討問題解決的外在過程和內在機制，雖結論不盡相同，但也體現出很多共識，即數學問題解決的過程包括四個基本環節：問題感知及表征、選擇解決方案、執行解決方案和對結果的反思和檢驗。[21][22][23][24][25][26]這幾個環節只是人為的劃分，在實際解決問題的過程中是無法完全割裂開來的，彼此滲透又循環往復，直至解決問題。在問題感知和表征階段，個體嘗試理解問題情境中的已知條件和需要達到的目標，形成自己對問題的理解，并用數學語言對問題進行再加工;進而將當前問題與已有的數學知識和經驗相聯系，歸類到某一數學問題的類型，從而選擇一個解決此類型數學問題的解決方案;然后嘗試執行此方案看是否可以解決問題，在執行的過程中需要執行功能和推理與驗證等過程性能力的參與;如果沒有解決問題，個體會重新理解和表征問題，選擇下一個解決方案進行嘗試;每個環節都伴隨著個體對這個環節產出結果的反思和檢驗，直至認為達到問題解決的目標。

第二，已有數學問題解決的研究多以口頭或書面形式的數學應用題（word problems）作為問題呈現，特別是小學低年級和學前兒童，往往采用口頭應用題形式。已有研究按照數學問題呈現的語義結構（semantic structure）將加減應用題的問題類型分為三種：合并型語義題、變化型語義題和比較型語義題。其中，變化型語義包含三個子類：結果未知型、變化未知型和初始未知型。比較型語義包含兩個子類：一致型比較和非一致型比較。[27][28][29]以往研究對兒童解決合并型和變化型語義題的難易程度結果并不一致，但普遍認為兒童解決比較型語義題最為困難。有研究表明，小學一年級和學前兒童在變化問題解決上的表現較好，在比較型問題解決上較差，[30]在變化型子類問題解決上，兒童解決結果未知型問題成績最好，初始未知型表現最弱;在比較型子類問題解決上，兒童解決非一致型比較更為困難。[31][32]

第三，對兒童解決數學應用題的內在機制的研究主要有兩種理論模型：數學知識應用模型和語言理解模型。[33]數學知識應用模型強調數學知識在問題解決中的重要角色，即兒童在解讀問題后，啟動運算知識或數的知識來解決問題。語言理解模型則從語言理解的角度描述兒童的解題行為，即兒童在解讀問題后，啟動文本庫和問題模型來解決問題。

第四，已有研究采用認知診斷評估開發數學問題解決的認知診斷測驗，[34][35][36]這些研究采用的認知診斷模型主要包含兩個認知成分：數學知識成分和認知過程成分（或認知加工成分）。數學知識成分包括的認知屬性是與診斷的具體內容相關的數學知識或技能。如，診斷運算技能，數學知識成分包括基本算術運算、多步運算等。認知過程成分包括的認知屬性多是與問題解決本身有關的加工過程。如，語義表征（識別有效條件，提出問題），識別隱含條件，關系表證（分析數量關系，問題和條件之間的關系），選擇算法等。

以上這些研究為本研究確定認知屬性提供了支持和借鑒：（1）數學問題解決的普遍過程及內在

機制為：問題識別與表征（認知成分：已了解和掌握的數學語言和符號，數的知識或運算的知識）—選擇解題策略（認知成分：已有經驗中的問題類型）—執行解題策略（認知成分：執行功能、推理與驗證等）—結果的反思和檢驗（認知成分：元認知、推理與驗證等），可以在此基礎上進一步了解學前兒童數學問題解決的具體特點。（2）兩種理論模型雖然視角不同，但都沒有否定彼此的作用，因此，在構建認知模型時應同時關注數學知識和語義類型對兒童數學問題解決的影響。（3）可以借鑒已有的數學問題解決認知診斷測驗中對認知屬性的界定。但由于這些研究都是以小學中高年級兒童作為研究對象，仍需篩選和挖掘與學前兒童數學問題解決相關的認知屬性。

2. 回顧與兒童早期數學學習與發展相關的研究文獻，以析出與5～6歲兒童“數與運算”問題解決相關的具體數學知識成分和過程性能力成分。

首先，從兒童早期“數與運算”發展軌跡的研究可知，5～6歲兒童基本已掌握基數概念，能使用計數策略進行集合比較，70%以上（城市）兒童能夠解決10以內加減口頭應用題。[37][38][39]因此，對于5～6歲兒童數學問題解決所使用的數學知識成分而言，主要包括基數概念、集合比較和10以內加減運算。

其次，從各國兒童早期數學發展標準來看，兒童早期數學學習除了要求掌握基礎數學知識外，更側重于引導兒童的數學思維和應用數學等過程性能力。兒童數學問題解決所涉及的過程性能力主要包括數學交流、數學表征、數學關聯和數學推理與驗證四個要素。[40]數學交流表現為能夠使用數學語言表達自己的數學思維和理解他人的數學思維;數學表征表現為能夠使用某種具體或抽象的形式，如數學符號、圖表等處理數學概念或數學關系，并能夠在解題過程中靈活轉換表征方式;數學關聯表現為能夠利用數學知識觀念之間的聯系以及數學與其他學科之間的聯系來解決數學以外情境中的問題;數學推理與驗證表現為能夠提出數學設想，并通過證明或反例驗證自己的設想。其中，數學推理包括數量推理和其他推理（如空間推理），算術應用題中應用到的多是數量推理。實證研究表明，與算術技能相比，兒童的數量推理能力（包括對加法組合、加減逆反關系、部分—整體關系和一多對應關系的理解）對5年后的數學成績有更強的預測。[41]

通過對以上兩部分文獻的回顧，初步確定5～6歲兒童數學問題解決的認知成分包括數學知識、過程性能力和語義理解三部分。其中，數學知識成分包括基數概念、集合比較、10以內加法和10以內減法。語義理解成分包括合并型、變化型和比較型三種語義題。過程性能力包括數學交流、數學表征、數學關聯和數學推理與驗證。

（二）專家研討再次確定認知屬性及其層級關系

從文獻回顧初步析出構建認知模型所需要的認知成分后，需要確定每類認知成分具體包括的認知屬性及其層級關系，因此，本研究邀請學前教育領域專家（3名）、學前教育專業博士生（3名）、幼兒園特級教師（2名）和骨干教師（2名），及測量學專家（2名）組成研討團隊開展頭腦風暴。先由測量學專家對研討小組成員進行認知診斷理論和技術的培訓，使其了解良好認知屬性的特征（主要是粒度大小適宜、可測性和明確的層級關系）;然后專家組對文獻回顧析出的認知成分逐一進行分析，確定最終可以使用的認知屬性;最后，對最終確定的認知屬性進行描述、界定和編碼。

由于文獻回顧均為實證研究，專家組對認知成分及其層級關系的認同度較高，主要的爭議在于屬性粒度的大小、可測性和屬性的數量多少上。第一，5～6歲兒童在解決算術應用題時主要涉及的數學知識是運算技能，是否有必要加入基數概念和集合比較？大多數專家表示，雖然這兩項知識和技能是幼兒園小、中班教育內容，大多數兒童在5歲前基本掌握，但不排除數學學習困難的兒童仍未掌握。更重要的是，有些推理性較強的數學問題可能不一定用到運算技能，但需要用到基數概念和集合比較的知識，如加法組合推理類的題目。如果沒有納入這兩項認知屬性，就無法全面的診斷兒童解題錯誤的根本原因。因此，數學知識成分中包括基數概念和集合比較。第二，10以內加法和10以內減法是兩個認知屬性還是合并為10以內加減運算這一個認知屬性？最初，專家們希望能夠區分加法和減法，以便更好地診斷出兒童在加法和減法應用題上的優劣。但鑒于兒童解決數學應用題時策略是靈活的，并不能確定是采用了加法還是減法，無法實現對測驗題目所考查認知屬性的準確標定，因此，最終確定10以內加減運算為一個認知屬性。第三，數學應用題所包含的語義類型選擇哪些？加減應用題的語義類型一共有6種，再加上其他兩個認知成分所包含的認知屬性，數量較多，大大提高了編制認知診斷測驗的難度，也會影響數據—模型擬合的效果。鑒于以往實證研究結果，兒童對初始未知的變化型語義題理解有較大難度，因此不納入此次考查范圍，只保留其他5種語義題型。第四，認知診斷測驗可以實現對哪些過程性能力的考查？測量專家從認知診斷技術的角度建議，兒童解決每道題目都可能用到的能力無法在題目標定時進行區分，不適合作為認知屬性，如數學表征和數學交流，測量難度較大的屬性很難開發測驗題目，如數學關聯。專家們一致表示，認知診斷測驗只是評估兒童數學學習與發展的工具之一，有些過程性能力更適合教師在日常觀察中進行記錄，不需要在認知診斷測驗中面面俱到。對于加減運算應用題而言，數量推理是較為關鍵的認知屬性，最終確定僅考查數量推理一項過程性能力。另外，由于數量推理中對整體—部分的理解與合并型語義和結果未知的變化型語義有一定程度的重復，采用的應用題目基本一致，因此，只保留加法組合推理、加減逆反推理和一對多推理作為數量推理的認知屬性。

經專家研討，最終確定了5～6歲兒童“數與運算”問題解決的認知模型（如圖1所示），包括3個認知成分和11個認知屬性（具體名稱及描述見表1），它們之間的層級關系屬于分支型，[42]其中，A1是除了A6和A8外其他所有屬性的先決條件，A5是A6的先決條件，A7是A8的先決條件。先決條件也被稱為先決屬性。如果屬性A是屬性B的先決條件，即被試除非先掌握屬性A，否則無法掌握屬性B，則屬性A為屬性B的先決條件。

（三）兒童口語報告的質性驗證

口語報告法是通過要求被試報告問題解決過程中頭腦的思維過程來識別問題解決所需的認知信息和加工技能。由于幼兒元認知、反思及表達能力有限，本研究以兒童口語報告為主，輔以主試觀察記錄，考察兒童數學問題解決的過程及背后的認知成分。

首先，根據上面確定的認知模型編制了25道數學應用題。然后，采用目的性抽樣，[43]從上海市兩所示范園的大班各選取3名兒童進行口語報告。選擇的條件是：（1）以教師日常觀察的經驗，選擇在數學活動中的表現為好、中、弱的兒童各一名;（2）所選擇的兒童愿意參與數學活動，能夠基本表達出自己解題時想了什么及如何得出答案的過程。采用一對一測查的方式，將數學應用題口述給兒童，觀察兒童在解題過程中的表現，并在解題后詢問解題的過程。通過對6名兒童口語報告和觀察記錄的分析，可以發現，5～6歲兒童解決數學問題的過程遵循數學問題解決的普遍性過程，即對問題進行理解—歸類為加法問題或減法問題—選擇加法或減法策略—得出結論。不同的是，此年齡段的兒童大多缺乏對結果的反思和檢驗。在對問題進行理解時，首先，應用以往的數學知識和經驗，提取出題目中的數字或數量信息，然后將其歸類為語義類型和推理類型，從而做出選擇加法或減法的解題策略。同時，是否能夠得出正確答案也依賴于兒童對運算技能的掌握。因此，通過兒童的口語報告，我們可以發現，5～6歲兒童解決“數與運算”問題至少需要掌握一定的運算技能，同時能夠理解語義類型和數量推理類型。

另外，還發現：（1）因為是口頭應用題形式，兒童的執行功能會對問題解決有影響，但執行功能是兒童解決問題必備的一般認知能力，并不是認知診斷測查的認知屬性，因此，需要在編制測驗和實施測查的過程中盡量降低執行功能對問題解決的影響。（2）認知屬性之間的相互作用在不同題目上有不同的反映機制。如作答合并語義理解的題目，必須同時掌握A3和A4屬性，否則無法解決問題。而作答加減逆反推理的題目，A3和A9屬性之間就具有補償關系。因此，需要在編制測驗時謹慎處理題目的屬性標定及評分，并在模型—數據擬合時采用相對擬合檢驗。（3）兒童在同一道問題上可能采用不同的策略來解決，如，變化未知的應用題，既可以采用加法，也可以采用減法來解決。而策略與認知屬性既有關系又相互獨立，可在測查過程中單獨記錄。這些發現為編制認知診斷測驗和選擇認知診斷模型提供了參考依據。

三、編制認知診斷測驗

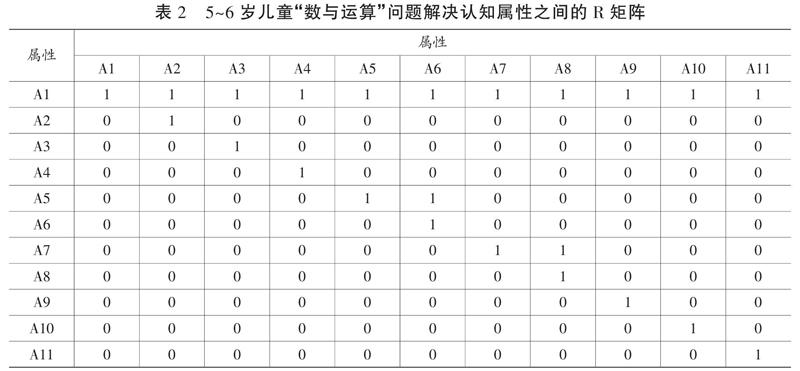
（一）基于認知模型得到R矩陣

基于屬性層級關系可以得到屬性之間的直接和間接關系，用0表示屬性之間沒有直接關系，1表示屬性之間有直接或間接的關系，從而形成元素為0或1的可達矩陣，即R矩陣（見表2）。R矩陣是實現對每個屬性準確診斷的前提條件。[44]

（二）基于R矩陣得到測驗Q矩陣

首先，基于R矩陣通過縮減法、擴張算法或漸進式擴張算法[45]可以得到11個認知屬性所組成的所有潛在知識狀態（knowledge states），形成被試Q矩陣（也稱為理想掌握模式，0表示被試掌握了某認知屬性，1表示被試沒有掌握某認知屬性），共577種，表示被試對認知屬性的所有潛在掌握模式。刪除理想掌握模式中11個認知屬性全為0的模式，得到566種理想測量模式，表示題目與認知屬性之間的關系（0表示此題目不考查某認知屬性，1表示此題目考查某認知屬性）。然后，根據認知診斷測驗編制的原則（如Q矩陣包含R矩陣）以及考慮5～6歲兒童生理心理特點對測試題量的限制，最終選擇其中的30種測量模式作為測驗Q矩陣，即編制測驗依據的測量模式。

（三）編制認知診斷測驗

編題過程中，R矩陣中有五種測量模式（10001100000、10000011000、10000000100、10000000010和10000000001）因編題專家難以命題而舍棄，最終剩下25種測量模式。同時，為保證對每種認知屬性至少測量3次，會設計不同題目重復考查某一測量模式。最終形成38道題目的《5～6歲兒童數學問題解決認知診斷測驗》（其Q矩陣舉例詳見表3）。通過對30名兒童的試測，測驗的考查時間在25分鐘左右。

測驗題目方面，僅測量A1的題目采用按數取物任務，僅測量A1A2的題目采用隨機排列集合比較任務，僅測量A1A3的題目采用口頭算術題，其他題目均采用口頭應用題形式。計分采用0～1計分，0表示兒童至少沒有掌握該題目考查的其中一種認知屬性，1表示兒童掌握了該題目考查的所有認知屬性。由于兒童答對題目所采用的策略是多樣的，也會包括猜測策略，為保證評分確實能夠反映出兒童對該題目所考查認知屬性的掌握情況，會對兒童的答題過程進行記錄和詢問，判斷兒童使用的解題策略是為考查的認知屬性服務時才計為1分。

另外，為了保證測驗題目僅測查這11個認知屬性，在設計題目時特別注意降低其他因素（執行功能、生活經驗差異和應用題的語言表述）的影響，如控制應用題的長度，較長的題目借助圖片幫助兒童記憶，采用貼近兒童日常生活的問題情境和貼近兒童理解的語言表述，復述兩遍題目等。

（四）認知診斷測驗的計分說明

認知診斷測驗雖然采用0～1計分，但與傳統測驗相比，并非按照兒童回答答案的對錯進行0～1計分，而是按照兒童是否掌握每道題考查的認知屬性來進行計分，只有當兒童掌握了該題目考查的所有認知屬性時才能計為1分，否則計為0分。下面通過舉例來說明認知診斷測驗的計分依據及過程。

1. 認知診斷測驗的計分過程。

第12題“你拿著7張玩具卡片玩游戲，先是贏了5張，后來又輸了5張，現在你有幾張玩具卡片呢？為什么呢？”，屬性標定為A1A5A9。

此題考查的是兒童對基數概念（A1）、理解結果未知的變化語義（A5）和加減逆反推理（A9）的掌握情況，不包括對加減運算（A3）的掌握情況，因此，當兒童使用加減逆反推理（如，觀察到反應時很短，很快回答7張，兒童可能沒有使用運算，而是利用對加減逆反關系的理解推理出答案，再輔以兒童對“為什么”的回答，如“贏了又輸了等于還是原來的卡片”，再次確定兒童使用的解題策略）解決問題時才計為1分;如果兒童的回答是因為7+5=12，12-5=7，所以現在有7張卡片（此后會詢問兒童是否還有其他辦法，如表示沒有，則定為A3策略），或表達算不出，或觀察到停滯在運算過程算不出，皆為0分。

2. 需要記錄計分與認知屬性掌握情況的對應依據。

第17題“哥哥有7顆草莓，哥哥比妹妹少3顆草莓，妹妹有多少草莓呢？”，屬性標定為A1A3A7A8。

此題考查的是兒童對基數概念、加減運算、一致型比較和非一致型比較語義理解的掌握。當兒童回答是10，計為1分，并且解題的過程是采用7+3是10或10少3個是7，才能表明兒童理解了非一致型比較語義，采用了正確的加減解題策略，并掌握了加減運算知識，保證計算的正確性。當兒童的答案為非10的數字，計為0分時，兒童沒有掌握的認知屬性可能并非一樣。如果兒童回答是4顆，因為7-3是4，表明兒童沒有掌握非一致型比較語義理解但掌握了運算知識;或回答是9顆，因為7+3是9，表明兒童沒有掌握加減運算但理解了非一致型比較語義。

四、認知模型及認知診斷測驗的質量檢驗

（一）測試對象

采用分層取樣和方便取樣的方法，從上海市六個區（長寧區、黃浦區、靜安區、楊浦區、浦東新區、寶山區）抽取示范園、一級園和二級園共16所，大班兒童計627人，平均年齡67.69個月（標準差3.78）。其中，男生294人，女生333人;示范園112人，一級園393人，二級園122人。

（二）測試材料

采用自編《5～6歲兒童數學問題解決認知診斷測驗》，共計38道題目，采用0～1計分。

（三）分析方法

首先，檢驗屬性及屬性層級關系的可靠性。具體方法：一方面，采用回歸分析的統計方法，通過建立題目難度對認知屬性的多元線性回歸，考察認知屬性對題目難度的解釋力。如果認知屬性能夠解釋題目難度的60%以上，則說明確定的認知屬性基本可靠。[46]另一方面，采用HCI指標驗證屬性間的層級關系。

其次，采用模型—數據擬合檢驗方法檢驗測驗題目的參數估計及測驗的有效性。首先，采用相對擬合檢驗，即比較多個認知診斷模型對同一批數據的擬合情況，選擇相對擬合最優的診斷模型。本研究選用五種常用認知診斷模型進行比較，分別是：DINA模型（Deterministic inputs， noisy “and”gate），[47]RRUM模型（Reduced reparametrized unified model），[48]DINO模型（Deterministic inputs， noisy “or”），[49]LLM模型（Linear Logistic model）[50]和G-DINA模型（Generalized deterministic inputs noisy“and”gate）。[51]采用的擬合指標包括：偏差（deviance，-2*Log-Likelihood，-2LL）、AIC 以及 BIC，這些指標值越小說明模型與數據擬合越好。然后，使用CDM 包進行參數估計，包括題目區分度指標，[52]題目絕對擬合指標S-X2值[53][54]和屬性重測一致性信度指標。[55]第三，采用最大后驗估計方法（Maximum A Posterior Estimation， MAP）估計被試的屬性掌握概率，分析被試總分與屬性掌握概率之間的關系，從而考察診斷評估的有效性。

（四）分析工具

使用Excel 2007進行基本數據處理;使用SPSS23.0進行描述性統計、方差分析和回歸分析;使用flexMIRT分析題目難度;使用CDM包（Version 4.6-0）[56]進行認知診斷分析。

（五）研究結果

1. 認知屬性及層級關系的分析結果。

首先，考察認知屬性對題目難度的解釋力。5～6歲兒童數學問題解決認知診斷測驗所考察的11個認知屬性對題目難度的解釋量為0.879，效應量為0.834（見表4）。解釋力遠高于60%，可見確定的認知屬性充分可靠，能夠很好地預測題目難度。

其次，通過HCI指標驗證屬性層級關系。HCI的取值為[-1，1]，1表示完全擬合，-1表示完全不擬合，一般0.70左右表示很好的模型—數據擬合。[57]結果顯示，測驗平均HCI為0.749，說明屬性層級關系的模型—數據擬合情況良好，測驗Q矩陣良好。

2. 測驗題目特征分析及整體測驗質量分析。

首先，選擇最合適的認知診斷模型。所選5種模型的測驗擬合指標（見表5）顯示：對于-2LL而言，GDINA是擬合最優的模型。因為GDINA是飽和模型，與簡約模型（DINA、rRUM、DINO和LLM）相比，-2LL總是傾向于選擇飽和模型。[58]對于AIC和BIC而言，LLM是擬合最優的模型。因此，本研究選用LLM模型進行模型—數據擬合分析。

第二，使用CDM包進行測驗參數估計。結果顯示：（1）除了題目1、2、7和10的區分度低于0.20外，所有題目的區分度在0.211～0.989之間，平均區分度為0.707（標準差為0.299），說明測驗整體的區分度較高，質量較好。（2）除了題目23和28的題目擬合度S-X2指標的P<0.01外，其他題目的擬合度都較好。（3）各屬性的信度取值為0.89～0.99，平均信度為0.95。（見表6）

第三，測驗的有效性分析。采用測驗總分與屬性掌握概率之間的關系分析，結果呈現單調遞增趨勢（如圖2所示），說明能力越強，屬性掌握概率越高，即測驗的結果是有效的。

3. 被試掌握模式分析。

采用最大后驗估計方法（Maximum A Posterior Estimation， MAP）來估計被試的屬性掌握模式。本研究共測查627名被試，共得到110種屬性掌握模式，超過半數被試的屬性掌握模式集中在16種模式中（見表7）。其中，所有屬性都沒有掌握（00000000000）的人數達到10%，只掌握數學知識成分（10000000000、11000000000、10100000000、11100000000）的人數占25.8%，這兩種情況達到了三分之一以上的人數。掌握一個及以上語義理解成分且沒有掌握數量推理成分（不考慮數學知識成分）的人數占12.7%，掌握一個及以上數量推理屬性的人數（不考慮其他屬性）占1.4%。所有屬性都掌握（11111111111）的人數占比非常小。

五、討論

本研究旨在編制5～6歲兒童“數與運算”問題解決的認知診斷工具，為更精細地了解兒童數學學習的優勢和不足提供了豐富信息，為因材施教和補救干預提供了科學依據，具有較強理論和應用價值。

（一）數學知識、語義理解和數量推理對于數學問題解決來說是相輔相成的

本研究通過文獻分析、專家研討和口語報告法構建5～6歲兒童數學問題解決認知模型，共計3種認知成分和11個認知屬性，共同解釋了題目難度的87.9%，HCI值在0.7以上，表明本研究建構的認知模型比較理想。從構建模型的層級關系來看，運算、語義理解和數量推理是平行結構，說明三者對兒童能夠成功解決數學問題都很重要，并不能因為強調某一方面而忽視了另一方面，而應該相互交融共同發展。

目前的幼兒園數學教育多側重數學知識的教學，即讓幼兒記憶各種數學事實，包括口頭和書面數字、數字線和加減運算等。當解決情境性問題時，兒童不知道選擇何種數學知識或策略，可能會出現機械應用的情況。如，考查比較型語義理解的題目，不少兒童聽到“多”就采用加法，聽到“少”就采用減法;考查數量推理的題目，也有些兒童一聽到數字就開始加或減，并沒有真正思考數字代表的集合之間的關系以及數字發生的變化之間是何關系。這些都反映出幼兒園數學教育缺乏引導兒童在解決問題中學習數學，缺乏通過應用數學加深對數學知識的理解和遷移。當然，數學知識是應用數學解決問題的基礎，理解了語義開始解決問題時，如果運算不對，也無法得到準確的答案。所以，數學知識、語義理解和數量推理三者是相輔相成、相互成就的。

同時，數學問題是問題解決認知診斷測驗的依托。有研究者認為數學問題解決中的問題，并不包括常規數學問題，而是指非常規數學問題和數學應用題。[59]因為學生解決常規問題可以依賴記憶，而解決CUN問題（complex，unfamiliar，non-routine problem）需要的是直覺、數感和邏輯推理。[60]也有研究建議考察兒童早期的問題解決可以同時使用常規問題和非常規問題。[61][62]由于本研究構建的認知模型既包括對數學知識的考查，也包括對數量關系理解和推理的考查，因此，對于數學知識的考查，采用算術表達式或口頭算術題這類常規數學問題，兒童通過從長時記憶中回憶數學事實就可以解決問題。而對數量關系的理解和推理的考查則采用非常規問題，雖然正確答案是唯一的，但解決這類問題的策略是多樣的，兒童無法通過回憶數學事實來解決問題，需要通過調動已有的經驗，進行數學思考和推理來解決問題。本研究開發的認知診斷測驗中，僅8道題為常規問題，如“3加上5是多少”，或“你有5個蘋果，媽媽又給了你3個蘋果，你現在的蘋果是變多了還是變少了呢？”，用于考查單一數學知識成分或語義理解成分;其他均為非常規問題，如“公交車上有6個人，到站之后下去了2個人，又上來了3個人，現在公交車上有幾個人呢？”，[63]用于考查綜合使用運算、語義理解和數量推理成分來解決問題。當然，相同的題目，對于不同數學能力水平的幼兒來說，數學問題的類型并不是固定的。比如，對于達到心算水平的幼兒來說，在回答加減口頭算術題時，可直接從記憶中提取現成答案，算是解決常規問題，但對于尚未達到心算水平幼兒來說，頭腦中并不存在現成的答案，他們會借助積木或手指探索出問題的答案，對他們而言，又是非常規問題。

（二）多種方法檢驗認知診斷測驗的質量

首先，采用相對擬合檢驗有利于選擇最優模型。認知診斷測驗要得到準確的診斷結果，必須確保用于測驗質量分析的認知診斷模型能夠精確地反映被試作答反應與認知成分之間的各種關系，如，多個屬性在被試作答時是如何發揮作用的，題目作答是否有多種策略等。本研究在兒童口語報告過程中發現，由于認知屬性較多，關系較為復雜，兒童在解決考察多屬性題目時，多個屬性之間有可能是補償關系，也有可能是非補償關系，因題而異。因此，本研究采用5種認知診斷模型比較的方法，確定最合適的模型，保證所選模型能夠更好適用于作答數據，從而更科學有效地驗證測驗的質量。

第二，通過區分度、題目擬合度、信度和被試屬性掌握概率與作答分數的關系等多種指標和方法檢驗認知測驗的測量學指標。從區分度指標來看，測驗整體的區分度較高（平均區分度為0.707），質量較好。雖然題目1、2、7和10的區分度低于0.20，但這四個題目均為R矩陣測量模式，考慮保留。其中，題目1和2的測量模式相同（10000000000），分別是5以內基數和10以內基數概念，相對于大班兒童難度較低，也許是導致區分度較低的原因，可以考慮刪去題目1。從題目擬合度S-X2指標的P值來看，題目23和28的題目擬合度不太好。可能與題目的情境、兒童的經驗及評分有關，可以考慮刪除。另外，屬性及測驗整體信度較高;測驗總分與屬性掌握概率之間呈現單調遞增趨勢，說明測驗的結果是有效的。以上結果均顯示本研究所建構的兒童數學問題解決認知模型和編制的認知診斷測驗具有良好的測量學指標，可以刪除題目1、23和28后形成正式的測驗。

第三，從認知診斷評估的結果檢驗認知診斷效果。從研究結果可發現：（1）診斷的三種成分中，被試對數學知識掌握最好，而且只掌握數學知識成分人數占被試總數25.8%。這與以往數學教育重知識輕能力的現狀也比較吻合。（2）在語義理解成分中，被試對變化未知和非一致型比較的語義理解掌握較弱，也得到以往研究文獻支撐。兒童在解決變化未知應用題和不一致型比較應用題時更加困難。[64][65][66][67]（3）在數量推理成分中，被試對加減逆反推理的掌握最弱。雖然有研究認為5～6歲是兒童掌握和運用加減反演律快速發展時期，[68]但僅有32.8%的5歲兒童在加減逆反問題上獲得成功。[69]數量推理的三種類型中，兒童對一多對應的關系理解建立在對一一對應的關系理解之上，后者的發展始于數數技能，因此兒童可借鑒數數策略而非運算策略來解決一多對應問題，降低問題解決的難度。兒童對加法組合的理解主要建立在對量詞的理解上，對邏輯思維的要求較小。相比較而言，對加減逆反推理的理解最為抽象，特別是對加減逆反變式的理解更為困難，兒童傾向于直接采用運算策略，而非邏輯推理，甚至越為熟練的運算技能反而會阻礙兒童去思考數量加減變化時的逆反邏輯關系。

（三）研究局限

本研究應用認知診斷方法，嘗試探索和開發學前兒童數學問題解決認知診斷評估工具，研究中存在一些局限。首先，本研究的認知屬性較多，但樣本偏小，可能不足以反映出更多的被試掌握模式。因此，還需增加樣本量，提高參數估計精度。其次，雖然本研究選擇了五個認知診斷模型，但有可能還有其他在假設上更貼近本測驗的模型，有待測量專家進一步驗證。第三，由于編制測驗題目的難度較大，導致測驗Q矩陣并沒有完全包括R矩陣，可能會影響模型—數據擬合。第四，由于測查方式采用一對一測查口頭應用題，難免受到兒童執行功能和學習品質水平的影響，可能會影響測量的精度。

六、結語

本研究構建了5～6歲兒童“數與運算”問題解決的認知模型，并在此基礎上編制5～6歲兒童數學問題解決的認知診斷測驗。該測驗具有良好的區分度和信效度，可以作為評估兒童數學問題解決的有效工具。對教育實踐來說，教育評估既是指揮棒也是顯示器。本研究通過開發學前兒童數學發展的評估工具，一方面旨在引導幼兒園的數學教育兩手都要抓兩手都要硬，不僅要重視數學知識的啟蒙與教育，也要探索如何激發兒童的數學思維，培養兒童數學問題解決的能力;激發幼兒園教師在傳授數學知識的同時，創設多種問題情境及語言表述方式，激發兒童應用所學的數學知識，達成數學知識的遷移和應用，同時對數學教育時機保持敏感，捕捉各種教育機會，讓數學知識滲透在日常問題解決中，通過解決問題深化知識的學習，加深數學語言的理解和交流。另一方面旨在為幼兒園教師提供科學的工具，幫助其更好地了解兒童對數學知識的掌握情況，了解兒童對數學問題的語義理解和數量推理方面的優勢和不足。比如，通過測試教師可以發現，有些孩子算術題已經達到心算水平，但問其“有10個小朋友參加拍皮球活動，老師拿來了4個皮球，還需要幾個皮球呢”，兒童一臉茫然，不知道是用加法還是減法來解決這個問題。而有些孩子非常明白如何解決一個問題，但總也算不對。這個評估工具可以讓教師從微觀層面看到兒童的個體差異，為后續的因材施教提供診斷性信息，從而真正促進兒童的數學發展。

致謝：感謝參與認知模型建構的所有專家和教師，感謝支持調研的所有園長和大班教師以及參與調研的所有大班兒童，感謝參與收集數據的各位同學。

參考文獻：

[1]GEARY D C. Mathematics and learning disabilities[J]. Journal of Learning Disabilities，2004，37（1）：4-15.

[2]DUNCAN G J， DOWSETT C J， CLAESSENS A， et al. School readiness and later achievement [J]. Developmental Psychology，2007，43（6）：1428-1446.

[3]JORDAN N C， KAPLAN D， LOCUNIAK M N， et al. Predicting first-grade math achievement from developmental number sense trajectories[J]. Learning Disabilities Research & Practice，2007，22（1）：36-46.

[4]STOCK P， DESOETE A， ROEYERS H. Detecting children with arithmetic disabilities from kindergarten： evidence from a 3-year longitudinal study on the role of preparatory arithmetic abilities[J]. Journal of Learning Disabilities，2010，43（3）：250-268.

[5]CHETTY R， FRIEDMAN J N， HILGER N， et al. $320，000 kindergarten teachers[J]. Phi Delta Kappan，2010（92）：22-25.

[6]MORGAN P L， FARKAS G， WU Q. Kindergarten childrens growth trajectories in reading and mathematics： who falls increasingly behind[J]. Journal of Learning Disabilities，2011（5）：472-488.

[7][37]許曉暉.兒童早期日常數學問題解決能力發展及其影響因素研究[D].北京：北京師范大學， 2005：4-5.

[8][18]LEIGHTON J P， GIERL M J. Cognitive diagnostic assessment for education[M]. Cambridge：?Cambridge University Press，2007：3，88-99.

[9]戴海琦，謝美華，丁樹良.我國大陸認知診斷研究的文獻計量分析[J].南京師大學報（社會科學版），2013（6）：88-97.

[10]李峰，余娜，辛濤.小學四、五年級數學診斷性測驗的編制：基于規則空間模型的方法[J]. 心理發展與教育，2009（3）：113-118.

[11][34]涂冬波，戴海崎，蔡艷，等.小學兒童數學問題解決認知診斷[J].心理科學，2010，33（6）：1461-1466.

[12][35]康春花，辛濤，田偉.小學數學應用題認知診斷測驗編制及效度驗證[J].考試研究，2013（6）： 24-43.

[13]康春花，吳會云，陳婧，等.小學數學“圖形與幾何”認知診斷測驗的編制[J].教育測量與評價： 理論版，2015（10）：4-8， 28.

[14]范曉玲，王珺，周路平，等.基于規則空間模型的3～4年級閱讀障礙兒童語素意識的認知診斷[J].教育測量與評價，2017（5）：12-16.

[15]SARAMA J， CLEMENTS D H. Early childhood mathematics education research：learning trajectories for young children[M]. New York and London： Routledge，2009：27.

[16]STOCK P， DESOETE A， ROEYERS H. Predicting arithmetic abilities： the role of preparatory arithmetic markers and intelligence[J]. Journal of Psychoeducational Assessment，2009，27（3）：237-251.

[17]JORDAN N C， KAPLAN D， RAMINENI C， et al. Early math matters： kindergarten number competence and later mathematics outcomes[J]. Developmental Psychology，2009，45（3）：850-867.

[19]GIERL M J， ROBERTS M， ALVES C， et al. Using judgments from content specialists to develop cognitive models for diagnostic assessments[A]. The annual meeting of the National Council on Measurement in Education. San Diego， CA. USA，2009.

[20][46]涂冬波，漆書青，戴海琦，等.教育考試中的認知診斷評估[J].考試研究，2008（4）：4-15.

[21]MAYER R E. Thinking， problem solving， cognition（2nd ed.）[M]. New York： W. H. Freeman and Company，1992.

[22]喻平.數學問題解決認知模式及教學理論研究[D].南京：南京師范大學，2002：21-23.

[23]LUCANGELI D， TRESSOLDI P E， CENDRON M. Cognitive and metacognitive abilities involved in the solution of mathematical word problems： validation of a comprehensive model[J]. Contemporary Educational Psychology，1998，23（3）：257-275.

[24]DEEK F P， TUROFF M， MCHUGH J A. A common model for problem solving and program development[J]. IEEE Transactions on Education，1999，42（4）：331-336.

[25]梁好翠.論數學應用問題解決的認知過程模式[J].欽州學院學報，2008（6）：107-111.

[26]魏雪峰，崔光佐.小學數學問題解決認知模型研究[J].電化教育研究，2012（11）：79-85.

[27]CARPENTER T P， MOSER J M. The development of addition and subtraction problem-solving skill[C]//CARPENTER T P， MOSER J M， ROMBERG T A. Addition and subtraction： a cognitive perspective. Hillsdale， NJ： Lawrence Erlbaum Associates Inc，1982：9-24.

[28]HELLER J I， GREENO J G. Semantic processing of arithmetic word problem solving[A]. Presented at the Meeting of the Midwestern Psychological Association， Chicago，1978.

[29]LEWIS A B， MAYER R E. Students miscomprehension of relational statements in arithmetic word problems[J]. Journal of Educational Psychology，1987，79（4）：363-371.

[30]GREENO J G. Some example of cognitive task analysis with instructional implication[C]//SNOW R E， EDERICO P F， MONTAGU W E. Aptitude， learning， and instruction hillsdale. NJ Lawrence Erlbaum Associates Inc， 1980：1-21.

[31]REED S K. Word problems： research and curriculum reform[M]. New York： Routledge， 1999：15-20.

[32]RILEY M S， GREENO J G. Developmental analysis of understanding language about quantities and of solving problems[J]. Cognition and Instruction，1988（5）：49-101.

[33][64]CUMMINS D D， KINTSCH W， REUSSER K， et al. The role of understanding in solving word problems[J]. Cognitive Psychology，1988，20（4）：405-438.

[36]付建慧，韋小滿.小學分數問題解決的認知模型研究[J].考試研究，2016（1）：82-89.

[38]楊海清，龐象辰，周碧光，等.幼兒數概念和運算能力的發展[J].心理科學雜志，1985（5）：57-59.

[39]仇佩英.幼兒數概念形成及加減運算掌握情況調查[J]. 上海教育科研，1986（4）：25-26.

[40]周晶.5～7歲兒童數學過程性能力構成要素探索與模型建構[J].學前教育研究，2018，278（2）：12-24.

[41]NUNES T， BRYANT P， EVANS D， et al. Assessing quantitative reasoning in young children [J]. Mathematical Thinking and Learning，2015，17（2-3）：178-196.

[42]LEIGHTON J P， GIERL M J， HUNKA S M. The attribute hierarchy method for cognitive assessment： a variation on tatsuokas rule-space approach[J]. Journal of Educational Measurement，2004，41（3）：205-237.

[43][57]GIERL M J， WANG C， ZHOU J. Using the attribute hierarchy method to make diagnostic inferences about examinees cognitive skills in algebra on the SAT[J]. Journal of Technology， Learning， and Assessment，2008，6（6）：1-53.

[44]丁樹良，楊淑群，汪文義.可達矩陣在認知診斷測驗編制中的重要作用[J].江西師范大學學報（自然科學版），2010（5）：490-494.

[45]丁樹良，汪文義，羅芬.認知診斷中Q矩陣和Q矩陣理論[J].江西師范大學學報（自然科學版）2012，36（5）：441-445.

[47]JUNKER B W， SIJTSMA K. Cognitive assessment models with few assumptions， and connections with nonparametric item response theory[J]. Applied Psychological Measurement，2001，25：258-272.

[48]HARTZ S M. A bayesian framework for the unified model for assessing cognitive abilities： blending theory with practicality（unpublished doctoral dissertation）[D]. IL： University of Illinois at Urbana-Champaign， Champaign， 2002.

[49]TEMPLIN J L， HENSON R A. Measurement of psychological disorders using cognitive diagnosis models[J]. Psychological Methods，2006，11：287-305.

[50]MARIS E. Estimating multiple classification latent class models[J]. Psychometrika，1999，64（2）：187-212.

[51]DA LA TORRE J. The generalized DINA model framework[J]. Psychometrika，2011，76（2）：179-199.

[52]DA LA TORRE J. An empirically based method of Q-matrix validation for the DINA model： development and applications[J]. Journal of educational measurement，2008，45（4）：343-362.

[53]ORLANDO M， THISSEN D. Likelihood-based item-fit indices for dichotomous item response theory models[J]. Applied Psychological Measurement，2000，24：50-64.

[54]ORLANDO M， THISSEN D. Further investigation of the performance of S-X2： an item fit index for use with dichotomous item response theory models[J]. Applied Psychological Measurement，2003，27：289-298.

[55]TEMPLIN J， BRADSHAW L. Measuring the feliability of diagnostic classification model examinee estimates[J]. Journal of Classification，2013，30（2）：251-275.

[56]ROBITZSCH A， KIEFER T， GEORGE C A， et al. CDM： cognitive diagnosis modeling（R package version 4.6-0，2015）[R/OL].（2016-03-12）[2018-12-12]. http：//CRAN.R-project.org/package=CDM.

[58]CHEN J， TORRE J， ZHANG Z. Relative and absolute fit evaluation in cognitive diagnosis modeling[J]. Journal of Educational Measurement. 2013，50（2）：123-140.

[59]陳興國.數學課堂中問題解決教學的理論與實踐研究[D].昆明：云南師范大學，2006：8-10.

[60]MEVARECH Z， KRAMARSHI B. Critical math for innovative societies and the role of mate-cognitive pedagogies[M]. Paris： OECD Publishing，2014：2-15.

[61]CARPENTER T P， ANSELL E， FRANKE M L， et al. Models of problem solving[J]. Journal for Research in Mathematics Education. 1993，24（5）：428-441.

[62][63]KAMII C. Young children reinvent arithmetic（2nd ed.）[M]. New York and London： Teachers College Press， 2000.

[65]CARPENTER T P， HIEBERT J， Moser J. The effect of problem stricture on first graders initial solution processes for simple addition and subtraction problems[A]. The annual meeting of The American Educational Research Association. Sanfrancisco， California，1979：1-45.

[66]HEGARTY M， MAYER R E， Monk C A. Comprehension of arithmetic word problems： a comparison of successful and unsuccessful problem solvers[J]. Journal of Education Psychology，1995，87（1）：18-32.

[67]陳英和，仲寧寧，田國勝，等.小學2～4年級兒童數學應用題表征策略差異的研究[J].心理發展與教育，2004（4）：19-24.

[68]韓瑽瑽，曹仕瑩，陳英和.4～6歲兒童加減法反演律概念的發展與影響因素[J].心理發展與教育，2012（2）：121-13.

[69]任培曉.4～6歲幼兒對數學加減逆反原則理解和運用的發展研究[D].上海：華東師范大學， 2008：21.