凸顯“轉化”思想 促進智慧生長

湯利萍

（江蘇省南通市海門市三廠小學，江蘇南通 226121）

引 言

學習數學離不開解題，解題的方式可以從一定程度上暴露學習水平。但為什么很多學生做了那么多的題目，還是無法提高解題能力呢？這是一個值得數學教師深思的問題。著名數學家波利亞曾經從宏觀到微觀，對解題過程、解題思維進行了系統而又全面的論述。他認為相較于具體的解題思路、策略，解題中的數學思想更加重要。數學思想是學生解題的靈魂，它猶如一雙“看不見的手”，始終牽引著學生。因此，研究解題思想無論對于教師的教，還是對于學生的學，都具有無可比擬的效用。作為一名小學數學教師，應通過研究解題思路、策略，幫助學生掌握解題方法后面蘊含的數學思想，點亮課堂的智慧之燈。

一、數形轉化，化“抽象“為“直觀”

著名數學教育家華羅庚說過，“數形結合百般好，割裂分家萬事休”。數（數與代數）與形（圖形與幾何），是小學數學兩大最為重要的板塊。在解題中，教師要引導學生聯系數與形，以數析形、以解釋數，從而讓數與形完美結合[1]。

例如，在教學《解決問題的策略》（蘇教版五下）時，教材中有這樣一道習題：觀察每幅圖中圓的排列規律，并填空。1=1×1 1+3=4=2×2 1+3+5=9=3×( ) 1+3+5+7=16=( )×( )并且在每個算式前配上了圖形（圖形略）。在一個班進行教學時，筆者按照教材的編寫，按部就班地展開教學。結果發現，學生對教材意圖并不“領情”，他們不理解轉化思想，體會不到轉化的作用，對轉化的思想沒有形成認同，認為不轉化反而簡便一些。為此，筆者在另一個班教學時，將題目進行了巧妙的“變臉”。

直接出示“1+3+5+……+99”，開始大部分學生不知所措，幾個思維活躍的學生開始借助等差數列進行求和，但也是不得要領。顯然，學生沒有意識到這道題可運用數形轉化的思想。當學生處于“心求通而未得”的憤悱狀態時，筆者畫出了教材中的示意圖（如圖1、圖2、圖3）啟發學生。

圖1

圖2

圖3

當筆者畫到第三幅圖（圖3）時，學生恍然大悟，紛紛拿起自己的筆開始構圖。他們不僅“以小見大”，發現了算式中隱藏著的規律，探尋到解決問題的策略，而且更為重要的是，其通過數形結合探究，領略到了數學的神奇，感受到數學具有的一種內在和諧之美。

“數是形的抽象概括，形是數的直觀表現。”“數與形”之間的轉化，是小學高學段數學普遍運用的一種轉化方法，是轉化思想在數學中最生動的表現。通過“數形轉化”，不僅能讓學生認識到“數的意義”，更能讓學生理解“形的精微”。

二、動靜轉化，化“復雜”為“簡單”

數學問題，概括而言即為兩類問題：一類是靜態的數學問題；另一類是動態的數學問題。在數學教學中，動靜是相互轉化的。動靜轉化，能化復雜為簡單、化未知為已知。只有將問題轉化成我們所熟悉、已知的條件，問題才能迎刃而解。有時，靜態的問題要進行適當的動態化才能解決；有時，動態的問題需要適當的靜態化方能攻克。只有在動與靜之間實行轉化，才能凸顯問題的本質，從而辯證、靈動地解決問題[2]。

比如，在教學《平面圖形的面積》（蘇教版五上）時，遇到了這樣一道習題：求圖4中“甲三角形的面積”比“乙三角形的面積”大多少平方厘米?

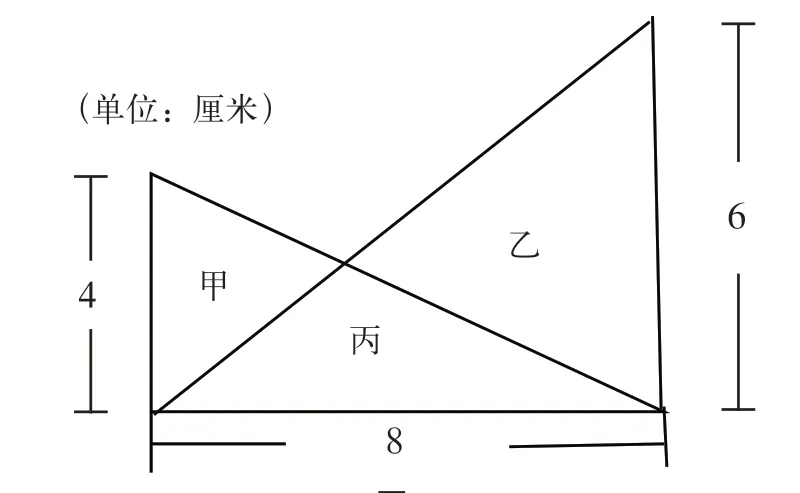
圖4

許多學生初看到問題時，往往會做靜態地分析，即學生會想方設法地直接求出甲、乙三角形的面積，然后求出面積差，這是一種常態的分析。這種分析會將問題帶入越來越復雜的境地，從而走入“死胡同”。教學中，筆者是這樣啟發學生進行轉化的：甲、乙、丙三個三角形是怎樣的三角形？（一般三角形）我們所要解決的問題是哪兩個三角形的面積差？（甲、乙兩個三角形的面積差）丙這個三角形和甲、乙兩個三角形有著怎樣的關系？通過這樣的點撥，觸發了學生的數學直覺，讓靜態的問題動態化。學生發現，甲、丙兩個三角形組成了一個直角三角形，乙、丙兩個三角形也組成了一個直角三角形，而這兩個直角三角形都可以通過已知條件求出面積。據此，學生豁然開朗：要求甲、乙兩個三角形的面積差，也就是要求甲、丙兩個三角形與乙、丙兩個三角形的面積差。將靜態的問題轉化成動態的問題，問題很快得到解決。

動靜轉化能化繁為簡、化難為易、化零為整。在數學教學中，它是一把解決數學問題的鑰匙，常常能讓學生以具化的數學問題顯出它的本質，露出它的“廬山真面目”。在數學教學中，教師就要善于運用動靜轉化思想，打破學生的思維桎梏、思維習慣，從而提高學生思維的靈通性。

三、顯隱轉化，化“陌生”為“熟悉”

在數學教學中，許多學生對題目的思考往往浮于文字表面，不能洞察題目深層的數學本質，結果導致解題時捉襟見肘，甚至舉步維艱。作為教師，要善于引導學生深入地解讀題目，并積極地展開聯想。只有這樣，才能將題目中隱含的數學本質發掘出來。如果學生對題目的解讀浮光掠影、蜻蜓點水，那么他們對題目的理解就有可能一知半解、一團霧水，從而影響題目的正確解答。作為一種具有普遍意義的思想方法，轉化在數學學習中具有十分重要的地位。

比如，在教學《梯形的面積》（蘇教版五上）時，學生遇到了這樣一道習題：一堆鋼管，最上面一層有5根，最下面一層有15根，一共11層。這堆鋼管一共有多少根？學生乍一看，紛紛列式：5+6+7+……+15。部分學生直接動筆計算，部分學習過奧數的學生開始用等差數列求和。在學生運用各種方法計算后，筆者啟發學生：這堆鋼管堆放成的是什么形狀？一語驚醒夢中人，大部分學生恍然大悟。如果將最上面一層的鋼管看成是梯形的上底，最下面一層的鋼管看成是梯形的下底，層數看成是梯形的高，那么求這堆鋼管一共有多少根不就是求梯形的面積嗎？于是，看似具有代數性質的問題，被轉化成了圖形的面積計算問題，而這正是問題的數學本質。數量關系與空間形式是小學數學的兩翼，這兩翼在數學中的邊界有時是互通的。換言之，數學中的數與形，不是涇渭分明的，而是你中有我，我中有你的交融關系。作為教師，要善于引導學生將隱性的數學本質顯性化，從而幫助學生解決問題。

結 語

授人以魚，不如授人以漁。數形轉化、動靜轉化、顯隱轉化是基本的數學方法，當前高年級的數學教學開始著重于拓展、實踐和應用，這為拓展學生思維、培養轉化思想提供了巨大的實踐空間。一切數學問題的解決過程都可以看作是一種轉化。只是有時候可以“單刀直入”，有時候卻需要“另辟蹊徑”。只有經過了“山重水復疑無路”的思維困厄，學生才能領略到問題得以解決時“柳暗花明又一村”的豁然開朗。