自覺課堂中的三角板擺放

胡玨

【摘要】七年級部分學生在學習幾何內容沒多久就開始出現明顯學習掉隊現象，造成他們困惑的原因之一就是識圖困難.教師在教學過程中充分利用三角板，讓學生在自己動手擺放的過程中，識別三角形中的角與角的關系、尋找基本圖形，由此培養學生從復雜圖形中抽象出基本圖形的意識以及學生的識圖能力.

【關鍵詞】自覺課堂;三角板;運動角度;基本圖形

一、學習困惑

七年級學生在學習幾何時常會感到困難，造成困難的原因主要有這樣的兩個方面.首先是學生自身的思維發展局限性.這個年齡階段的學生處在具體形象思維向抽象邏輯過渡的時期，且具體形象思維占據主體較多.在面對幾何學習時，他們可以熟背教師給出的定義、性質等，但將文字語言轉化成圖像信息，或者從圖像中提取信息轉化成文字語言對他們而言是有難度的.所以，我們常會見到在圖形中找不到相等的角或相等的線段的同學.

這樣，學生學習幾何渡過了最初的簡單識圖、基礎概念學習的新鮮期后，就會有一部分開始掉隊，出現在較復雜的圖形中無法尋找到基本圖形的情況，長此以往，他們就成為班里所謂的學習幾何的學困生.教師采取怎樣的教法能盡可能地幫助學生解決困惑？如何在學習幾何之初，就幫助學生培養識圖能力？

二、解決方案

經過上述分析，不難看出識圖是幾何學習的必備能力，在初中階段，大部分的幾何圖形依托三角形展開變化.如軸對稱圖形中的等腰三角形是由直角三角形沿某一條直角邊翻折得到，再如，中心對稱圖形中的平行四邊形是由三角形以某邊中點為旋轉中心，旋轉360°得到.

另一方面，三角形是指三條線段收尾順次相連圍成的封閉圖形，所以，三角形中涉及了線段和角的知識.兩塊三角板通過平移、旋轉、翻折等運動變化，又可以構造出各種圖形，三角形的全等、相似知識點的考查大多是在這些圖形中探究.

所以，以三角板為學習工具，在通過對三角板各種不同擺放的圖形過程中尋找基本圖形，以增強學生識圖能力.

同時，自覺課堂是學生活動的載體，在課堂中學生擺脫以往教師講或者在教師的引導下看紙上所畫圖形，然后根據圖形解決問題的模式，而是利用三角板這個載體讓學生在多維互動中實現“自覺地”自主生成，給學生“創造”和“再創造”的機會.由此給了學生自己搭建抽象思維與具體形象思維之間的階梯.

三、方案的具體操作

（一）三角板之初體驗——擺放靜態的圖形

教師所有教學活動展開的依據主要是立足書本，新課程提倡“材料式”的教材觀，即教材是教師教和學生學的材料，是教學資源之一，其根本特征是“范例性”.

如蘇科版七上第154頁“想一想”中要求學生“如何畫一個角等于已知角”，特別強調

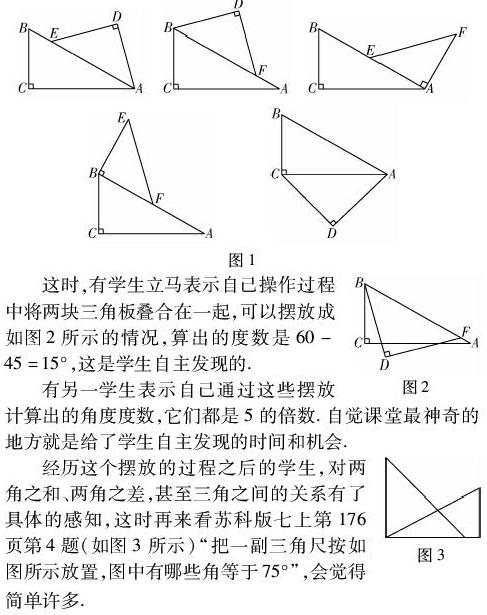
一些特殊角可以用一副三角尺畫出.三角板自身的特殊角度有30°，45°，60°，90°.除這些角度外，還可以畫出哪些角度呢？兩塊三角板不疊合在一起，可以擺放成如圖1所示.

這時，有學生立馬表示自己操作過程中將兩塊三角板疊合在一起，可以擺放成如圖2所示的情況，算出的度數是60-45=15°，這是學生自主發現的.

有另一學生表示自己通過這些擺放計算出的角度度數，它們都是5的倍數.自覺課堂最神奇的地方就是給了學生自主發現的時間和機會.

經歷這個擺放的過程之后的學生，對兩角之和、兩角之差，甚至三角之間的關系有了具體的感知，這時再來看蘇科版七上第176頁第4題（如圖3所示）“把一副三角尺按如圖所示放置，圖中有哪些角等于75°”，會覺得簡單許多.

紙上畫的幾何圖形，對學生而言，就是圖形，是抽象的.但是，三角板是學生可以拿在手中的，是具體形象的.它的出現是幫助學生實現了具體形象的物體到抽象圖形的過渡.另外，擺放三角板的過程本身就是一個要求學生參與的動手實踐過程.學生在操縱的過程中的感知體驗明顯強于單純地對著圖形看.

（二）三角板之再體驗——呈現動態過程

在學習蘇教版八上的“1.2全等三角形”這一內容時，圖形的復雜程度明顯增加，部分學生感到從圖形中找出對應的線段或角都是較難的一件事.造成這樣錯誤的原因主要還是學生自身對兩個三角形這樣的基礎圖形認識不足.在他們的意識里，線段就是一條條獨立存在的，角也是如此，并沒有從整體角度去看圖，所以，才會出現找不清楚全等三角形的對應線段和對應角的情況.

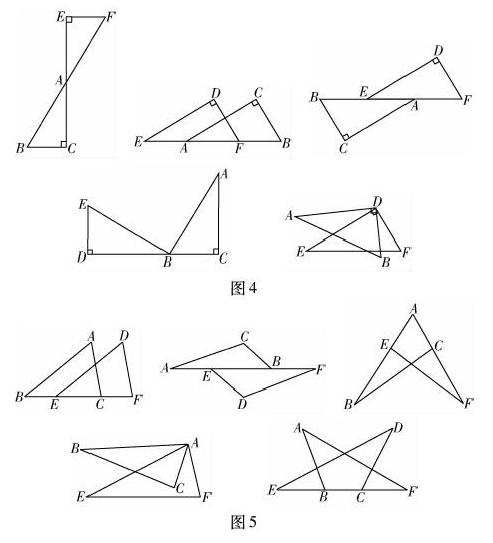
準備兩塊含30°角的三角板，運用平移、旋轉、翻折的運動方式擺放出新的圖形（兩塊三角板可以有重疊）.這樣，可以擺放出如圖4所示的典型圖形，也可以更多別的圖形.

在學生擺放時，要求把擺放出的圖形畫下，并找出圖中相等的線段和相等角.這樣，三角板再次幫助學生實現了從具體實物到抽象圖形的過渡.特別是因為經歷了自己動手擺的過程，對全等三角形的對應線段、對應角感受深刻，有效突破了在學習這一知識時的識圖難點.

在從運動的角度擺放兩塊全等的直角三角板后，教師再將其一般化為兩個全等的銳角三角形或鈍角三角形時（如圖5所示），學生自然會聯想到之前擺放直角三角板時所找的相等線段、相等角.這時，再要求學生分別說出圖5中的一個三角形經過怎樣的運動就與另一個三角形重合.

從運動的角度看圖形讓學生在識圖時有了整體意識，不再是孤立地看線段和角，而是站在了線段或角是屬于哪個圖形這樣更高的位置，為解決判斷兩個三角形是否全等的問題作了充足的知識儲備.另外，也為以后要學習的判斷兩個三角形是否相似做了鋪墊.

經歷了這些動態三角板擺放出的各種圖形后，相信很多善于觀察的學生發現圖形可以是千萬種，但是，這些諸多的不同中總有些相同之處.這些相同之處，就是他們自己抽象出的基本圖形.這種抽象如果單純地依靠學生自己的空間想象力實現是有一定難度，但是有了三角板這個實物擺放，明顯是幫助他們降低了思維難度.

幾何圖形之間的聯系既表現在它們的共同性，也表現在它們的差異性上.所以，教師在教學時要注意舍得花時間給學生，讓他們觀察復雜圖形，從找出與他們題目間的共性與差異性.培養他們從復雜圖形中抽象出本質的意識和能力.同時，使同學們在對比與查找的過程中，享受到數學學習的快樂，培養起學生學習數學的興趣.

綜上所述，三角板是幫助學生破解識圖難的極好的工具.它是學生從具體形象思維向抽象邏輯思維過渡的橋梁.蘇科版教材中也一再用到了三角板作為幾何學習的切入口.在教學時，教師可以充分發揮三角板的妙用，給足學生擺放的時間，讓他們在具體感知中熟悉線段、角，摸索歸納出基本圖形，為以后的學習打下堅實的基礎.

【參考文獻】

[1]王鋒.玩轉三角板 猜想自然來[J].初中生輔導，2018（Z1）：95-98.

[2]汪健.巧用三角板，優化初中數學課堂[J].考試與評價，2014（3）：57.

[3]何笑琴.優化課堂教學 提高學生素質[J].黑河教育，2001（2）：22-23.