基于數學抽象的培養與提升

☉江蘇省張家港市沙洲中學 施利文

一、問題的提出

在《普通高中數學課程標準（2017年版）》一文中，對于“課程基本理念”這一部分第一次創新性地提出：“高中數學課程以學生發展為本，落實立德樹人根本任務，培育科學精神和創新意識，提升數學學科核心素養”.高中階段，結合數學學科的特點，歸納總結出了六大核心素養：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析.

其中，對于數學抽象這一重要的核心素養，其是指舍去事物的一切物理屬性，進而得到數學研究對象的素養.數學抽象是數學學科的基本思想，也是一種特殊素養，是貫穿于整個數學教學與學習的一條隱形思維鏈條.那么如何在數學教學、數學學習及數學解題的過程中進行有效、合理、科學地培養與提升學生的數學抽象呢？

二、問題的解決

1.從概念入手進行數學抽象

數學概念是對具體的數學問題進行抽象與概括，從實際問題中區分、抽象、歸納、總結出研究對象的本質特征，通過合理抽象、科學概括、合理歸納，從而得以認識和理解所研究的數學對象與數學問題，最后再結合相關的數學知識與數學方法來進行分析與處理.

例1（2019屆江蘇省常州市武進區高三第一學期期中考試·14）若正實數x，y滿足x2-xy+y2=9，且|x2-y2|＜9，則xy的取值范圍為______.

分析：根據條件引入參數，利用雙變量換元法進行處理，把取值范圍問題轉化為對應的不等式問題，通過求解相應的二次不等式來求解對應的代數式的取值范圍，即可確定xy的取值范圍.

解：設x-y=m，xy=n＞0.

由x2-xy+y2=9，整理有（x-y）2+xy=9，可得m2+n=9，從而n=9-m2≤9.

又|x2-y2|2=（x+y）2（x-y）2=［（x-y）2+4xy］（x-y）2=（m2+4n）m2＜81，

所以將m2=9-n代入，整理有（9+3n）（9-n）＜81，解得n＜0（舍去）或n＞6.

綜上所述，n∈（6，9］，即xy∈（6，9］.

故填答案：（6，9］.

點評：涉及代數式相關值的求解或取值范圍問題，經常通過引入參數來處理與轉化.結合題目條件，通過數學抽象，借助參數的引入并賦值，再利用參數的運算，通過待定系數法的應用，借助二次不等式的求解來達到確定相應的代數式的取值范圍的目的.在函數與方程的有效轉化與綜合的過程中，巧妙地滲透著數學抽象思維及其應用.

2.從公式入手進行數學抽象

數學公式是從數學過程中抽象并歸納出來的，利用數量關系、參數關系、邏輯關系及其他相應關系總結與歸納出來的.因此利用數學公式中所包含的數學抽象來破解相應的數學問題，也是數學抽象的反饋與應用.

例2（2018·全國Ⅱ理·15）已知sinα+cosβ=1，cosα+sinβ=0，則sin（α+β）=______.

分析：借助條件給出兩個相應的三角函數的關系式，利用三角函數公式，通過具體的特殊角加以特殊化處理，先入為主，進而在特殊角的情況下確定相應的三角函數值的取值.

解：根據填空題的特征，其答案具有一般性——定值，那么可以借助三角函數公式，取特殊角來處理：α=150°，β=60°.

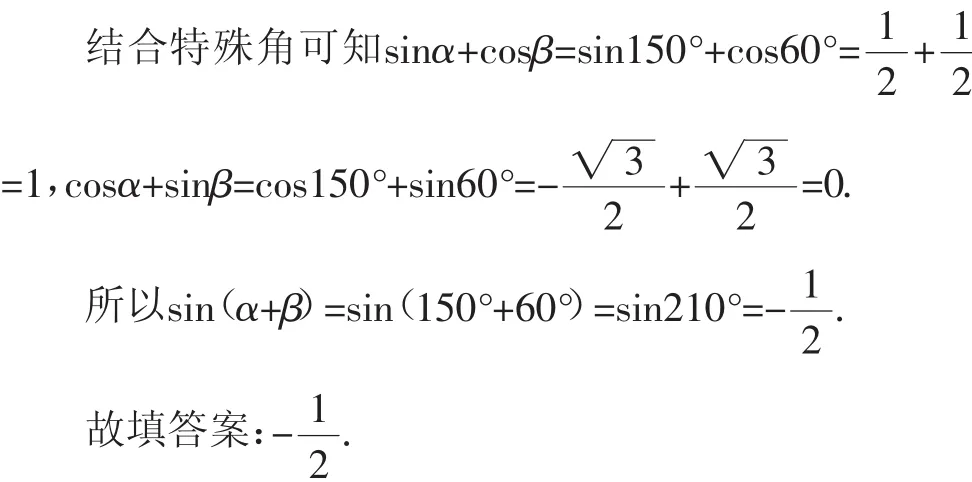
點評：借助三角函數公式，以特殊代表一般，進而達到求解的目的.在處理一些選擇題或填空題時，經常借助數學公式加以數學抽象，先入為主，巧妙地構造滿足公式的特殊值來進行轉化與處理，達到以特殊代表一般的目的.從而巧妙地省去中間的三角恒等變換，簡化運算，提升效益.

3.從圖形入手進行數學抽象

從數學圖形中反映并抽象出數學概念、數學數量、數學參數等之間的關系，以及變化規律、基本性質等.借助數學圖形，可以從中抽象出一般性的規律與結構，進而為破解數學問題指明方向與提供條件.

例3孔明鎖，也叫魯班鎖，是廣泛流傳于中國民間的智力玩具，起源于古代漢族建筑中首創的榫卯結構.圖1是六柱孔明鎖，由6根相同的開槽（即榫卯結構）的正四棱柱組合而成.圖2中的邊長為1的正方形網絡中粗線畫出的是該六柱孔明鎖的正視圖，則該六柱孔明鎖的表面積為______.

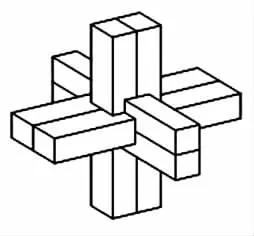
圖1

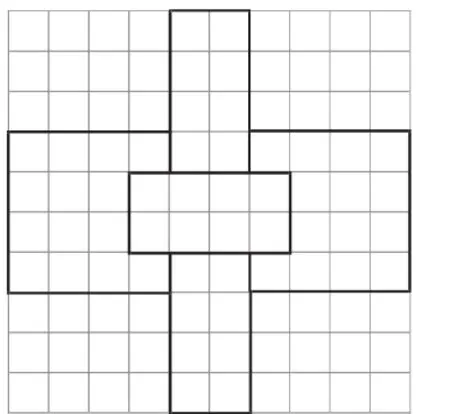
圖2

分析：借助數學文化的闡述，對于復雜圖形的表面積問題，可以借助于三視圖中的投影圖形加以數學抽象并進行歸納總結，利用投影面積的計算來達到目的.

解：由六柱孔明鎖的正視圖可知，投影面積為10×4+2×3×2=52.

而六柱孔明鎖的所有表面共由6個投影面組成，所以該六柱孔明鎖的表面積為52×6=312.

故填答案：312.

點評：借助對數學圖形的分析、歸納并加以抽象，明確給出六柱孔明鎖的所有表面是由6個投影面所組成的，且每一個投影面都與正視圖中的投影面相吻合，因此通過數學抽象總結歸納出規律進行破解.

4.從方法入手進行數學抽象

數學方法是借助于數學知識來歸納并總結出具有可操作性、可拓展性的破解問題的基本思維方式，是數學抽象的具體體現方式之一，也是數學抽象的具體體現、高度概括、方法類比、準確表達及思維應用等系統性的體現.可以通過數學抽象出來的數學方法來有效地解決問題，提升能力.

例4 （2019屆江蘇省鹽城市高三期中考試·12）已知函數f（x）=（x+m）-（m+1）x在R上單調遞增，則實數m的取值集合為______.

分析：涉及函數的單調性問題，往往從導數方法入手，利用導數的求解，結合不等式恒成立加以數學抽象，進而達到破解參數的取值范圍的目的.

解：由題可知f′（x）=（x+1+m）ex-x-（m+1）=（x+1+m）·（ex-1）≥0在R上恒成立.

當x≤0時，ex-1≤0，則必須x+1+m≤0恒成立，解得m≤-1；

當x＞0時，ex-1＞0，則必須x+1+m≥0恒成立，解得m≥-1.

綜上可得m=-1.

故填答案：{-1}.

點評：不同的數學知識具有比較常規的數學方法，而有關函數的單調性問題，一般采用導數法來破解.借助數學抽象所歸納出來的數學方法來進行破解，是解決數學問題的首選，也是常規解題規律的首選.

三、感悟與反思

其實，數學核心素養并非是另起爐灶的“新搞法”、“新噱頭”，而是解決數學問題所必須具備的核心知識、基本技能技巧，以及與之相關的數學運算能力、邏輯推理能力、抽象與想象能力，還有遇見問題時的思維方式和解決問題時的基本模式.

數學抽象是通過對高中數學課程的教學與學習，逐步抽象出相應的數學概念、公式、命題、圖形、方法和體系等，養成思考問題的一般性習慣，并進一步歸納總結，進而把握數學問題的本質屬性，達到抽象概括、化繁為簡的目的，從而有效地借助數學抽象的核心素養與思維方式來思考、分析與解決問題.