基于自適應權重粒子群算法的脫硝系統建模

白建云 ,雷秀軍 ,斛亞旭 ,侯鵬飛 ,賈新春

(1.山西大學自動化系，山西 太原 030013；2.山西大學數學科學院，山西 太原 030006)

0 引言

近幾年，隨著我國對環境的要求越來越嚴格，對于火電廠中的SOX、NOX以及煙塵也有了更加嚴格的要求。而與其他鍋爐相比，循環流化床(circulated fluidized bed，CFB)鍋爐在燃燒過程中產生的NOX相對較少，這對脫硝工作非常有利。CFB鍋爐一般采用選擇性非催化還原(selective non-catalytic reduction，SNCR)煙氣脫硝技術，使煙氣排放達到國家標準。

在SNCR脫硝過程中，選擇一個相對精確的模型有利于有效地控制出口NOX濃度，同時可以節約尿素使用量和減少氨逃逸。鐘祎勍等[1]通過分析SNCR脫硝控制系統的動態特性，對其建立高精度的最簡控制模型。白建云等[2]利用BP神經網絡建立NOX生成質量濃度預測模型，實現了NOX生成質量濃度的軟測量，并應用于實際發電過程系統。朱竹軍等[3]設計了一種基于專家模糊的SNCR脫硝系統自動控制策略，解決了SNCR脫硝系統長期以來不能100%實現NOX自動控制的問題。秦天牧等[4]利用多尺度核偏最小二乘(multi-scale kernel partial least squares，MKPLS)方法，建立了選擇性催化還原(selective catalytic reduction，SCR)系統模型。方賢等[5]通過采用粒子群算法，對TWSVM的核參數和懲罰因子經行尋優，并建立SCR脫硝效率預測PSO-TWSVM。以上都是對生成的NOX進行預測和軟測量，或者對SCR脫硝系統進行最簡建模，然而對于SNCR脫硝系統建模的研究卻很少。

系統建模方法兩種方法，分別為機理建模和試驗建模。其中：試驗建模可以在不清楚系統內部結構的前提下，根據系統的輸入輸出數據來建立系統的模型[6]。循環流化床SNCR脫硝系統是一個大慣性、大遲延、非線性的對象，其內部結構通常無法獲得。因此，本文利用粒子群算法對SNCR脫硝系統進行試驗建模。該方法可同時辨識出SNCR脫硝系統的遲延。采用實際運行數據進行模型驗證，結果證明了所建模型的有效性。

1 SNCR脫硝系統的模型選擇

1.1 SNCR脫硝系統簡介

循環流化床SNCR脫硝工藝流程如圖1所示。

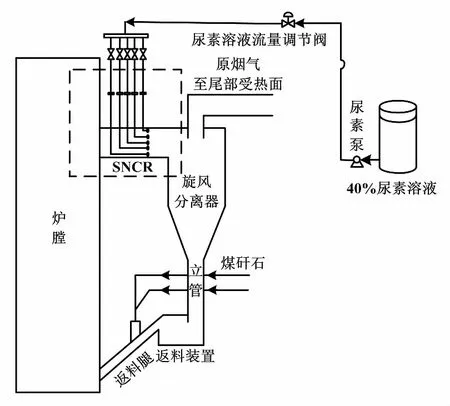
圖1 循環流化床SNCR脫硝工藝流程圖

某電廠采用尿素作為還原劑，利用尿素泵將儲存罐中的40%尿素溶液輸送到系統管道中，再經過流量調節閥控制噴入旋風分離器前煙道內的尿素流量，進而控制生成NOX的濃度。其中安裝的噴槍共21只。

循環流化床鍋爐SNCR脫硝系統的反應器為旋風分離器。旋風分離器溫度為800～1 100 ℃，恰好是發生化學反應的在最佳溫度，因此不需要催化劑。還原劑經過噴槍和管道后進入分離器前部煙道與NOX進行反應，在反應器內熱解成為NH3與煙氣中的NOX進行脫硝反應生成N2。某電廠運用尿素溶液作為還原劑，在酸性條件下與NOX發生還原反應，最終產物為N2、CO2、和H20，不會造成二次污染。以尿素為還原劑來脫除NOX的主要化學反應如下：

6NO2+4CO(NH2)2→7N2↑+4CO2↑+8H2O

6NO+2CO(NH2)2→5N2↑+2CO2↑+4H2O

NO+NO2→N2O3

N2O3+H2O→2HNO2

2HNO2+CO(NH2)2→2N2↑+CO2↑+3H2O

1.2 模型的選擇

目前，循環流化床SNCR脫硝控制系統中，主要通過控制尿素溶液或氨水流量閥門來控制噴入催化劑的量，進而在分離器內進行脫硝。這一過程可以分為兩類模型，第一類是尿素流量閥門開度到尿素流量的模型，第二類是尿素流量到煙囪出口NOX濃度的模型。本文主要采用帶有自適應權重的粒子群建模方法建立第二類模型[6-7]。

循環流化床機組SNCR脫硝系統NOX排放濃度受總煤量、尿素流量、總風量、旋風分離器入口的溫度、機組負荷、稀釋水的流量等一系列因素的影響。當機組處于穩定負荷工況運行時，總煤量、總風量以及旋風分離器入口溫度基本保持不變，且保持尿素溶液濃度為40%。因此，煙囪出口排放的NOX濃度主要由尿素溶液流量決定。

在數據采集之前，要選擇采樣周期。采樣周期的選擇取決于被辨識對象的主要頻帶中的最高頻率，但是在辨識前估計最高頻率是非常困難的。采用前人經驗獲得采樣周期為12 s。通過從現場分散控制系統(distributed control system,DCS)系統每隔12 s采集一次數據，現場采集的數據由于各種原因不可避免地帶有誤差，所以需要剔除異常值，進行濾波處理后選取有效的具有代表性的數據[10,12]。

傳遞函數模型的表達，是任何一個系統處于某個平衡點時，輸出的增量與輸入的增量之間的函數表達，即系統在平衡狀態時，系統的輸入輸出以及它們的各階導數也為零，它們的各階導數也為零。因此,需要對原始的開環數據進行零初始值處理。原始數據的輸入輸出分別為u(k)和y(k)，經過零初始值后的數據為:

(1)

式中：N為零初始值點數據個數。

經過采集數據以及數據的預處理后，建立以40%尿素溶液流量為輸入，從而生成NOX濃度為輸出的模型。以試驗機組為例，選擇140 MW、170 MW、200 MW三個典型工況，進行尿素溶液流量與NOX排放濃度之間的模型辨識。

在實際應用過程中，通常用一階慣性時滯系統或者二階慣性時滯系統就可以描述被控過程特性。但是經過對循環流化床SNCR脫硝系統工藝流程進行分析，以及查閱參考張志超等人對SCR脫硝系統建立的模型后，得出循環流化床SNCR脫硝系統具有大遲延、大慣性、非線性強等特點[6]。本次尿素溶液流量到生成NOX濃度的模型采用帶有純遲延的四階慣性環節作為系統待定模型的傳遞函數，具體形式為：

(2)

式中：K為系統開環增益；T為慣性時間；τ為純遲延時間；n為系統階數

本文通過自適應權重粒子群算法對傳遞函數的四個參數進行辨識，從而得到SNCR脫硝系統模型。

2 基于自適應權重PSO算法的模型辨識

粒子群優化(particle swarm optimization，PSO)算法，是一種模擬鳥類在覓食過程中通過信息共享實現最優化覓食的仿生尋優算法[8]。

粒子群算法的數學過程描述如下。假設在一個D維查詢空間中，n個粒子所對應種群為X=(X1,X2,…,Xn)，其中，第i粒子的位置為Xi=(xi1,xi2,…,xiD)T(是問題所要找的隱含解)，將其代入目標函數，就可得到每個粒子在該位置的適應度值。設個體極值為Pi=(Pi1,Pi2,…,PiD)T，群體極值為Pg=(Pg1,Pg2,…,PgD)T，第i粒子運動速度Vi=(Vi1,Vi2,…,ViD)T。在第k次循環計算過程中，利用目前群體極值和個體極值確定下一次的更新粒子速度和位置，更新所對應的公式為：

(3)

(4)

式中：ω為慣性權重；c1、c2為加速度因子；r1、r2為分布于[0，1]的隨機數，通過對粒子的速度和位置進行限制，防止盲目搜索[9]。

上述算法是普通粒子群算法。由于普通的粒子群算法在全局搜索能力上相對較弱，只可以找到局部最優解，對于實際的需求還遠遠不夠。因此，需要對慣性權重進行更新。根據當前粒子的適應度值與平均適應度值對慣性權重進行更新[10]。慣性權重更新公式如下。

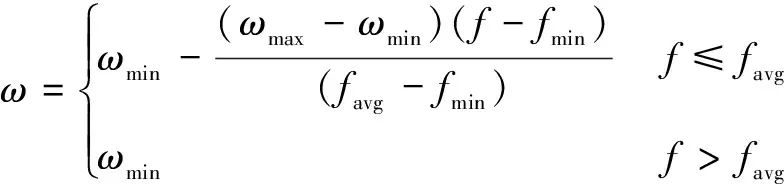
(5)

式中：ωmin、ωmax分別為慣性權重ω的最大值、最小值；f為粒子此時適應度函數值；favg與fmin分別為當前所有粒子的平均適應度函數值和最小適應度函數值。

帶有自適應權重粒子群算法參數辨識方法步驟如下。

①初始參數設置。它包括變量個數、種群規模、待辨識參數范圍、慣性因子變化范圍、粒子速度范圍、迭代次數、加速度因子等。②種群初始化。通過隨機產生的種群來計算每一個時刻的性能指標值，進而得到個體最佳值與全局最佳值。③種群更新。按照參數設定和權重更新公式計算慣性因子值、種群個體移動速度，更新種群，把計算出來的性能指標與個體和種群的歷史最優值進行比較，并將二者的歷史最優更新。④如果滿足終止條件，則停止尋優；反之，返回步驟②繼續尋優。⑤如果達到循環次數，則停止尋優；反之，返回步驟①再次尋優。實現多次迭代尋優，從而得到全局最優值。參數辨識算法流程如圖2所示。

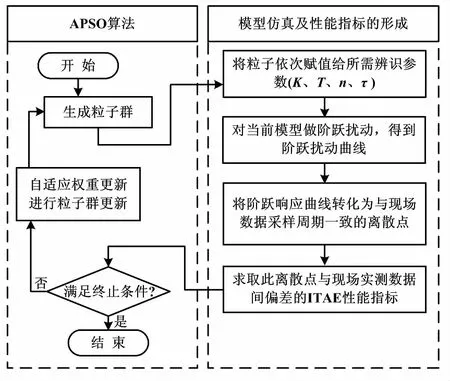
圖2 參數辨識算法流程圖

3 SNCR脫硝系統建模與驗證

利用Matlab編寫粒子群算法辨識主程序及計算辨識優化目標函數子程序，以200 MW負荷工況為例，選擇150組開環試驗數據，對對象數學模型參數進行辨識。首先，對200 MW工況下的歷史開環數據進行零初始值處理，得到尿素溶液流量數據和出口NOX濃度數據零初始值處理結果。尿素溶液流量數據處理前后對比如圖3所示。出口NOX濃度數據處理前后對比如圖4所示。

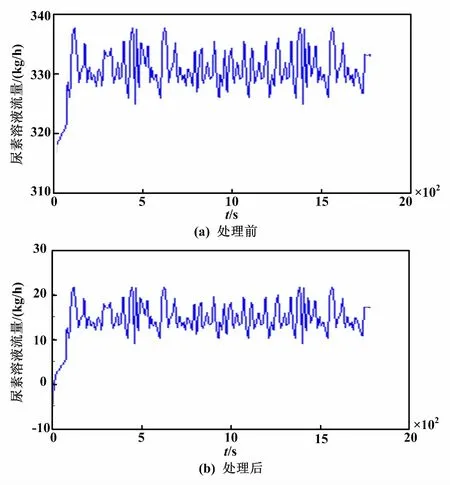
圖3 尿素溶液流量數據處理前后對比圖

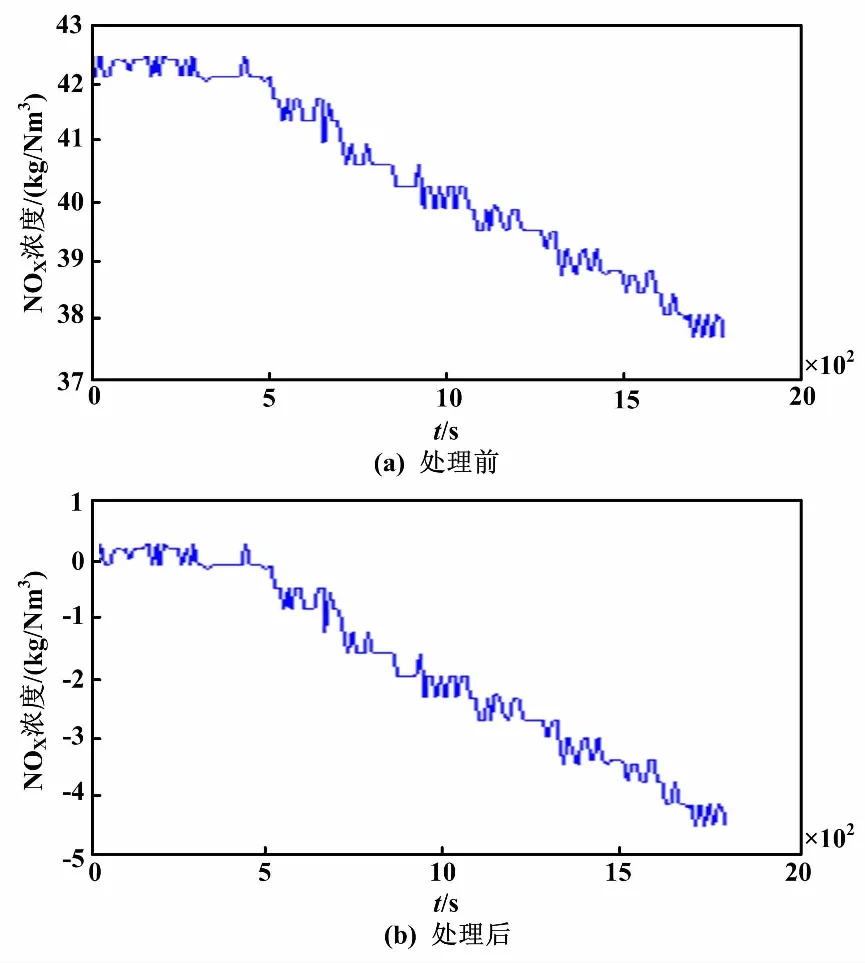
圖4 出口NOX濃度數據處理前后對比圖

從圖4可以看到，經過初始值處理后的NOX濃度數據變為負數，但是這樣不會影響模型的建立。利用帶有自適應權重的粒子群算法進行模型辨識，仿真參數設置如下。

參數尋優區間：K∈[-10，10]，T∈[20，400]，N∈[2，5]，τ∈[20,200]。

粒子個數：200。

進化代數：80。

慣性權重：ωmin=0.4,ωmax=0.9。

學習因子：[0.6 0.8]。

加速度因子：c1=2,c2=2。

速度范圍區間：V∈{[-1，1]、[-1，1]、[-1，1]、[-1，1]}。

仿真結果對應參數值為：K=-1.46;T=400;N=4;τ=-165。同理可以分別得出負荷為140 MW、170 MW時，SNCR脫硝系統從40%尿素溶液到生成NOX濃度的開環模型。

三個工況模型辨識結果如表1所示。

表1 三個工況模型辨識結果表

本文以200 MW負荷工況下辨識出的模型為例，進行驗證。選擇現場中尿素溶液流量從310 kg/h升高到330 kg/h的階躍擾動。為了驗證所建立模型的穩定性，將階躍擾動分別加到辨識模型和實際測量的數據中，觀察兩者的輸出曲線。200 MW模型辨識結果與實測數據對比如圖5所示。

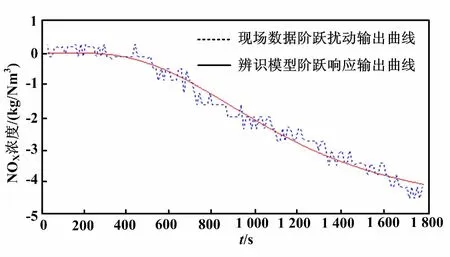
圖5 200 MW模型辨識結果與實測數據對比圖

200 MW模型輸出和實際數據之間的誤差如圖6所示。

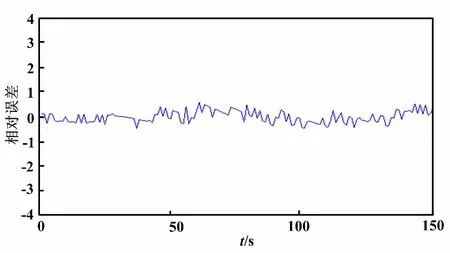
圖6 200 MW模型輸出和實際數據之間的誤差圖

140 MW模型辨識結果與實測數據對比如圖7所示。

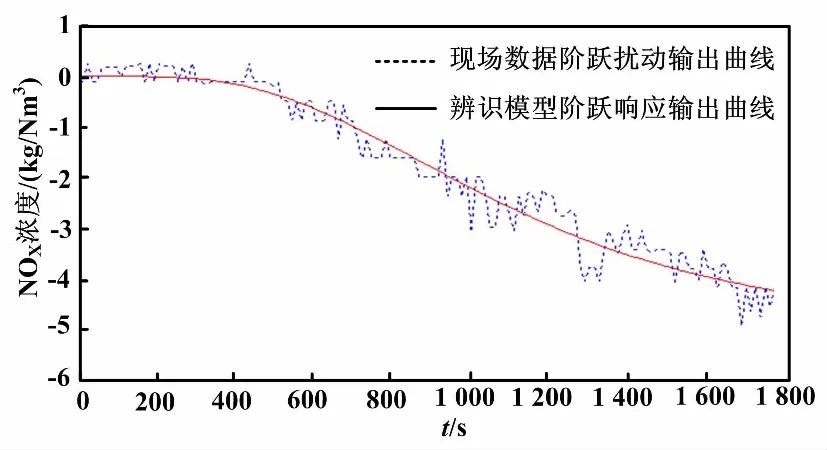
圖7 140 MW模型辨識結果與實測數據對比圖

170 MW模型辨識結果與實測數據對比如圖8所示。

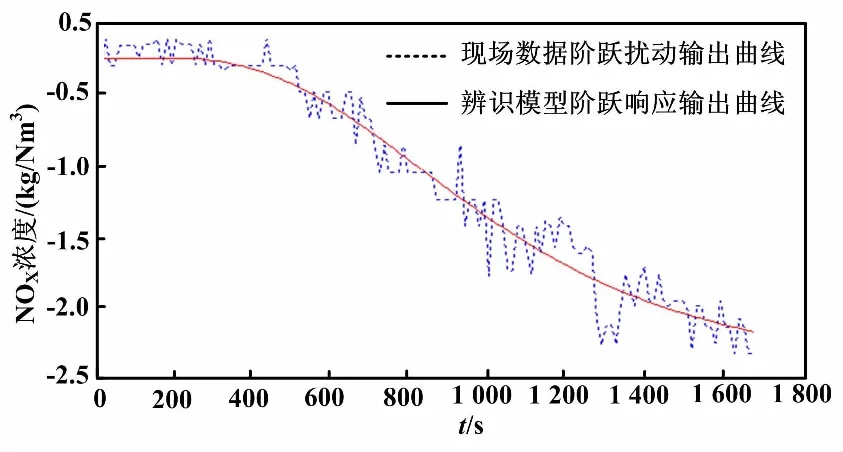
圖8 170 MW模型辨識結果與實測數據對比圖

從圖5～圖8可以看出：基于自適應權重粒子群算法辨識得到的模型在階躍擾動下的輸出曲線基本上與現場采集回來的數據在階躍擾動下的輸出曲線吻合，模型輸出與實際數據的相對誤差在±0.5左右，開環模型可以用于SNCR脫硝系統的控制。

同理，可以對其余兩種工況下的模型進行驗證，輸出曲線結果大致相同，誤差也在可接受范圍內。綜合上述三種工況辨識出來的模型，基本上與實測數據相符合。通過辨識出的模型參數，得到三個工況下的傳遞函數，為循環硫化床SNCR脫硝控制中從尿素流量到生成NOX濃度建立了可靠模型。所建模型有利于對生成的NOX濃度進行有效控制，并可以減少氨逃逸。

4 結束語

本文通過采集某電廠200 MW循環流化床機組SNCR脫硝系統的歷史開環數據，對數據進行去除異常值和零初始值處理。根據專家經驗和熱工過程，確定SNCR脫硝系統中從尿素溶液流量到出口NOX濃度的模型。采用基于自適應權重的PSO算法，辨識出三個不同工況下的模型參數，并對不同工況模型進行驗證。仿真結果表明，基于自適應權重的PSO算法在SNCR脫硝系統中的模型參數辨識具有很好的效果。辨識出的模型為先進的智能控制算法在火電廠SNCR脫硝系統應用提供了模型基礎，進而可以更好地控制NOX排放并減少氨逃逸，最終實現減少還原劑的使用量，提高經濟效益。該成果推動了智能算法在其他工業過程中的應用。