低軌衛星廣播星歷參數設計

方善傳，杜 蘭，高 燕

(1.太原衛星發射中心技術部，山西 太原 030027；2.信息工程大學 地理空間信息學院，河南 鄭州 450001)

0 引言

傳統的導航增強系統都是采用地球同步軌道(Geosynchronous Earth Orbit，GEO)衛星作為通信媒介，提供差分校正值和完好性數據[1]。雖然GEO僅需要少量的衛星就可以向全球用戶發播導航信息，但是其軌道資源有限。按照國際電信聯盟規定，GEO衛星每1.5°可部署一顆，總共只有240個軌位[2-3]；其獨特的高軌、靜地和頻繁的軌道定點機動，導致其軌道精度較差[4-5]；較高的軌道導致信號延遲較多，且用戶接收到的衛星信號較弱，容易受到干擾。

LEO衛星作為導航增強系統的新興力量，具有獨特的優勢。其軌道高度低，軌道資源較為豐富。隨著衛星發射技術的進步，LEO衛星發射成本迅速降低，遠低于發射中/高軌衛星。隨著星載GNSS測定軌技術的成熟和輔助加速度計在攝動力測定中的應用，LEO衛星定軌精度已經優于分米級[6-7]。同時，由于LEO衛星軌道高度低，離地面站較近，衛星信號更強，信號延遲更少[8]。基于LEO的導航增強系統成為目前LEO衛星應用推廣發展的趨勢之一[9]。

導航電文是衛星導航系統頂層設計的重要組成部分，其結構設計直接決定了首次定位時間、通信效率和可擴展性等關鍵性能指標。而廣播星歷是導航電文的核心，其表示方式直接決定了衛星軌道精度和通信效率等[10]。目前，廣播星歷參數主要有兩大類：一類是基于軌道根數型的廣播星歷，GPS，BDS，GALILEO，QZSS都是使用基于軌道根數型的廣播星歷[11-12]；另一類是基于軌道狀態型的廣播星歷，GLONASS正在使用這種類型的廣播星歷[13-14]。對于低軌導航增強衛星，目前還沒有成熟的廣播星歷模型可供使用。

在LEO衛星的星歷設計方面，文獻[15]參照GPS廣播星歷16參數擬合法特點，根據約1 000 km高度LEO衛星的軌道特征，設計了一套針對LEO衛星的25參數星歷模型，擬合2 h衛星位置誤差的均方差小于10 m，部分弧段擬合誤差小于25 m，但擬合時間過長，擬合精度較差，參數較多。文獻[16]將GPS 16參數星歷模型直接用于LEO衛星，星歷擬合精度與GPS衛星相當，擬合時長縮短為10～20 min，為確定LEO衛星的星歷擬合時間提供了參考。由于LEO導航增強衛星大多數采用近圓軌道，而軌道根數型星歷用于近圓軌道擬合時，開普勒根數的強負相關性和擬合算法的矩陣嚴重病態，會嚴重影響擬合算法迭代收斂的速度和擬合精度。

本文根據軌道列表型星歷模型的無奇點特性，設計了2種基于軌道狀態型的16參數星歷模型。首先，針對300～1 000 km高度的低軌衛星，根據其攝動力量級和短期動力學特性，在ECEF坐標系下構建經驗力模型，利用二次多項式/周期項+常數項來吸收經驗力攝動加速度的影響。該方法既保留了軌道列表型星歷的無奇點特性，又能夠利用較少的參數進行高精度的星歷擬合。將擬合時間設計為用戶的衛星最大可見時間，降低用戶星歷更新頻率。采用300～1 500 km高度高精度軌道預報數據，通過星歷擬合驗證了設計的2種星歷模型。擬合結果表明，方案1的URE(User Range Error)精度優于11 cm，方案2的URE精度優于9 cm。

1 LEO廣播星歷參數設計

廣播星歷的設計原則是利用盡量少的參數實驗高精度的衛星位置擬合，減少通信資源損耗，縮短用戶首次定位時間。通常廣播星歷擬合精度要求URE小于10 cm。因此廣播星歷設計時需要考慮主要攝動力，對于LEO導航增強衛星，其受到的主要攝動力為地球扁率J2攝動、大氣阻力攝動、日月引力攝動和其他非球形引力攝動主項。其中，地球扁率攝動力模型簡單，可以直接采用。對于力模型計算較為復雜的大氣阻力和日月引力攝動，通常簡化處理方式是針對其短期內的攝動加速度變化規律，采用簡單的數學函數進行模型逼近，即經驗力建模。對于短期軌道積分，更小量級的攝動力則可以忽略。

在主要攝動力影響下，存在趨勢性和周期性變化的攝動力在短弧段內具有如下規律[17]：

① 由于大氣阻力的影響，衛星位置分量呈現逐漸減小的趨勢性變化，可考慮用多項式吸收趨勢項經驗力的影響；

② 由于日月引力和其他攝動主項的影響，攝動力隨著衛星運行呈現周期性變化，變化周期與軌道周期相同，可考慮用二次多項式或三角函數吸收周期項經驗力的影響。

1.1 廣播星歷參數模型

在經驗力的趨勢性和周期性變化分析基礎上，綜合考慮參數個數、擬合精度以及用戶衛星位置速度的計算復雜度等，提出了2種星歷模型方案。

1.1.1 方案1

采用二次多項式來擬合經驗力的攝動加速度，即

(1)

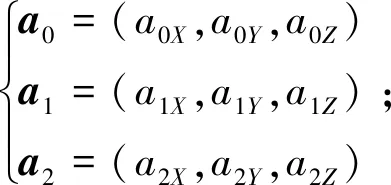
設計的16參數 LEO廣播星歷在toe時刻表示為：

x16=(toe，x，y，z，vx，vy，vz，a0X，a0Y，a0Z，a1X，a1Y，a1Z，a2X，a2Y，a2Z)T。

1.1.2 方案2

采用常數項加周期項來擬合經驗力的攝動加速度，即

(2)

設計的16參數 LEO廣播星歷在toe時刻表示為：

x16=(toe，x，y，z，vx，vy，vz，a0X，a0Y，a0Z，AX，AY，AZ，BX，BY，BZ)T。

1.2 擬合算法

廣播星歷的參數x需要通過一段時間內精密外推的衛星位置序列R(默認為真值，m×3階，含m組衛星位置序列)擬合得來，其計算方法有很多，本文使用最小二乘法進行擬合[18-20]。

設參考歷元星歷參數的狀態向量為x(t0)，其概略初值可以取為：

x(t0)=(t0，x，y，z，vx，vy，vz，0，0，0，0，0，0，0，0，0)T，

式中，(x，y，z，vx，vy，vz)為t0時刻衛星位置分量，其他攝動參數初值取為0。

衛星位置向量序列R與參考歷元星歷參數x(t0)之間的關系為：

R=Y(x(t0)，t)，

(3)

式中，t為m組衛星位置序列對應的時間向量序列；函數Y(x(t0)，t)的算法即是前面介紹的用戶算法。使用最小二乘法對式(3)進行線性化之后得到：

(4)

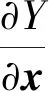
令y為衛星位置真值與計算值Y(xi(t0)，t)之差，即

y=R-Y(xi(t0)，t)，

(5)

令

(6)

Δx=x-xi，

(7)

略去式(4)中的二階及其以上的高階項，可得：

y=AΔx，

(8)

根據最小二乘法原理，可得Δx的最優估值為

Δx=(ATA)-1ATy，

(9)

迭代公式為：

xi=x(t0)+Δx，

(10)

迭代結束的條件為：

|δi-δi-1|/δi-1<ε，

(11)

式中，ε是預先給定的收斂條件，其值越小，迭代次數越多，迭代精度越高；δi為第i次迭代時y中的誤差統計值，其計算方法為

(12)

1.3 用戶算法

用戶接收到衛星播發的軌道列表型星歷后，需要通過星歷提供的廣播星歷參數，計算出衛星在可見時間內某一時刻的位置速度[22-23]。

(13)

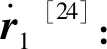
(14)

1.4 LEO的星歷擬合精度指標

URE性能指標反映了導航星歷和預報鐘差的精度，是計算星歷和鐘差誤差對定位影響的一個重要評價指標[25]。在衛星導航系統中，廣播星歷參數擬合的限制性要求是擬合結果等效URE損失小于0.1 m[26]。URE的來源主要是軌道外推誤差和鐘差誤差，這里僅分析星歷參數擬合誤差的單項影響，計算公式為[27]：

(15)

式中，ΔR，ΔT，ΔN分別為衛星徑向、沿跡和外法向位置分量的擬合誤差；AR，AT，AN分別對應3個方向的貢獻因子。表1列出了利用上述公式計算出的不同高度近圓軌道的URE貢獻因子值大小(用戶最小觀測仰角設為0°)。隨著軌道升高，T方向和N方向的影響逐漸減小，R方向影響逐漸增大。

表1 500～1 000 km高度URE貢獻因子

軌道高度/kmARATAN3000.374 30.655 70.655 75000.455 70.629 40.629 47000.515 30.606 00.606 09000.562 20.584 80.584 81 1000.600 70.565 30.565 31 3000.633 10.547 30.547 31 5000.661 00.530 60.530 620 2000.979 40.142 70.142 7

2 擬合實驗

為了驗證星歷參數模型的適用性，將設計的2種星歷方案用于300～1 500 km高度的低軌衛星軌道擬合。首先對衛星在ECI坐標系下進行復雜力模型下的軌道外推(數據點間隔30 s)，然后采用IERS發布的地球定向參數將軌道數據轉換至ECEF下，外推過程中的攝動力模型設置如表2所示。按照擬合時段長度對實驗數據進行分組，歷元時刻取每組數據的中間時刻。

表2 攝動力模型參數設置

攝動力模型模型參數地球非球形引力WGS84_EGM96① 階數:21?21② 地球半徑r=6 378.1 363 km③ 地球自轉角速度ω=7.292 158 553×10-5 rad/sec大氣阻力大氣密度模型Harris-priester① CD=2.2② A/M=0.02 m2/kg③ F10.7(2016)=150三體攝動太陽、月球① 太陽引力常數: 1.327 122 000 000×1011 km3/sec2② 月球引力常數: 4.902 801 076 000×103 km3/sec2太陽光壓陰影模型:Dual Cone① Cr=1② A/M=0.02 m2/kg

對高度為300～1 500 km、傾角為45°、偏心率為0.001的衛星軌道進行了2種星歷方案的實驗驗證，擬合時長設置為衛星最大可見時間附近的整分鐘數，如圖1所示。

圖1 不同高度衛星的最大可見時間

2.1 方案1星歷擬合實驗

方案1的星歷擬合實驗結果如圖2和圖3所示。

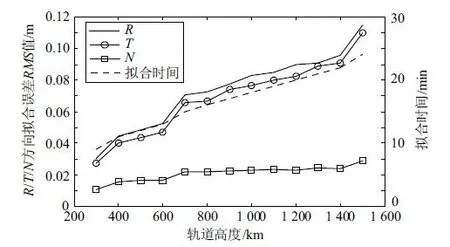
圖2 方案1星歷R/T/N方向擬合誤差統計

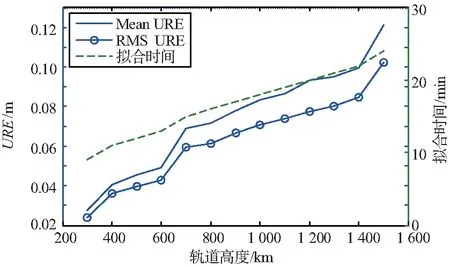
圖3 方案1星歷URE統計

實驗過程中，LEO的擬合成功率均為100%，擬合迭代次數均穩定為3或4次，擬合消耗總時間376 s(處理器：i5-5200U，內存：8 GB)。對于300～1 500 km高度的衛星，隨著軌道高度增加，擬合時間變長，R/T/N三個方向位置分量誤差以及URE都會增大，結合文獻[17]的結論(相同擬合時段條件下，擬合誤差隨軌道升高而減小)可知，導致擬合誤差增大的原因是擬合時間的延長；R/T/N三個方向平均擬合精度分別保持在12/11/3 cm以內，N方向擬合誤差比R，T方向小8～9 cm；URE均方根誤差可以保持在11 cm以內。若要保證星歷URE精度小于10 cm的要求，軌道高度應控制在1 400 km以下。

星歷擬合過程中的900 km高度軌道URE序列如圖4所示。除了個別組URE大于20 cm外，大多數結果波動范圍在0～20 cm。

圖4 方案1星歷URE序列(900 km高度軌道)

2.2 方案2星歷擬合實驗

方案2的擬合實驗結果如圖5和圖6所示。實驗過程中，LEO的擬合成功率均為100%，擬合迭代次數均穩定為3或4次，擬合消耗總時間525 s(硬件配置與方案1相同)。可以看出：R/T/N三個方向擬合誤差分別保持在10/10/3 cm以內；URE的均方根誤差保持在9 cm以內。

圖5 方案2星歷RTN方向擬合誤差統計

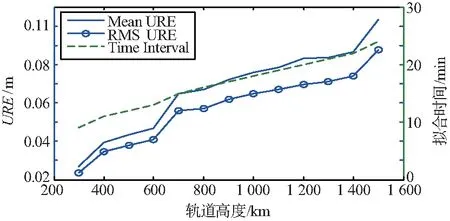
圖6 方案2星歷URE統計

星歷擬合過程中的900 km高度軌道URE序列如圖7所示。URE波動范圍在0～22 cm之間，波動范圍相對于方案1更小，數據集中程度比方案1更高，說明了方案2的算法穩定性更好。

圖7 方案2星歷URE序列(900 km高度軌道)

2種方案的實驗結果表明，方案2星歷擬合精度優于方案1，周期項+常數項能夠更好地擬合低軌衛星攝動力影響，但方案2算法時間復雜度比方案1高。此外，設計的2種軌道列表型16參數星歷模型擬合精度稍優于GPS 16參數星歷模型(GPS 16參數星歷模型精度直接用于低軌衛星擬合10～20 min，精度為分米級[28])。

2.3 IRIDIUM衛星數據擬合實驗

為驗證真實軌道的數據擬合效果，對采用IRIDIUM增強系統的衛星軌道進行了驗證。IRIDIUM系統衛星設計軌道高度為780 km，傾角86.4°，衛星總數66+6(備用)個，均勻分布在6個圓軌道面上。在每個軌道面各取一顆衛星進行實驗，選取2010年3月1-10日共10天的衛星軌道預報數據，力模型設置與前面相同。方案1和方案2的星歷擬合實驗結果如圖8和圖9所示。

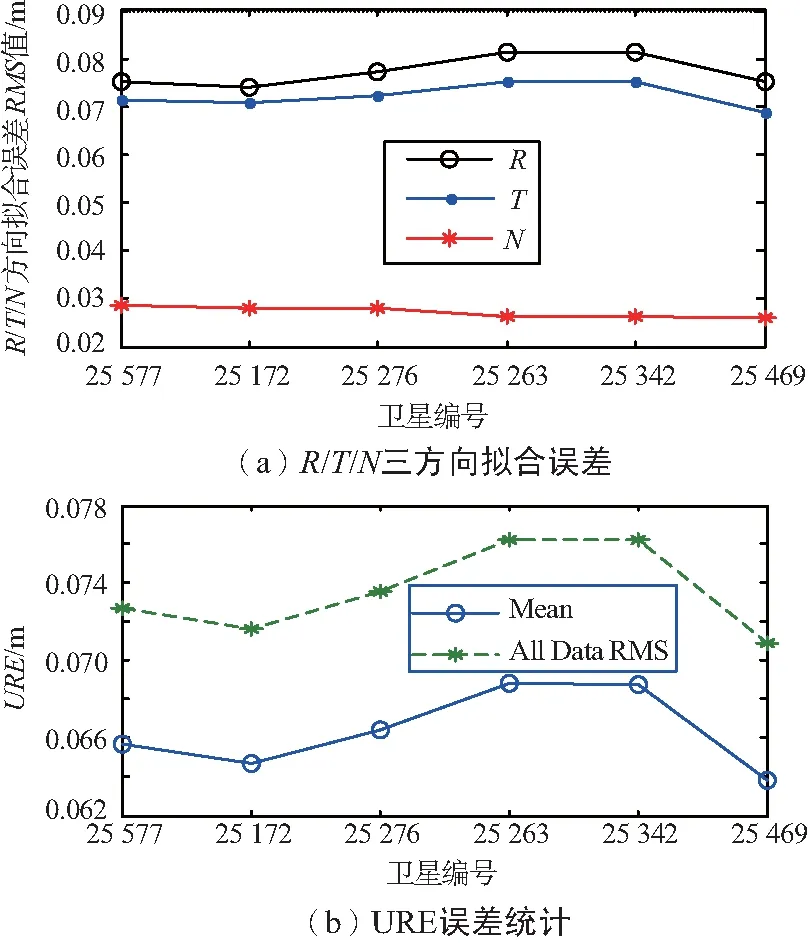
圖8 方案1星歷擬合誤差統計

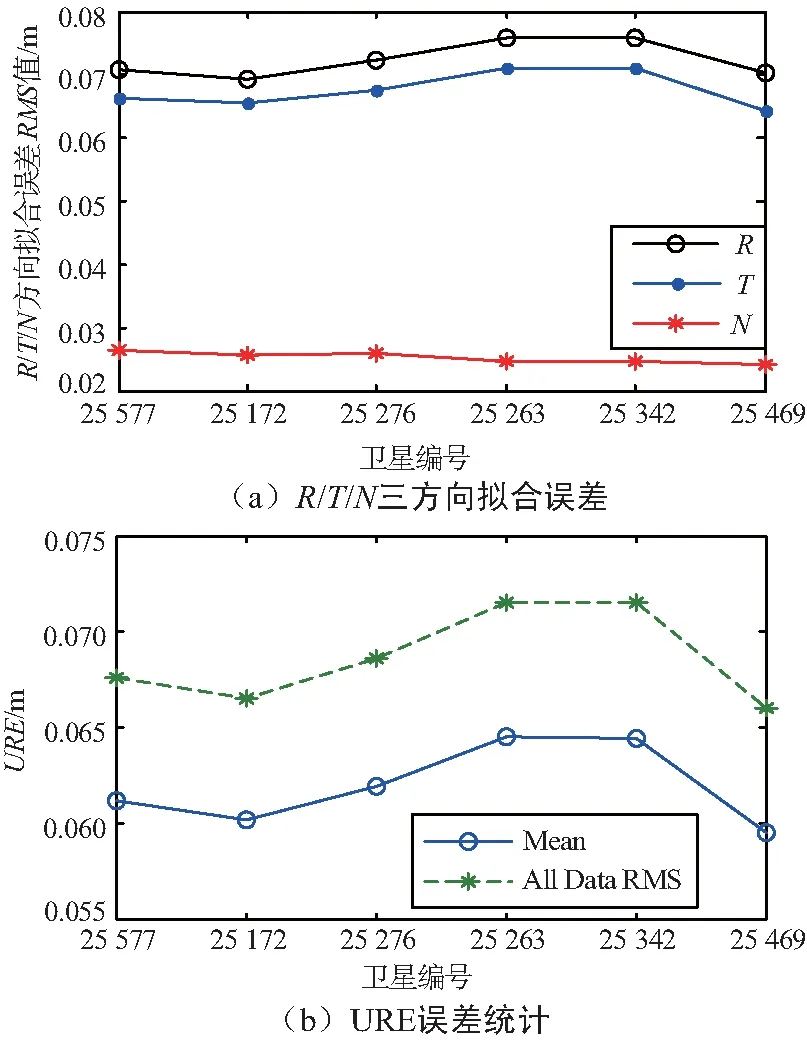
圖9 方案2星歷擬合誤差統計

擬合時間均為16 min(衛星用戶最大可見時間)。實驗過程中，LEO的擬合成功率均為100%，擬合迭代次數穩定為3次。可以看出：方案1中R/T/N三個方向擬合誤差基本保持在9/8/3 cm以內；URE的均方根誤差保持在8 cm以內；方案2中R/T/N三個方向擬合誤差基本分別保持在8/8/3 cm以內；URE的均方根誤差保持在8 cm以內。2種方案擬合結果精度與前面進行的實驗結果精度基本相同，方案2精度稍高于方案1。

3 結束語

針對低軌衛星攝動力的趨勢項和周期項特征，利用二次多項式/周期項+常數項吸收經驗力攝動加速度影響，設計了2種16參數星歷模型。設計的星歷模型具有參數個數少、擬合精度高和無奇點的優點。

基于300～1 500 km高度的LEO擬合實驗表明：① 方案1中R/T/N三個方向平均擬合精度分別優于12/11/3 cm，URE精度優于11 cm。方案2中R/T/N三個方向擬合誤差基本分別優于10/10/3 cm，URE精度優于9 cm；② 2種擬合方案的參數個數相同，方案2擬合精度更高，擬合結果更穩定，但方案2時間復雜度更高。若對時間復雜度有較高要求，建議采用方案1的星歷模型；若對星歷精度有較高要求，建議采用方案2的星歷模型。