在“挑戰難題”的學程中生成新知
——以“三角形中位線性質”教學為例

筅江蘇省海安市海陵中學 魏愛鳳

最近一次教研活動中，筆者有機會執教“三角形中位線性質”，備課過程中幾易其稿，從最初根據教材按部就班地“照本宣科”到“習題題組呈現的變式教學”設計，再到最后基于“問題驅動”式的教學設計，筆者對這節課教學內容的理解也逐漸加深.從課堂實踐來看，也取得了較理想的教學效果.本文先整理該課最后定稿的教學設計，并給出教學立意的闡釋，供研討.

一、三角形的中位線新授課教學設計

1.從數學現實出發，激發學生挑戰興趣

課前，在黑板上先畫出幾個三角形，開課后依次在這些三角形中畫出三條角平分線、三條邊的垂直平分線（如圖1和圖2），學生都能肯定它們交于一點，并且此前都進行過證明.

圖1

圖2

在圖3中，要求學生畫出三邊的中線，大家會發現三邊的中線竟然也能交于一點！如何證明呢？學生挑戰，2分鐘后，教師可告知大家，這個太難了，需要用到平行四邊形的知識，所以之前我們在學習三角形或全等時都沒有涉及這個奇異的性質，這節課我們來一起攻克這個遺留難題.

圖3

2.發現并證明三角形中位線性質定理

問題1：讓我們從平行四邊形出發，如圖4，平行四邊形ABCD中，對角線AC、BD交于點O，延長AB到E，使BE=AB，連接CE.圖中又出現了一個平行四邊形，請大家找出來，并證明.

教學組織：學生很快會證出四邊形BECD為平行四邊形，安排另一個學生復述一下證明思路，不必給出書面表達，因為這不是本課的教學重點，以便節約課堂時間.接下來教師將圖4中有些線段擦去，得到圖5，提出問題：

圖4

圖5

問題2：在△AEC中，B、O分別是邊AE、AC的中點，探究線段BO與CE的數量關系、位置關系.

教學組織：安排學生獨立思考，待學生有思路后教師巡查、交流，然后讓學生分組討論證明思路，最后安排兩個小組派代表上臺講解輔助線的構造與證明思路.多數學生應該能想到轉化為圖4進行證明.

引導歸納：如圖6，△ABC中，D、E分別是邊AB、AC的中點，連接DE，定義線段DE為△ABC的中位線.請大家想想，一個三角形的中位線有幾條，它們與三角形的第三邊有怎樣的關系？你會證明嗎？

教學組織：學生有了前面圖5的證明經驗，很快就可歸納出三角形的中位線性質定理，教師進行板書，并安排學生寫出該定理的符號表示形式.

圖6

3.迎難而上，挑戰難題

過渡：讓我們開始挑戰“三角形三邊中線交于一點”這個難點.與以前證明三角形三條角平分線交于一點類似，如圖7，也先設兩條中線交于一點M，我們試圖證明點M也在第三條中線上.證明思路比較獨特，考慮到今天課堂學習時間有限，老師幫助大家提供一種思路導引，一起來看問題3.問題3：如圖7，BD、CE是三B F C角形ABC的兩條中線，它們交于點M.小晶度量后發現，點M恰是BD、CE一個三等分點.她換了一個圖之后，如圖8，點M′竟然也是中線BD、AF的一個三等分點.你能發現其中的道理嗎？

圖7

圖8

教學組織：提示學生取BM、CM的中點G、H，順次連接點D、E、G、H，利用三角形中位線性質證明四邊形DEGH是平行四邊形，從而可以貫通思路.在圖8中，可以安排學生在小組內交流，再在大組內講解思路，通過學生變換不同圖形（圖7或圖8）連續兩到三次的重復講解，讓更多學生跟上證明思路，加深對任意兩條中線的交點都是中線的一個三等分點的認識，從而確認點M是三條中線的交點，也攻克了開課階段提出的疑難問題.

歸納性質：三角形三條中線交于一點，并且這點恰是中線的一個三等分點.（可以向學生介紹這個點稱為重心，這個性質就是著名的“重心定理”）

4.課堂小結，反饋練習

小結問題1：本課內容主要學習三角形的中位線、中線相關內容，但安排在平行四邊形這一章中，你覺得教材編寫專家為什么這樣安排？

小結問題2：通過本課的學習，你覺得三角形的中線與中位線有什么區別？

小結問題3：關于三角形的中位線和中線的區別，你們說得很好，它們有時也會有“關系”.比如，三角形一條中位線與第三邊上的中線就能互相平分.你們能理解嗎？小組內交流一下如何證明.

反饋練習：如圖9，△ABC中，中線BD、CE交于G點，連接DE.

（1）若BC=5cm，求中位線DE的長.

（2）若CG=10cm時則GE的長為多少？

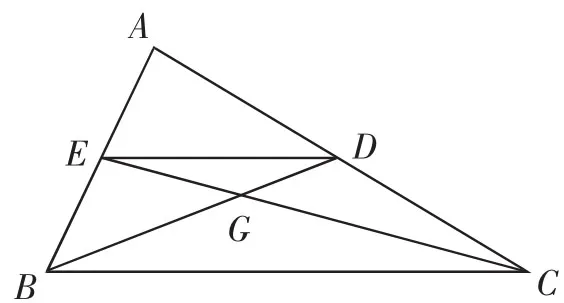
圖9

（3）連接AG并延長交BC于點F，交DE于點M.

①小海認為AF一定是△ABC的中線.你覺得小海正確嗎？（直接回答“正確”或“錯誤”）

②若AF=9cm，求GF的長為多少.

設計意圖：全課沒有安排例題，只在小結之后安排這個題組訓練本課所學習的內容（涵蓋三角形中位線性質、重心性質）.

二、教學立意的進一步闡釋

1.深刻理解教學內容，精選數學現實驅動新課

三角形中位線沒有安排在三角形一章學習的根本原因是：說清或證明它的性質時，結合平行四邊形的性質與判定會更加便捷.將這個疑惑作為一個問題情境激發學生的學習興趣與挑戰欲望，就是一個較為恰當的“數學現實”，并將其作為“問題”驅動新課教學.這類數學現實的選擇需要教師深刻理解教學內容，結合本課教學目標進行優選，而不是“照本宣科”，這也是從“教教材”走向“用教材教”的具體實踐.

2.深刻理解學情、教情，開展“有指導的”新知教學

在教學內容確定之后，還需要結合學情與班情，想清辨明學生對待學內容或相關習題的接受程度，研判學生可能出現的障礙或困惑之處，在此基礎上預設各個教學環節及鋪墊式問題.比如，上文中對于“疑難問題”（求證三角形三邊中線交于一點）在沒有學習過的情況下，在這節課有限的教學時間內是難以快速突破的，所以就引出先研究三角形中位線的性質，進而幫助學生復習、類比三角形三條角平分線交于一點的證明思路，然后啟發學生證明三角形兩條中線交點的性質，這些都是課前鋪墊、預設的，學生在這些“有指導的”教學點撥之后才能順利解決，也能保證在課堂教學時間內完成教學任務.

3.精心預設小結問題，跟進習題訓練反饋學情

本課另一個精心設計之處是幾個“小結問題”，我們沒有用一些“空而泛”的小結問題，如“這節課學到了什么？這節課你有什么收獲”之類的問題，因為這些問題對于引導學生小結這節課所學不夠精準，對本課教學重點、疑難點的辨析也不充分，所以我們讓學生猜想教材編寫者的編寫意圖，也讓學生辨析中線與中位線的區別和聯系，并在此基礎上設計了一組問題串對本課所學的內容進行鞏固訓練，即時反饋學情.

三、寫在后面

這次教研活動的教學設計與磨課經歷讓筆者知道教學即研究，教研無止境，專業精進永遠在路上.面對三角形中位線性質，一年又一年重復教學過很多次，卻仍然有值得深入思考的教研話題，這也啟示我們，面對經典課題的教學，仍然要基于“三個理解”，精心備課，常教常新.想來，這也是“誨人不倦”的職業追求吧.

致謝：本課教學設計、試教打磨的全過程都得到海安市教師發展中心初中數學教研員劉東升老師的精心指導，謹致謝意！