讓數學教師語言更有魅力的幾個招數

筅江蘇省無錫市宜興市范道中學 朱亦珍

筅江蘇省無錫市宜興市紅塔中學 張 躍

一個充滿活力的課堂氛圍，會使學生在知識中探索，做學習的主人，使學習的效果達到最佳的狀態，在這其中，誰起了最大的作用？教師的語言.

教師課堂中的語言往往最重要的是口語表達，數學教師的口語表達也要像語文老師的口語表達一樣，注重抑揚頓挫，注重語氣語調，注重富有情感等.當然，又不完全等同于語文老師的口語表達，畢竟有學科特征.數學學科的口語表達對接數學知識，要講究知識的內在邏輯性，因此要條理清晰；數學更要注重學生思維的進階，因此要注重啟發性，常用疑問的形式來表達；數學又要注重知識的發生過程，因此在引導學生學習時常用推理性的口語表達，使學生理解知識的發生、發展過程.基于此，數學教師一定要用好數學語言這個武器，借助語言表達的工具，引導學生走進數學學習的過程，指導學生徜徉在數學訓練的實踐之中，在學習與實踐中引領學生建構數學知識體系，引發數學基本的思維與形成基本的數學思想.

那么，如何使數學教師的授課語言更有魅力，更能融洽師生關系，獲得學生的支持與配合，讓課堂更有活力、更加精彩呢？

一、嚴密準確、通俗易懂：數學語言在規范性表述中顯示魅力

數學教師的語言不像語文老師那樣一瀉千里，但要清楚明白，不拖泥帶水，要追求準確、規范、簡潔，通俗易懂，化繁為簡.準確是指沒有科學錯誤；規范是指堅持用普通話、吐字清晰；簡約是指干凈利落、抓重點、有的放矢；通俗易懂是指根據學生的心理年齡，講他們能夠接受的話；化簡為繁是指可以把一個復雜的問題解剖成幾個簡單的問題，最后歸結成一個問題.

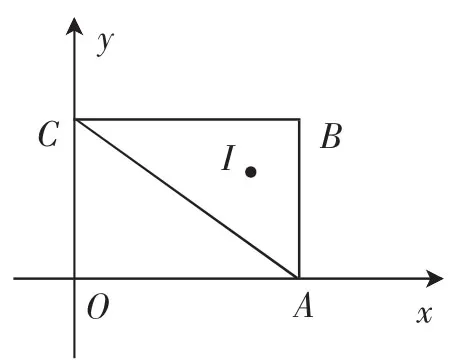
圖1

例1如圖1，在平面直角坐標系xOy中，點A（4、0）、B（0，3）、C（4，3），I是 △ABC的內心，將△ABC繞原點逆時針旋轉90°后，I的對應點I′的坐標為（ ）.

A.（-2，3）B.（-3，2）C.（3，-2）D.（2，-3）

這題是2018年初三期中考試卷中錯誤率較高的一題.

對于例1，我們需要抓住兩個重點：（1）I是△ABC的內心，根據直角三角形內切圓的半徑公式r==1，就能根據圖形得到點I的坐標為（3，2）；（2）繞原點旋轉90°，根據開鎖原理就能得到點I′的坐標（-2，3）.這樣通俗易通，兩步就能解決問題.

平時不注意語言的規范、精煉、導致出現“口頭禪”較多，如：“嗯、哦、是否”等.學生的注意力由聽上課內容變成了統計教師說“口頭禪”的次數.語言的重復、累贅、不規范，不僅浪費了課堂時間，而且影響了學生的聽課效率.

二、設置懸念、精彩提問：用生動、有趣的語言表達來呈現魅力

著名教育家陶行知先生曾經說過：“發明千千萬，起點是一問，智者問得巧，寓者問得笨.”在數學課堂中，教師要靈活運用自己的教學語言激發學生的求知欲望，增強學生的主觀能動性，引導學生主動質疑問題，并多為學生創設情境，制造懸念.例如，在中考專題總復習時，講解“雙子型”這一專題時我是這樣設計的：

圖2

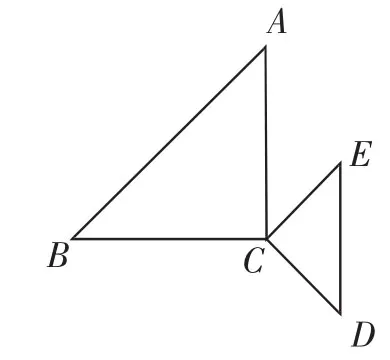
圖3

【全等雙子型】

例2△ABC和△CED均是等邊三角形（見圖2），C點是公共點，請大家仔細觀察這張圖，可以得到哪些結論呢？

常見結論：三角形全等，線段相等，角的結論.

變形1：如圖3，△ABC和△CED均為等腰直角三角形，點C為公共點.你又能得出怎樣的結論？

常見結論：三角形全等，線段相等；角的結論.

變形2：假如我們把兩個等腰直角三角形變換成兩個正方形，仔細觀察圖4，你還能得出怎樣的結論呢？

由此延伸，我們可以由特殊圖形拓展到一般的圖形，如圖5，△ABC和△ADE均為等腰三角形，A點為公共點，且滿足∠BAC=∠DAE.那么，根據你的觀察與思考，又可以得出怎么的結論呢？

常見結論：三角形全等，線段相等，角的結論.

通過上面的探討學習，同學們還有什么疑惑？

這樣用簡潔、通俗易懂的語言不斷創設情境，不斷制造懸念，把學生帶入了數學天地進行自主研究和探討，由一個題目融會貫通了一類題目.學生感受到了數學的好玩，享受到了學習數學的樂趣！

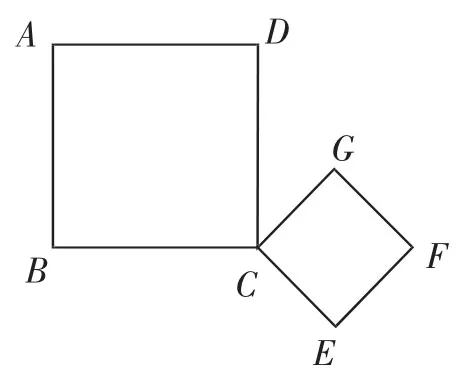
圖4

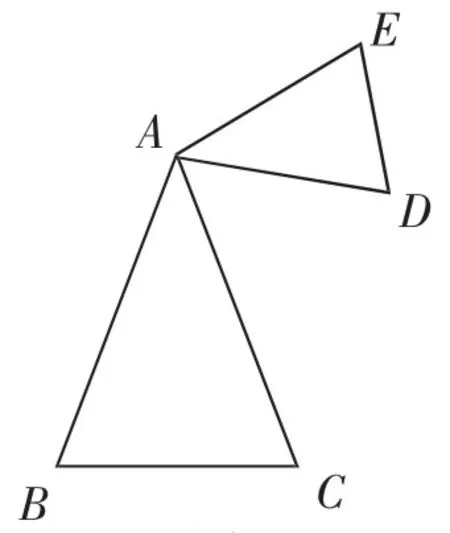
圖5

三、嚴密推理、環環相扣：在完整的、富有推理邏輯性思維的語言表達中彰顯魅力

在數學課堂上，教師在指導學生學習數學知識時，應該對接所要學習的數學知識，用準確的、富有邏輯性的語言引導學生進行數學知識的論證與推理.用嚴密的語言邏輯力量指導學生一步接一步、一環扣一環地進入到數學知識的推理過程中來，也即學習過程中去.因此數學教師在課堂上的引導語言應該注重條理的清晰性、推理的嚴密性，力求做到通順、連貫、得體，否則學生的思維就很難進入到知識的邏輯鏈中去，思維能力就得不到提升.同時，教師的課堂教學語言要注重高度的概括性，引導學生在自主學習探究中概括提煉知識推進中的規律，便于學生知識的建構！

例3在等腰梯形ABCD中，AD∥BC，AB=CD=AD.∠C=60°，E、F分別在AD、CD上，DE=CF，AF、BE交于點P.

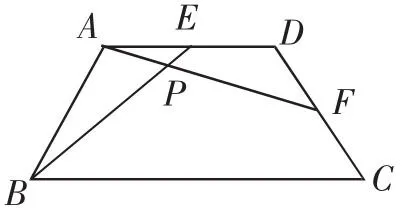
圖6

（1）AF與BE相等嗎？為什么？

（2）請你猜測∠BPF的度數，并說明理由.

解析：（1）答：AE=BF.

由AB=CD=AD，DE=CF（已知），得AE=DF（等式性質）.

由四邊形ABCD為等腰梯形（已知），得∠BAE=∠D（等腰梯形的性質）.

則△ABE △DAF（SAS）.

則AF=BE（全等三角形的對應邊相等）.

（2）由△ABE △DAF（已證），得∠ABE=∠DAF（全等三角形的對應角相等）.

又∠APB=∠DAF+∠AEB（外角定義），∠APB+∠BPF=180°（平角定義），∠ABE+∠AEB+∠BAE=180°（三角形內角和定理），則∠BPF=∠BAE（等式的性質）.

在等腰梯形ABCD中，AD∥BC（已知），則∠DAB+∠ABC=180°（平行線的性質）.

又∠C=∠ABC=60°（已知），則∠BPF=∠BAE=120°（等式的性質）.

這樣一步接一步，有理有據，有條不紊，一環緊扣一環，論證嚴密，無懈可擊，教師在語言表達上讓學生感受到了數學的理性之美──隱含著一種完整的合理的邏輯推理.

四、抑揚頓挫、和諧悅耳：語言在富有音樂般的催人奮進的效果中表達魅力

古人說：“感人心者，莫先于情.”我們都知道，富有激情的語言才有誘惑力，才能激發學生的學習興趣和探求知識來龍去脈的動機，學生在強烈的求知欲的刺激下，思緒才能凝聚，思想才能高度集中，學習的過程才能真正呈現，而不致于使學生“身在曹營心在漢”.那么怎樣才能達到上述目的呢？

首先，要做到抑揚頓挫，和諧悅耳.要依據教學內容，結合其中隱含的知識點，有目的地用高音呈現，這樣不僅可使學生聽得更清晰，也使得分神的學生回聚身心；其中較難的知識點或學生思維跟不上的地方，我們可以做略微的停頓，這樣做，可以讓學生多思考一會，以便能理解通透，也可以使思維速度慢的學生跟上大家的步伐；對比較重要的教學內容，教師可以用一些不同于往常的語氣、語調，以讓學生感到不同而更專注聆聽與思考.

其次，要做到聲情并茂.我們知道，教師的語言一旦平鋪直敘，就會顯得平淡無奇，因此數學教師更要善于利用教學內容，結合自己的體態語言，尤其是面部表情，使面部表情與語言深度融合，使學生覺得教師的教學語言更和藹可親.

五、幽默詼諧、精神愉悅：在啟發性語言的“誘惑”中凸顯語言表達的魅力

生動形象、幽默詼諧的語言能直抵學生的心靈深處，更深層地激起學生的學習興趣.幽默感強的教師只要走進課堂，走到學生中間，學生就會感到親切快樂，師生之間的“教”與“學”的互動就會自然產生，所以這樣的老師上課，課堂氣氛就會活躍而熱烈，學生在學習時就會消除疲勞和緊張，始終使大腦保持興奮，從而達到寓教于樂的目的.例如，在講到科學記數法四舍五入時，我引入這樣一個故事：一天明明哼著小歌從學校里回來，問媽媽：“爸爸呢？”媽媽看到明明開心的樣子，奇怪地問：“爸爸在家，你找爸爸做什么？”“我向爸爸要50元錢.”“為什么？”媽媽問道“.在考數學以前，爸爸對我說‘如果考了100分，就給我100元錢，考90分給90元.’今天，我數學考了45分.”明明回答說.媽媽吃驚地問：“什么！數學才考45分？”明明得意地說：“是呀，數學上要‘4舍5入’，因此，爸爸必須付50元錢.”一講完，學生就哄堂大笑，學生的注意力一下子被我吸引過來了，同時他們在這快樂的氣氛中學會了這個理論.

數學作為一門邏輯性要求高的學科，在教學語言上也要有相應的特點.生動的語言會使一節枯燥乏味的課富有活力；真誠的語言會使學生投入到情境中去；幽默的語言會吸引學生的注意力從而體會到學習的快樂.數學教師的語言要富有魅力，更要注重語言表述的準確、規范、科學、富有邏輯性，這樣學生就可以在數學語言魅力的感召下學有興趣、學有所得、學有提高、學有效率、學有創意、學有追求；在數學學習中就能走向自主學習、自能學習，逐漸走向數學學科核心素養的自我構建.