一類四階與六階微分算子積的自伴性

林秋紅

(廣東理工學院基礎部，廣東 肇慶 526100)

引 言

近兩年，關于微分算子自伴性問題的相關研究得到很多關注。文獻［1］給出了4 階正則微分算子耦合自共軛邊界條件的基本標準型，為給出一般高階微分算子自共軛邊界條件標準型提供了新思路; 文獻［2］研究了J-對稱微分算式在兩端奇異且虧指數不相等時J-自伴擴張的邊條件問題;文獻［3］討論了二維向量空間中二階微分算子在兩區間上的自伴擴張問題。

此外，關于微分算子乘積或冪的自伴性研究也一直受到許多學者的關注，特別是對同階微分算子乘積的自伴性研究，已有較多的研究成果。1996年，邊學軍［4］研究了二階自伴微分算子ly = －y″ +q(x) y 所生成的冪算子的自伴性;1999年，曹之江、孫炯等［5］研究了正則和奇異兩種情況下二階微分算子的積算子自伴性，得到了積算子為自伴算子時其邊條件應滿足的充分條件; 2006年，張新艷等［6］討論了正則和奇異的2n 階微分算子的積算子自伴性，得到了積算子自伴的充要條件。2010年，楊傳富等［7-8］研究了兩個四階微分算子的積的自伴性，并得到了兩個四階微分算子積的自伴的充要條件，并進一步給出了m 個微分算子乘積自伴的條件; 張新艷、王萬義等［9-10］利用自伴算子的基本理論及矩陣運算，討論了三個二階微分算子積的自伴性，并進一步討論了三個高階微分算子積的自伴性;2014年，鄭召文、劉寶圣［11］給出了在極限圓型時判定三個Hamilton 算子乘積自伴的一個充要條件。但上述這些研究都只是針對同階微分算子的積算子自伴性的研究。

2016年，文獻［12］利用矩陣運算，討論了一類二階與一類四階生成的兩個微分算子積的自伴性問題，并在常型情形下，得到積算子自伴的充分條件。自此，對于兩個不同偶數階的微分算子積自伴性便沒有得到更多的研究。

本文將利用新的方法繼續研究一類四階和一類六階的微分算子積的自伴性問題，并得到了積算子L =L1L2為自伴算子的一個充要條件，有趣的是這個充要條件和同階的微分算子積算子自伴的充要條件有著相似的結構，這為進一步研究一般的兩個不同偶數階微分算子自伴性提供了研究思路。

1 預備知識

設:

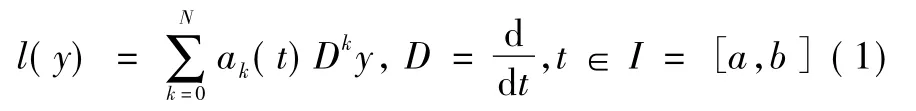
為區間I 上具有適當可微復值函數系數ak(t) 的N階微分算式，若aN(t) 不等于零，則稱l(y) 正則。以l*(y) 表示l(y) 的共軛算式，即若l(y) ≡l*(y) ，則稱l(y) 為對稱微分算式。

設［·，·］N表示l(y) 的Lagrange 雙線性型，有格林公式為:

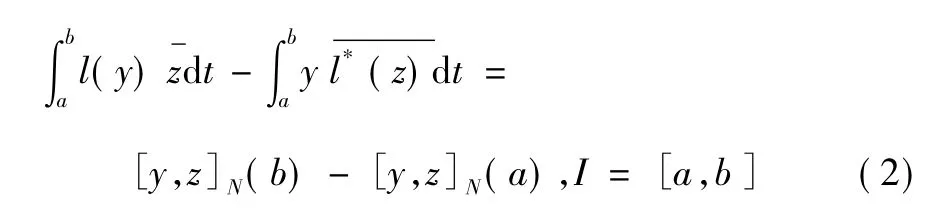
本文記n 行m 列矩陣A = (aij)n×m，(i =1，2，…，n;j = 1，2，…，m) 。特別是n = m 時，簡記A = (aij)1≤i，j≤n。AT及A*分別表示A 的轉置及共軛轉置，AO表示A 的全轉置; 0，0n，In，R 分別表示零向量，n × n 零矩陣，n × n單位矩陣及實數集合; (M ⊕N) 為m × (m + n) 矩陣，其前n 列由M 組成，后n 列由N 組成;表示復數a 的共軛復數。設QN(t) 表示雙線性型相應的矩陣，則:

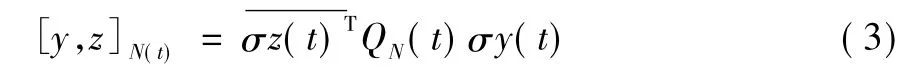
這里:

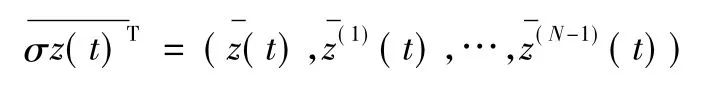
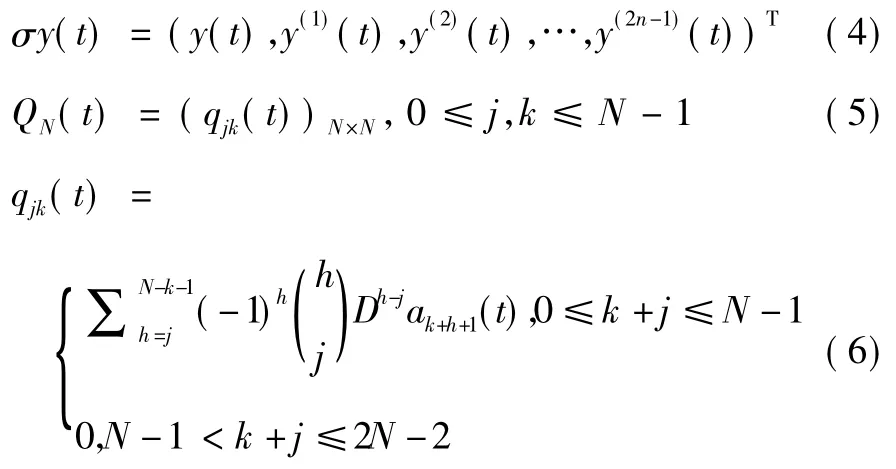
由于實對稱微分算式階數為偶數，設:

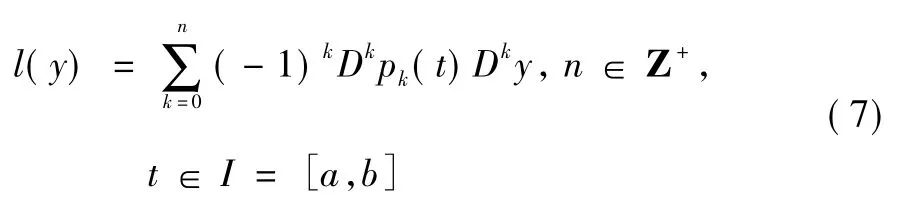
這里實函數pk(t) ∈C2n+k(I) (k = 0，1，2，…，n) ，

記LM為由l 生成的最大算子，其定義域為:

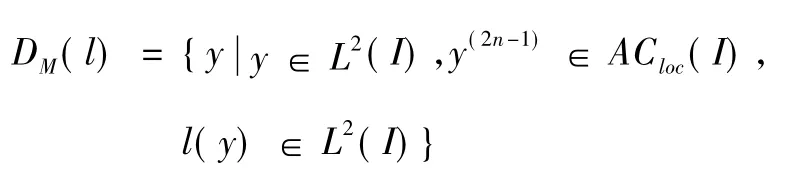
而由l 生成的最小算子記作L0，它是算子LM限制在上所得算子的最小閉延拓，即:記其定義域為D0(l) 。

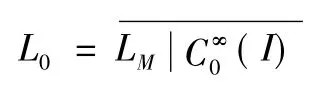
為了證明主要結果，需要下列預備知識。

引理1［13］函數y ∈D0(l) 的充要條件為:

(1) y(0) = y(1)(0) = … = y(2n－1)(0) = 0 ;

引理2［7］設A，B，C 為n × n 矩陣，B，C 可逆，則可逆，且:

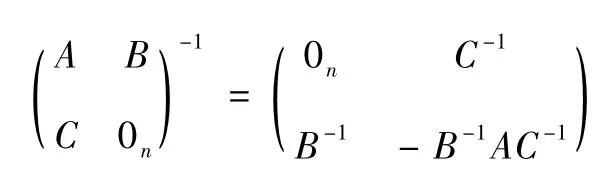
引理3［14］設l(y) 是定義于區間I = ［a，b］的2n階正則對稱微分算式，由l(y) 生成的微分算子L 是自伴算子的充要條件為:存在2n × 2n 數量矩陣M，N 使得L的定義域為:

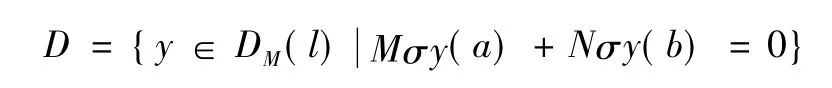
這里σy(a) ，σy(b) 定義于式(4) ，且:

(i) Rank(M ⊕N) = 2m +2n;

定義1［15］設:

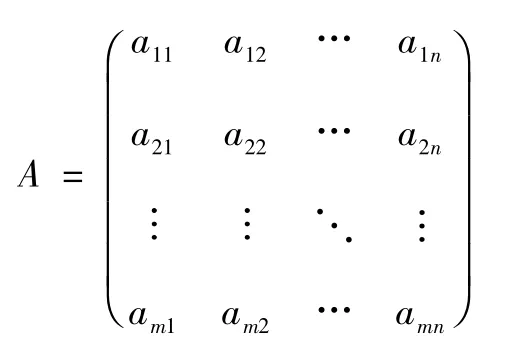
將A 順時針(或逆時針) 旋轉180 度，得到矩陣稱為矩陣A 的全轉置矩陣，記為AO，并記:

2 微分算子積的自伴性

設:

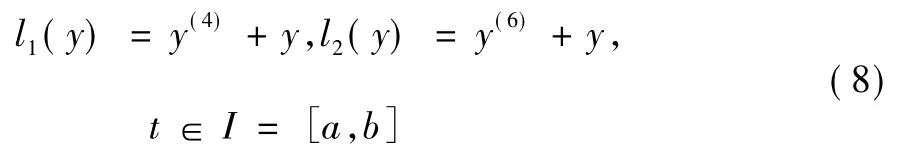
由式(5) 和式(6) 計算得到微分算子l1(y) ，l2(y)的Lagrange 雙線性型矩陣Q1和Q2為:

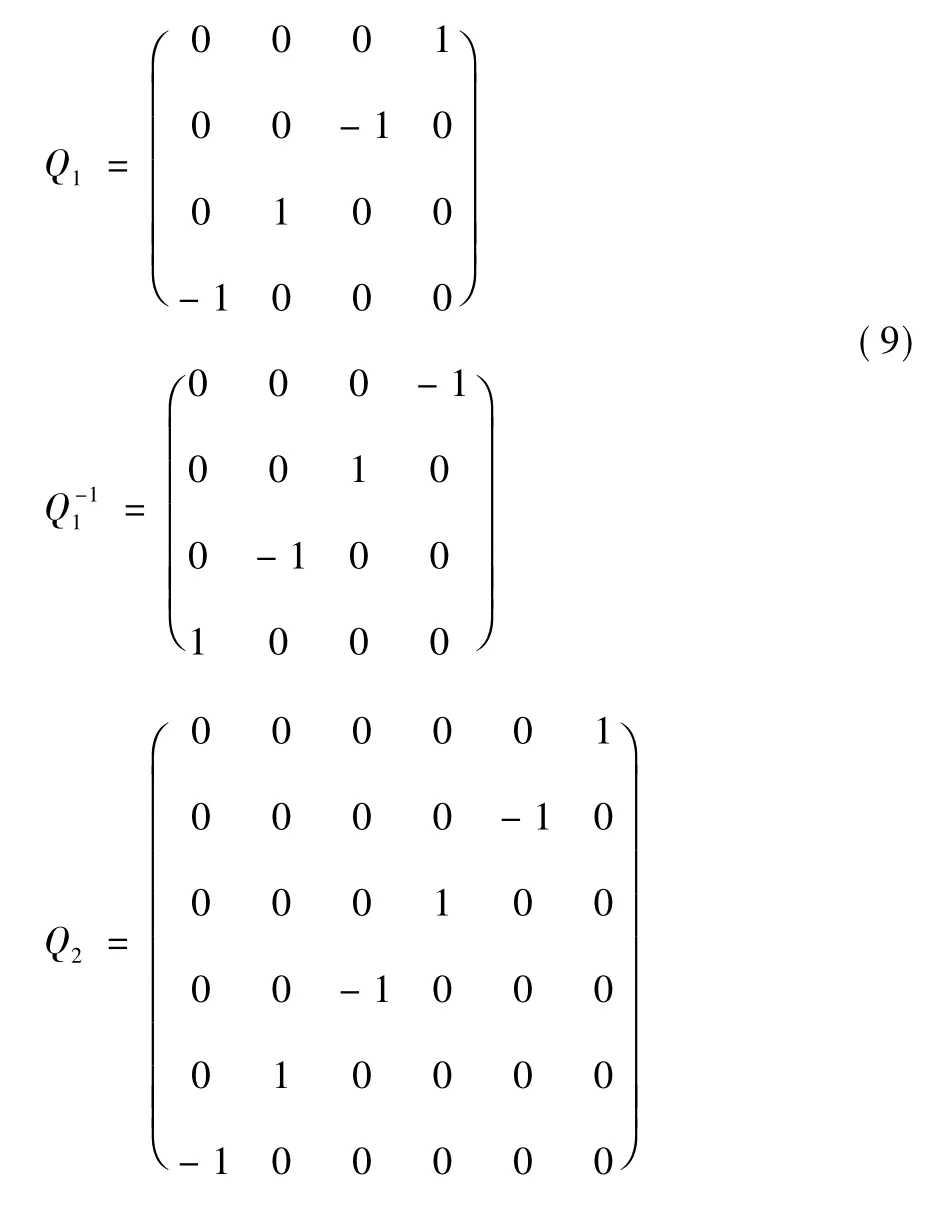
定義微分算子Li(i = 1，2) 如下:

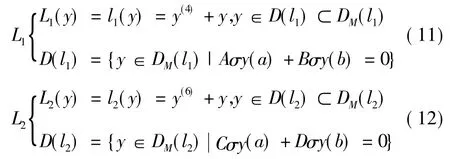
這里，σy(t) = (y(t)，y(1)(t)，y(2)(t)，…，y(2n－1)(t) )T;A，B 為4 ×4 數量矩陣; C，D 為6 ×6 數量矩陣。且:

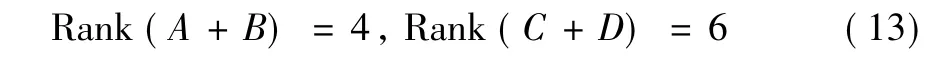
不失一般性，令:

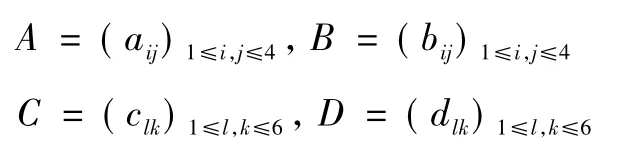
其中aij，bij，clk，dlk∈R(i，j = 1，2，3，4;l，k = 1，2，…，6) 。

設:

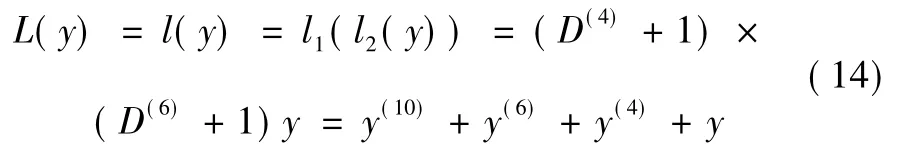
其Lagrange 雙線性型矩陣為Q10，則由式(6) 及引理2得:

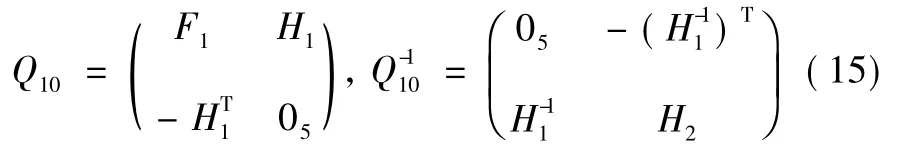
其中:

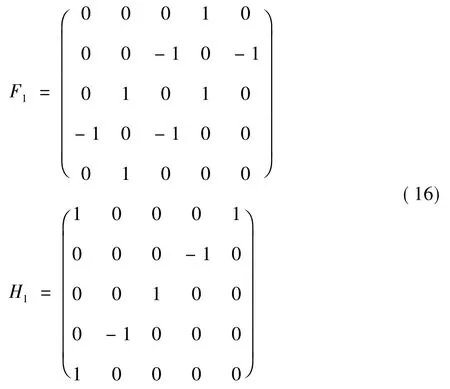
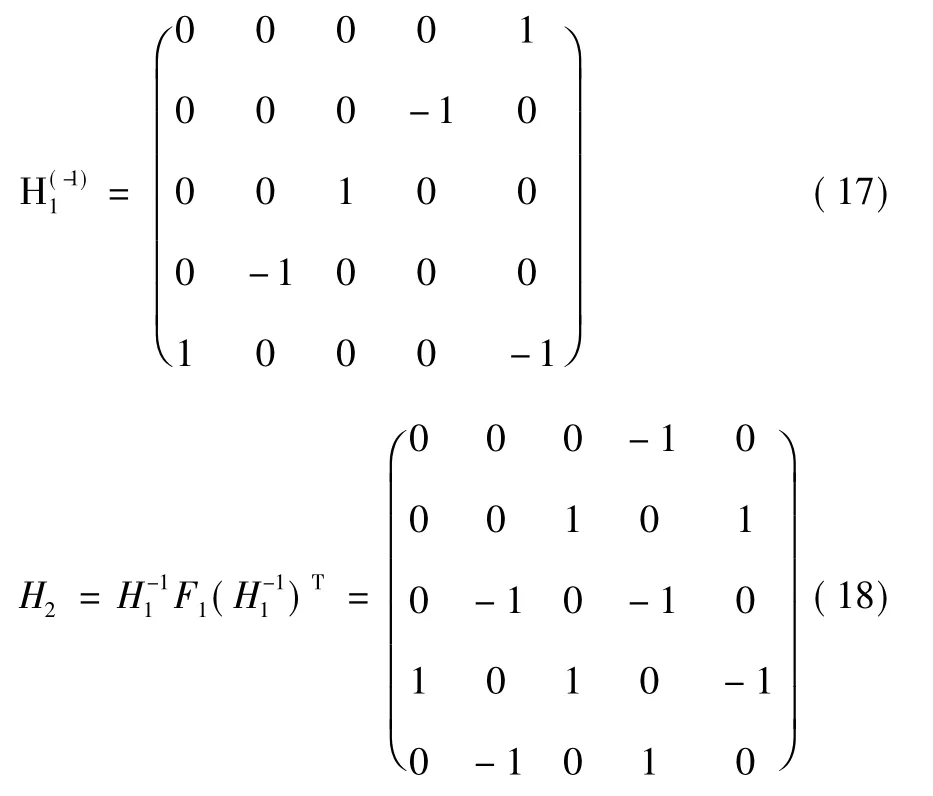
由式(8) 直接計算可得:

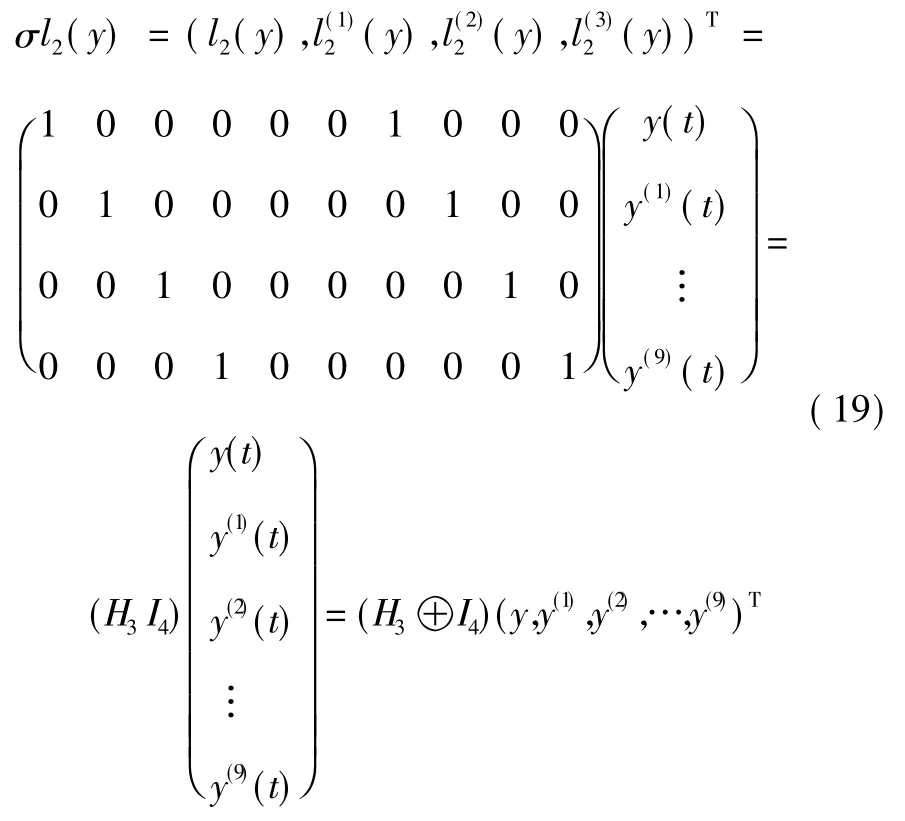
其中:

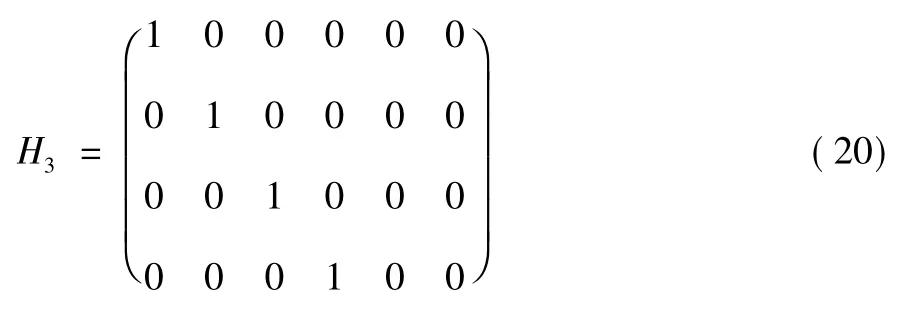
按照積算子L(y) = L1L2(y) 的定義，L(y) 的定義域是:

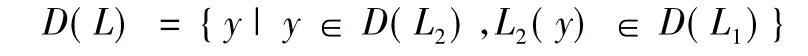
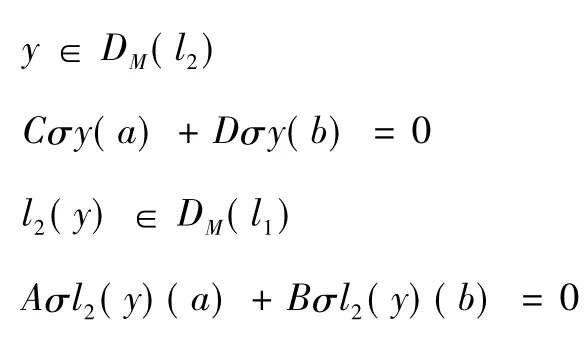
故由式(19) 得:

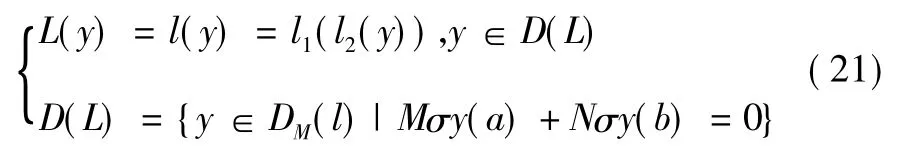
其中:

定理1Rank(M ⊕N) = 10

證明由于:

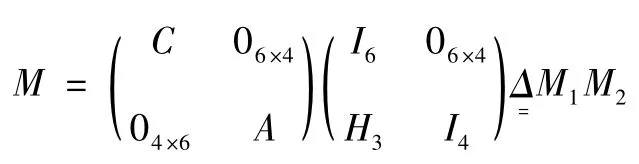
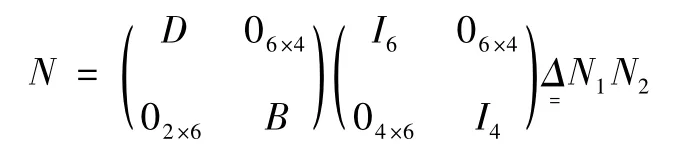
則:

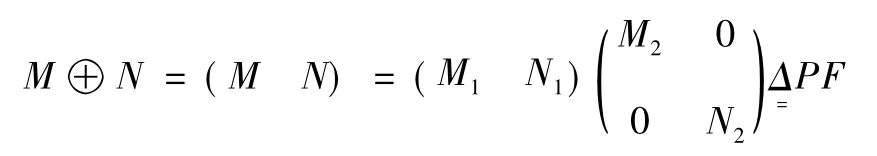
而det(F) = det(M2) ，det(N2) = 1 ×1 = 1 ≠0，即F 是可逆的，所以根據矩陣知識可知: Rank(PF) =Rank(P) = 10，即Rank(M ⊕N) = 10，證畢。

定理2積算子L = L1L2自伴的充要條件為:

CS(a) A*= DS(b) B*

證明由于L 是10 階實對稱微分算子，根據引理3和定理1，只須證明:即可，其中同上。事實上，由式(15) 、式(22) 及引理3 可知:

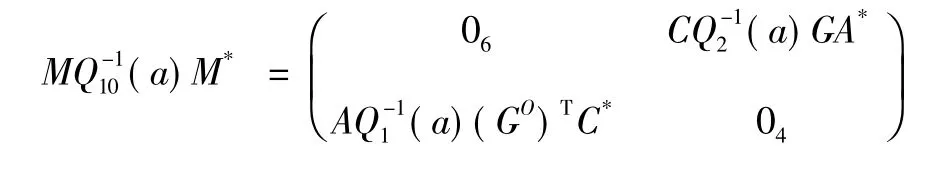
其中:

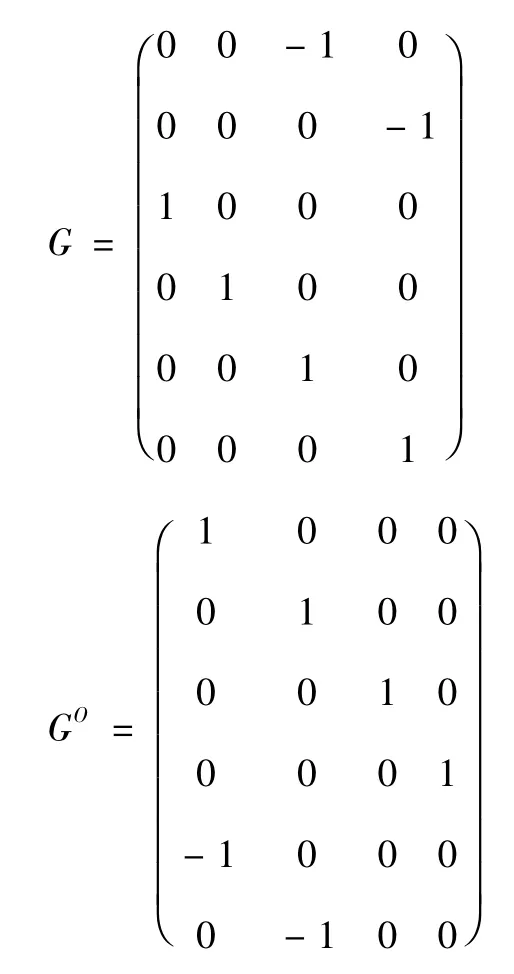
為矩陣G 的全轉置矩陣。

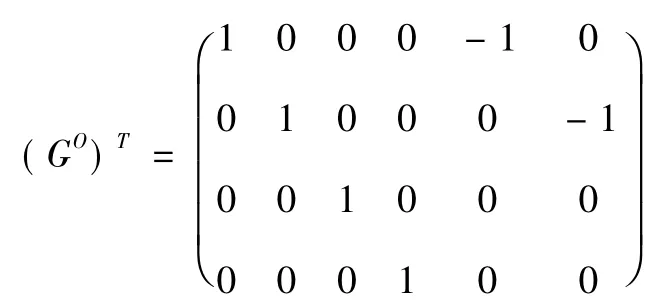
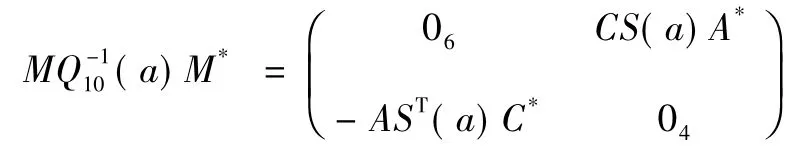
同理可知:

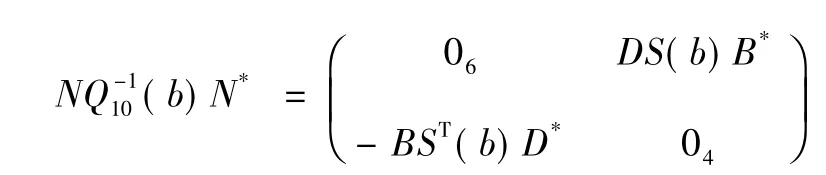
用相同的方法，可以進一步研究任意2 n 階微分算子與2 m 階微分算子的積算子自伴性。