廣義拓撲空間中濾子的一些結果

郭 俊，朱培勇

(電子科技大學數學科學學院，四川 成都 611731)

引 言

2002年，匈牙利數學家Csaszar A［1］提出廣義拓撲空間，并對其作了較深入的研究，初步取得了一些成果。在此基礎上，Csaszar A 及其他學者對一般拓撲進行了類比，在廣義拓撲空間的點集理論、映射性質方面取得了一系列成果［2-7］。2014年，王鑫等人［8］得到了廣義拓撲與強廣義拓撲之間的一些聯系，并在強廣義拓撲定義的基礎上，得到了一般拓撲中所具有的一些遺傳性質。2015年，李陽［9］探究了廣義拓撲空間中五類廣義開集之間的關系。2016年，李陽等人［10］進一步探究了廣義拓撲空間中的開集與連續性。2017年，Sun W H 等人［11］引入了廣義拓撲空間中的單調正態性，給出了μ-單調正規空間的刻畫和幾個保守定理，而且建立了μ-單調正規空間的Urysohn 引理的“單調變體”。

基于上述成果，提出以下問題: 是否可以類比一般拓撲，在廣義拓撲空間中引入濾子概念，并且得到關于濾子的一些性質和理論結果?

本文主要就上述問題，在文獻［1］的基礎上對廣義拓撲空間中的濾子進行研究，并得到廣義拓撲空間濾子的一些結果;并且，將廣義拓撲空間濾子與映射相結合，獲得濾子和映射的一系列結果。

1 預備知識

首先，回憶廣義拓撲空間的概念:

定義1［1］X 是任一非空集合，T 是X 的一些子集構成的集族，則稱T 為集合X 上的一個廣義拓撲，如果下列兩個條件被滿足:

(A1) 若{Gλ}λ∈Λ∈T 。

這時稱有序偶(X，T ) 為一個廣義拓撲空間，集族T 中的每一個元都稱為該廣義拓撲空間的廣義開集。下面是與廣義拓撲相關的一些概念［12］:

此外，所有沒有定義的關于拓撲空間的概念、術語和記號，如果沒有特殊聲明都選自文獻［13］。在不引起混淆的情況下，也將廣義開集、廣義閉集等稱為開集、閉集等。

下面是濾子的定義及其相關概念的一些介紹。

定義2［14］設F 是集合X 的非空子集族，稱F 是濾子，如果滿足下列三個條件:

(B2) 若A，B ∈F ，則A ∩B ∈F ;

此外，如果X 的子集族G 只滿足(B1) 與(B2) 兩條，則稱G 是一個濾子基;設F 是X 中的濾子，如果不存在真包含F 的濾子，則稱F 為極大濾子。

定義3［14］設F 是廣義拓撲空間X 中的濾子，x ∈X。

定義4設F 與P 是廣義拓撲空間X 中的兩個濾子，f: F →P 是一個映射。A ∈F ，稱映射f 關于A 連續，如果使得f(G)如果關于F 的每個集合都連續，則稱映射f 關于F連續。

定義5設F 與P 是廣義拓撲空間X 中的兩個濾子，f: F →P 是一個映射。

(D2) 若B 是F 中的集合，且B 是閉集，有f(B) 是P 中的集合，且f(B) 也是閉集，則稱f 是閉映射。

下面就關于濾子在廣義拓撲空間中的研究得出的一些結論。

2 廣義拓撲空間中關于濾子的幾個性質

根據濾子聚點的定義，可以得到如下三條等價結論。

定理1X 為廣義拓撲空間，x ∈X，F 是X 中的一個濾子，則下列三條結論等價:

(E1) x ∈ad*F ;

證明

接下來研究極大濾子的廣義聚點集與廣義極限點集的一致性。

定理2設F 是廣義拓撲空間X 中的濾子，若F 是極大濾子，則lim*F = ad*F 。

證明及由F →*x得，使于是由濾子的定義，得因為而U，F ∈F ，所以由定理1 知x ∈ad*F 。即證得

推論1設F 與P 是廣義拓撲空間X 中的濾子，則:

證明

(F1) :由濾子廣義極限定義可知這是顯然成立的。

定理3設X 為廣義的Hausdorff 空間，則X 中每個濾子的廣義極限點唯一;反之結論不真。

反之推不出來。舉例: 設X = {a，b，c}，取子集族顯然有(X，T ) 是一個廣義拓撲空間，取廣義拓撲空間X 中的濾子F ={{a}，{a，b}，{a，b，c}}。假如X 不是廣義Hausdorff 空間，則使UT(y) ，都有b}，{a，b，c}，}UT(y) = UT(b) = {{b}，{a，b}，{b，c}，{a，b，c}}，由于U，V 的任意性，不妨取U = {a，b}，V = {b}，則U所以反之不成立。

3 廣義拓撲空間中濾子與映射連續的關系

引理1設F 為廣義拓撲空間X 中的濾子，A ∈F是開集，當且僅當BA 時，A 是B 的廣義鄰域。

引理2設A 是廣義拓撲空間X 的子集，則:

下面討論連續映射的等價刻畫。

定理4設F 與P 是廣義拓撲空間X 中的兩個濾子，f: F →P 是一個映射，則下列條件等價:

(J1) f 關于F 是連續的;

(J2) 對P 中任意閉集A，f－1(A) 是F 中閉集;

證明

下面討論開映射的等價刻畫。

定理5設F 與P 是廣義拓撲空間X 中的兩個濾子，f: F →P 是一個映射，則下列條件等價:

(K1) f 是開映射;

證明

4 廣義拓撲空間中濾子的推廣

首先介紹濾子在網領域上的一些應用。

在拓撲空間中，網與濾子有著密切聯系，即給定一個濾子就有相伴的網，反過來給定一個網也有相伴的濾子，類比引入廣義拓撲空間中的濾子與網的關系。

設F 是廣義拓撲空間X 中的濾子，令

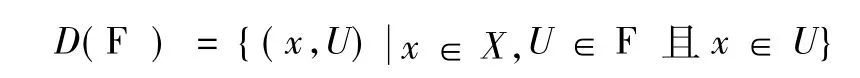
規定D(F ) 的序關系:

由濾子和網的相伴性可以得出濾子廣義聚點、廣義極限點和網聚點、極限點的關系，而且網在黎曼積分中也有應用，具體可參見文獻［15］。

從廣義拓撲空間的定義不難看出，廣義拓撲的條件僅僅取了拓撲條件的一半。因此，廣義拓撲實際上是一類半拓撲，有時也稱其為上半拓撲(Sup-Semi-Topology) 。例如文獻［16］稱廣義拓撲相對于拓撲的另一半條件的集族為下半拓撲(Inf-Semi-Topology) ，具體如下:

定義6［16］X 是任一非空集合，T 是X 的一些子集構成的子集族，稱T 為集合X 上的一個下半拓撲，如果下列兩個條件被滿足:

(L1) X ∈T ;

(L2) 若G1，G2∈T ，則G1∩G2∈T 。

這時稱有序偶(X，T ) 為一個下半拓撲空間，集族T 中的每一個元稱為下半拓撲空間(X，T ) 的下半開集。

用完全類似的方法，可以證明本文的所有結果(除定理3 外) 在下半拓撲空間也成立。而且每個下半拓撲的全部非空元都構成一個濾子，但是每個廣義拓撲的全部非空元就不一定構成濾子，例如:

設(X，T ) 為廣義拓撲空間，其中非空集合X ={a，b，c}，T = {，{a，b}，{b，c}{a，b，c}}，則可F ={{a，b}，{b，c}，{a，b，c}} 不是廣義拓撲空間X 上的濾子。因為不滿足濾子定義2 的第二個條件(B2) 。

5 結束語

本文以一般拓撲為基礎，借鑒近年來研究半拓撲的思想與方法，類比一般拓撲空間中濾子的研究，把拓撲空間中的濾子引入到廣義拓撲空間中進行討論。經過本文的討論和證明可以看出，濾子在廣義拓撲空間中也有廣義聚點、廣義極限點、映射連續等的一些結論成立。而且還將濾子的研究進一步推廣到下半拓撲空間中，也獲得了類似結論。從而可以知道拓撲空間中的濾子性質其實就是一類半拓撲性質。