基于ARIMA和ARCH模型的上海出口集裝箱運價指數短期分析與預測

李志斌 王瀛幟 李柯男 涂貴輝

摘? 要：上海出口集裝箱運價指數（SCFI）是反映市場運價指數行情變化趨勢的主要指標。本文首先運用ADF檢驗對SCFI序列進行檢驗，得出SCFI序列是一個單位根過程，是非平穩的;然后，對SCFI 序列進行一階差分，差分后是平穩的，通過構建ARIMA模型，得出SCFI的ARIMA（2，1，2）模型。針對SCFI指數的波動性，研究其對數序列ln（SCFI），通過ADF檢驗判斷ln（SCFI）序列也是一階單整的。最后，運用ARCH LM檢驗得出SCFI對數序列存在ARCH效應，并用ARCH （1，1） 模型消除殘差序列的條件異方差性。利用Eviews軟件和Crystal ball進行實踐操作，對研究問題進行求解，旨在了解上海出口集裝箱運輸市場形式，判斷市場走向，為相關港航企業經營決策以及政府部門調控管理提供參考。

關鍵詞：上海出口集裝箱運價指數;ADF檢驗;ARIMA模型;ARCH模型

1 緒 論

1.1 研究背景

上海是國際知名的貿易物流中心，位于東南沿海，地理位置優越，鄰近國際航運主干道，適宜建設港口，依托長三角作為經濟腹地，每年都有大量的集裝箱貨物完成進出口貿易。上海港理所當然地承擔起集裝箱進出口樞紐的責任，近些年的集裝箱吞吐量在世界范圍內名列前茅，從2010年起到2018年，已經連續9年坐穩全球第一的寶座。

為更好地反映上海的集裝箱運輸市場水平，上海出口集裝箱運價指數（SCFI）由此而生，通過分析運價指數的影響因素以及波動情況，可以更好地了解運輸市場的價格趨勢，控制價格水平，使集裝箱運輸市場平穩良好地發展，最大限度地發揮運價指數的指導性作用，為我國航運企業提出運價參考，增強上海在建設國際航運中心的競爭優勢，乃至對于推動上海國際航運中心建設具有重大戰略意義。

1.2 研究內容

本文的主要內容：第一章介紹了研究SCFI的背景，基于國內外對BDI，CCFI的研究現狀，確定了本文的研究思路以及研究方法。第二章對研究所用到的理論基礎進行陳述，介紹了單位根檢驗、ARIMA模型、ARCH模型。第三章展示收集到的2011年-2018年的相關數據，對數據本身進行基本的統計性描述，并初步進行處理。第四章應用ARIMA模型和ARCH模型對SCFI進行實證分析。最后對本文的研究成果進行總結以及對未來研究方向的展望。

2 理論基礎

2.1 單位根檢驗

單位根檢驗是判斷一組時間序列是否穩定，這個穩定的標準就是不存在單位根，單位根檢驗就是檢驗序列中是否存在單位根。

（1）DF檢驗

（2）ADF檢驗

在DF檢驗中，實際上是假定了時間序列是由具有白噪聲隨機誤差項的一階自回歸過程AR（1）生成的。但在實際檢驗中，時間序列可能由更高階的自回歸過程生成的，或者隨機誤差項并非是白噪聲，為了保證DF檢驗中隨機誤差項的白噪聲特性，Dicky和Fuller對DF檢驗進行了擴充，形成了ADF（Augment Dickey-Fuller）檢驗。

2.2 ARIMA模型簡介

ARIMA（p，d，q）稱為差分自回歸移動平均模型，指將非平穩時間序列轉化為平穩時間序列，然后將因變量僅對它的滯后值以及隨機誤差項的現值和滯后值進行回歸所建立的模型。p為自回歸項，q為移動平均項數，d為時間序列成為平穩時所做的差分次數。ARIMA模型定義如下：Φ（B）∨dXt=Θ（B）εt 其中Φ（B）為自回歸系數多項式;Θ（B）為滑動平均系數多項式，∨為差分算子，B為滯后算子。ARIMA模型在經濟預測過程中既考慮了經濟現象在時間序列上的依存性，又考慮了隨機波動的干擾性，對經濟運行短期趨勢的預測準確率較高，是近年應用比較廣泛的方法之一。

2.3 ARCH模型簡介

ARCH模型稱為自回歸條件異方差模型，主要用來描述金融數據的波動性（方差變化）。ARCH模型的基本思想是在以前的信息集下，某一時刻一個噪聲的發生是服從正態分布的，該正態分布的均值為0，方差是一個隨時間變化的量即為條件異方差，并且這個隨時間變化的方差是過去有限項噪聲值平方的線性組合即為自回歸。這樣就構成了自回歸條件異方差（ARCH）模型。對于一個時間序列而言，在不同時刻可以利用的信息不同，而相應的條件異方差也不同，利用ARCH模型，可以刻畫出隨時間而變異的條件方差。

3 相關數據及處理

3.1 數據選取

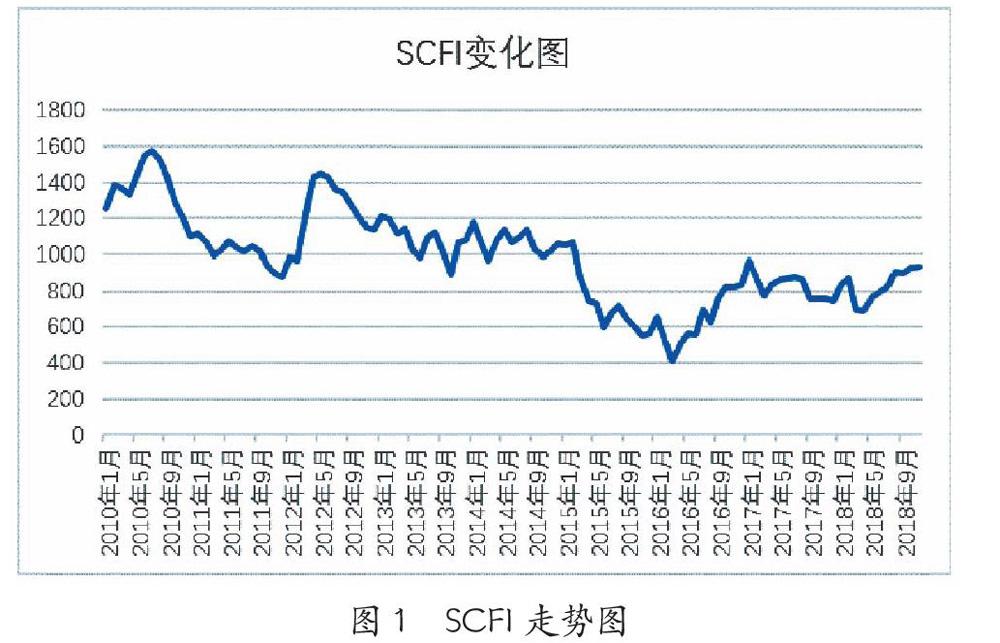
2009年10月16日，上海航運交易所推出新版上海出口集裝箱運價指數，基期為1 000點。本文對上海出口集裝箱運價指數取樣做研究，時間上從2010年1月到2018年11月，數據來源于中華人民共和國交通運輸部每月公布數據， 對這107個SCFI數據做圖，具體走勢如圖1所示。從圖1可知，SCFI指數呈不規則的鋸齒波動，最高點將近1 600點，而最低點僅僅在400點附近，整體上可以看出波動幅度不小。

3.2 SCFI序列的單位根檢驗

由圖1可以看出，SCFI序列不符合零均值同方差的特征，可以初步判斷原時間序列是不平穩的，同時結合自相關系數圖和單位根檢驗判斷，可知自相關系數沒有很快地衰減向零，不符合平穩性時間序列的特征。通過Eviews自帶單位根檢驗可知檢驗統計值t=-2.887，大于顯著性水平10%的臨界值，所以不能拒絕原假設，序列存在單位根，序列是非平穩。

由于原序列的非平穩性，所以要對SCFI序列進行一階差分，可知一階差分后序列的自相關系數一階后都顯著落在置信區間內。單位根檢驗中t統計量值是-7.648，小于顯著性水平為1%的臨界值，表明至少可以在99%的置信水平下拒絕原假設，因此可以認為差分后的序列不存在單位根，序列是平穩的。

3.3 lnSCFI序列的單位根檢驗

3.3.1 lnSCFI序列的基本統計特征（見表1）

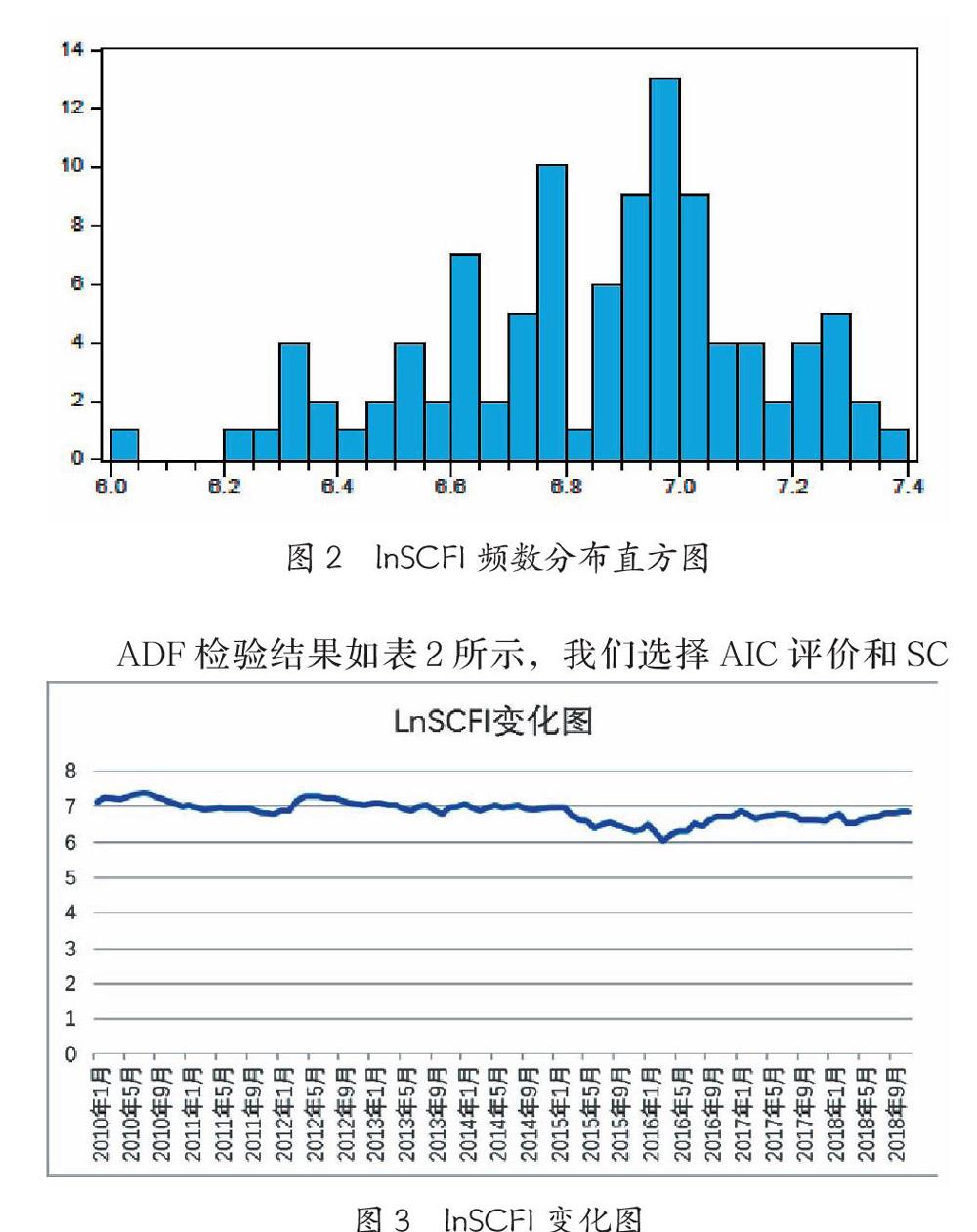
0.030725小于3，是瘦尾特征;偏度值小于0，是負偏態。J-B檢驗結果顯示的概率為0.107大于0.05， 所以認為lnSCFI序列服從正態分布。從圖2 lnSCFI的頻數分布圖中可以顯著觀察這些特征。

3.3.2 lnSCFI序列平穩性檢驗及處理

由圖3可知，檢驗序列不存在一個明顯偏離位置的隨機變動，所以看作所檢序列均值為0。但是，隨著時間的增加，被檢序列的波動趨勢變大，因此存在時間趨勢，在回歸方程中加上時間趨勢項。

ADF檢驗結果如表2所示，我們選擇AIC評價和SC評價檢驗值最小的滯后項數，檢驗值相同時，選擇滯后期最小的值，通過表3-2可知，滯后期為1時的AIC和SC最小，所以選擇滯后一期。從表2可知，ADF檢驗值為-1.660755，大于顯著水平為10%的臨界值，接受原假設，所以lnSCFI存在單位根，是非平穩的。

4 實證分析

4.1 ARIMA模型建立

4.1.1 方程的識別、定階

從一階差分后的自相關函數圖和偏自相關函數圖4中可以看到，偏自相關系數和自相關系數在一階時就都顯著落在置信區間內，使得我們難以采用傳統的自相關、偏自相關函數殘差方差圖、F檢驗、準則函數來確定模型的階數。對于這種情況，通過反復對模型進行估計比較不同模型的變量對應參數的顯著性以及AIC準則和SC準則來確定模型階數。最后確定模型為ARIMA（2，1，2），對應的所有回歸系數的顯著性水平達到99%，其它試算模型的回歸系數的顯著性水平遠不如該模型，同時該模型的AIC數值和SC數值是所有試算模型中最小的。綜合考慮選定ARIMA（2，1，2）作為上海出口集裝箱運價指數的均值預測方程。

4.1.2 模型擬合結果

由模型的系數的t統計量及其p值可知，模型所有解釋變量的參數估計值在99%的顯著性水平下都是顯著的。模型建立后，可對模型擬合殘差的效果圖觀測，觀察波動的集群現象是否減弱或消除。從的圖4模型殘差分布圖可知，序列的波動集群效應已減弱，不存在強的ARCH效應。

4.2 建立SCFI波動性的ARCH模型

4.2.1 lnSCFI的ARCH LM檢驗

為檢驗SCFI波動是否具有條件異方差，我們對ln（SCFIt）序列進行檢驗，所謂條件異方差是指預測數據與實際數據的誤差常常會成群出現，在某一時期里相對地小，而在另一時期里相對地大，誤差項的條件方差不是某個自變量的函數，而是隨著時間的變化并且依賴于過去誤差的大小。利用OLS （普通最小二乘法）進行估計得到由上面估計值可知此方程統計顯著，擬合程度也很好，但觀察其擬合方程的殘差序列圖5可看到有波動成群現象，這意味著序列ln（SCFIt）可能具有條件異方差性，所以上式進行ARCH LM檢驗。

得到的檢驗結果： 一階ARCH效應的相伴概率為0.0036，小于0.05，拒絕原假設。說明殘差序列存在ARCH效應，但不存在高階ARCH效應。因此采用ARCH模型對式ln（SCFIt）=0.936849ln（SCFIt-1）+ut的隨機擾動項建模以充分提取殘差中的信息，使最終的模型殘差成為白噪聲。

4.2.2 模型結果

首先變量ln（SCFIt-1）的系數估計值近似為1，表明是單位根過程。然后，方差方程中ARCH項的系數為0.253<1，滿足約束條件且P值為0.0447<0.05是統計顯著的，Log likelihood對數似然值變大，AIC、SC變小，都證明ARCH（1，1）模型可以更好地擬合ln（SCFIt），反映lnSCFI的波動。

4.3 ARIMA模型預測結果

用擬合的有效模型ARIMA（2，1，2）的預測值與部分實際值對比得知模型的預測精度可行。并進行短期預測，得出2018年12月至2019年3月的預測值見表4-1。

根據預測結果顯示上海出口集裝箱運價指數將在未來5個月中有波動小幅度上漲，總體圍繞925點上下波動，市場趨于穩定，與實際指數在2019年3月有較大偏差，說明模型對于短期的末期的描述并不充分，需要考慮其他影響因素的誤差修正。

5 結論與展望

5.1 結論

通過使用計量經濟學方法和Eviews軟件操作，得出ARIMA（2，1，2）模型對上海出口集裝箱運價指數時間序列的擬合效果較好，進行短期預測能有較高的預測精度，在不發生較大經濟危機或突發事態的情況下，上海出口集裝箱運輸運價市場走向將在未來4個月中有波動小幅度上漲，總體圍繞925點上下波動，接近基期1 000點的水平，相較于市場谷底來說，已經是大幅度回暖了。針對SCFI的波動性，對SCFI的對數序列進行分析和檢驗，最終得出ln（SCFIt）的一階差分序列平穩，并且通過ARCH LM檢驗法對ln（SCFIt）誤差項進行檢驗，結果表明具有一階條件異方差性。這說明SCFI容易受到外界影響的干擾，比如經濟發展情況，國際貿易情況以及行業相關政策的影響。使用ARCH （1，1） 可有效消除條件異方差，更好地擬合了SCFI的波動，有助于研究開發出針對上海出口集裝箱運價的運費衍生品，為相關港航企業提供定價參考，為政府部門的決策調控提供幫助，助力上海國際航運中心的建設。

5.2 未來研究展望

由于模型自身和數據收集的局限性，只從時間序列本身的特性考慮，而沒有考慮其他不確定因素的影響。雖然模型中是以隨機項來反映這些不確定因素，但在預測期望值中其他不確定因素的影響是無法反映出來的。未來研究可以收集相關不確定因素的數據，來建立向量誤差修正（VECM）模型對短期波動進行修正，使得模型的短期預測的效果更加良好。受到數據收集的限制，本文只采用了月度數據進行研究分析，未來研究可以使用周度數據來進行更加精確的分析，使得短期波動的狀況更加貼合實際。

參考文獻

[1] Cullinance K. A short-term adoptive forecasting model for BIFFEX speculation; a boxjenkins approach. Maritime Policy&Management.1992，2：91-114.

[2] Kavussanos M G， Alizadeh-M A H. Seasonality patterns in dry bulk shipping spot and time charter freight rates[J]. Transportation Research Part E： Logistics and Transportation Review， 2001， 37（6）： 443 -467.

[3] BERG-ANDREA SSEN JA. Some Properties of international maritime statistics[J].Mritime Policy&Management1996.（4）.381-395.

[4] George E.P.Box， Gwilym M. Jenkins， Gregory C. Reinsel.時間序列分析-預測與控制（原書第四版）[M].上海：機械工止出版社.2011.

[5] 陶長琪.計量經濟學教程[M]上海：復旦大學出版社， 2012.

[6] 高鐵梅.計量經濟分析方法與建模：Eviews應用與實例（第二版）[M].北京：清華大學出版社，2006.

[7] 陳昭，劉巍，歐陽秋珍.計量經濟學軟件Eviews9.0簡明操作教程[M].北京：中國人民大學出版社，2017.

[8] 趙國慶.經濟分析中的時間序列模型[M].天津：南開大學出版社.2012.

[9] 蔣迪娜.我國出口集裝箱運價指數研究[J].山西財經大學學報，2005，27（5）：90-94.

[10] 張小斐，田金方.基于ARIMA模型的短時序預測模型研究與應用[J].統計教育，2006，（10）：7-9.

[11] 朱玉華，趙剛.基于ARCH族模型的中國出口集裝箱運價指數波動特征[J].上海海事大學學報，2013，（3）：48-52.

[12] 安瀟瀟.ARMA相關模型及其應用[D].哈爾濱.燕山大學.2008.

[13] 賀強.基于GARCH模型的國際干散貨運價指數波動性研究[D].大連.大連海事大學，2013.

[14] 原云霄，王寶海.基于ARIMA模型對我國公路物流運價指數的預測[J].數學的實踐與認知，2017，（23）：53-56.

[15] 李耀鼎，宗蓓華.波羅的海運價指數波動研究[J].上海海事大學學報，2007，27（4）：84-87.