平板陣列隔熱瓦幾何參數的分析與優化

汪艷秋，王志瑾，葉 紅

（南京航空航天大學 飛行器先進設計技術重點學科實驗室，南京 210016）

0 引言

高超聲速飛行器在再入大氣層的過程中，由于與表面氣體的摩擦會產生很大的熱量，導致飛行器表面溫度急速升高。為了確保飛行器的安全，采用熱防護結構是非常必要的。陶瓷隔熱瓦是應用于高超聲速飛行器的一種可重復使用的熱防護系統，一般由剛性陶瓷隔熱瓦、應變隔離墊與機身蒙皮通過膠體連接。由于隔熱瓦材料具有易碎的特性，導致隔熱瓦承熱不承力，而蒙皮承力不承熱，故在隔熱瓦和蒙皮中間須使用應變隔離墊進行變形協調；另外，隔熱瓦材料受熱會膨脹，故瓦塊之間必須留有足夠的縫隙，以避免相鄰瓦塊擠壓破裂。陶瓷隔熱瓦以陣列的形式敷設于機體表面，瓦間縫隙既可給單塊隔熱瓦的熱膨脹變形預留空間，也可協調隔熱瓦間的受載變形。

文獻[1]從流、熱、固3個方面對隔熱瓦組件進行分析與設計，得到隔熱瓦組件的縫隙參數對縫隙熱流分布的影響規律，認為縫隙寬度是影響縫隙內部熱環境的關鍵因素。文獻[2]對陶瓷隔熱瓦采用二維有限元模型進行熱力耦合分析，并對模型進行優化，最后利用優化模型得到隔熱瓦之間縫隙寬度的范圍。文獻[3-5]針對隔熱瓦的厚度或者縫隙寬度進行研究，但均未對縫隙間距的影響進行分析，也未采用三維模型對縫隙參數進行詳細研究。

本文采用三維隔熱瓦陣列有限元模型，分析在瞬態氣動熱載荷和氣動力載荷同時作用下，隔熱瓦的縫隙寬度和縫隙間距等幾何參數對隔熱瓦熱變形的影響，并據此對隔熱瓦陣列進行優化設計。

1 平板陣列隔熱瓦系統

陶瓷隔熱瓦熱防護系統如圖1所示，隔熱瓦通過膠體粘貼在應變隔離墊上，瓦塊之間留有縫隙，應變隔離墊通過室內固化膠與蒙皮黏合。

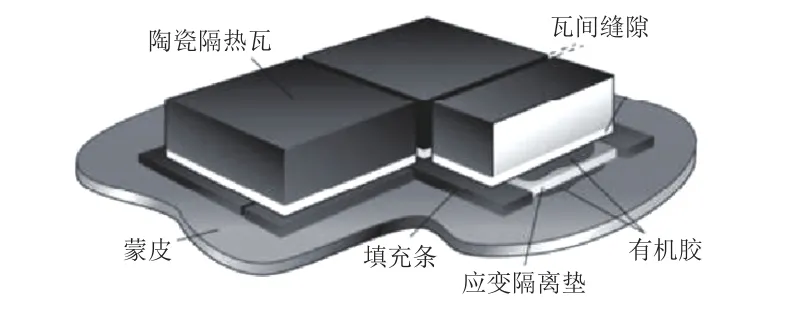
圖1 陶瓷隔熱瓦防護系統Fig.1 Composition of a ceramic thermal insulation tile

1.1 陣列布局

正方形隔熱瓦的陣列布局如圖2所示：單片瓦塊邊長為L；每一行中相鄰瓦塊的間隙定義為縫隙寬度a；行與行之間的瓦塊縫隙可錯位布置，其錯位距離定義為縫隙間距b。a、b統稱為縫隙參數。

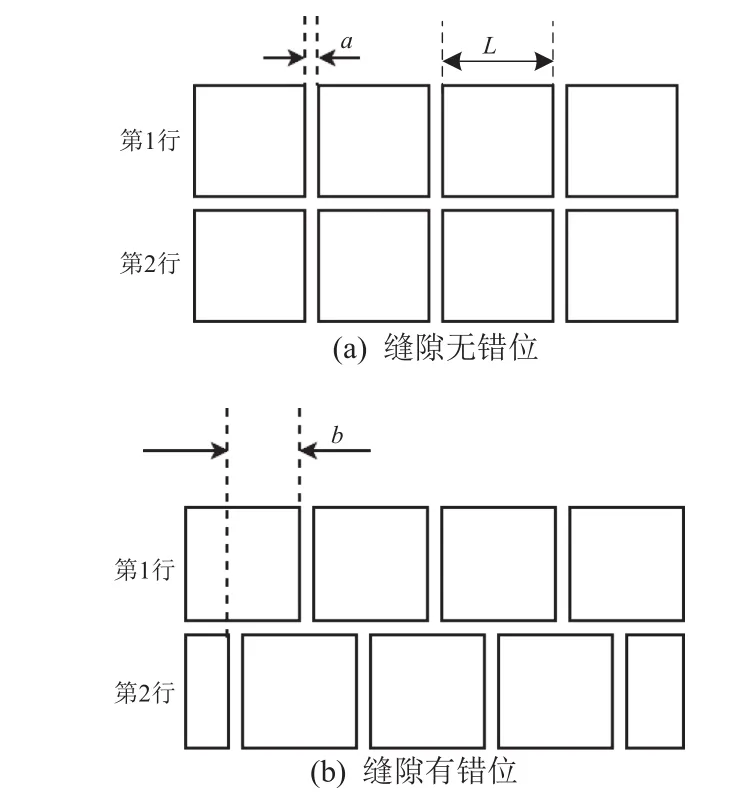
圖2 隔熱瓦陣列布局示意Fig.2 Layout of the array insulation tile

1.2 熱分析方程

在給定的再入初始溫度（隔熱瓦、應變隔離墊、蒙皮整體的溫度）下，將熱流載荷加載在熱防護系統表面，模擬飛行器再入過程中隔熱瓦的溫度變化歷程，進行熱響應分析。

傳熱現象的本質是由于溫度差引起的熱能轉移，對于熱防護系統來說，傳熱方式包括熱傳導、對流傳熱和輻射散熱，本文僅考慮熱傳導和熱輻射。瞬態傳熱的過程中，系統內節點的溫度、熱流密度、熱邊界條件和系統的內能都隨著時間出現顯著的變化，而隔熱材料的熱物理性能隨著溫度變化，因此熱分析方程是非線性的[6]。非線性熱分析的熱平衡方程可以矩陣的形式表述為CT+KT=Q，其中：C為比熱容矩陣；T為節點溫度矢量；K為結構熱傳導矩陣；Q為節點熱流密度矩陣。

2 分析算例

2.1 分析對象

在面積為 1000 mm×1000 mm 的正方形區域，給定初始尺寸參數：隔熱瓦邊長L=150 mm，厚度H=50 mm，縫隙寬度a=0.3 mm，縫隙間距b=45 mm；蒙皮為鋁合金，厚度為2.5 mm；應變隔離墊厚度為2 mm。

2.2 模型簡化

對模型進行合理的簡化，忽略極薄膠層的熱阻，只考慮隔熱瓦、應變隔離墊和蒙皮；并為降低問題復雜度，采用近似處理方法，忽略結構尺寸對環境的影響，不考慮隔熱瓦的縫隙大小對局部外熱流的影響[7]，重點研究縫隙寬度和縫隙間距對隔熱瓦組件的變形及瓦間接觸應力的影響。

2.3 模型材料

該熱防護組件中，隔熱材料選用剛性陶瓷隔熱瓦，金屬蒙皮采用鋁合金。考慮材料熱物理性能的非線性，隔熱瓦組件的材料屬性如表1～表3所示。

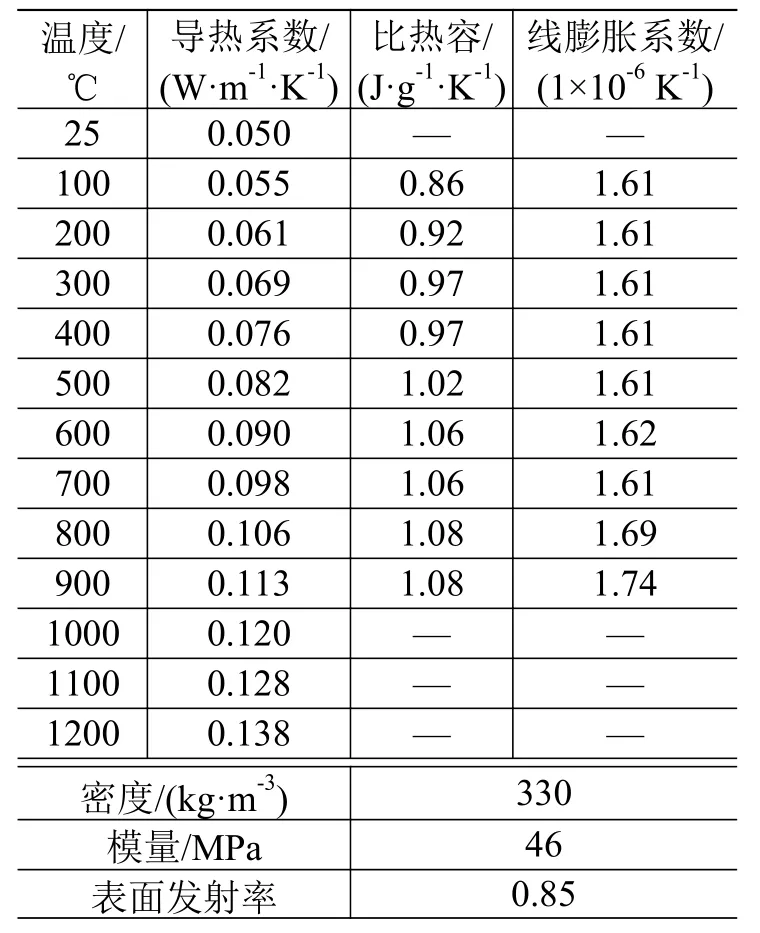
表1 剛性隔熱瓦熱物性參數Table 1 Thermal-physical parameters of rigid thermal insulation tile

表2 應變隔離墊熱物性參數Table 2 Thermal physical parameters of strain-isolating pad

表3 鋁合金熱物性參數Table 3 Thermal physical properties of aluminum alloy

2.4 加載條件

工程項目部門給定的再入過程的熱流密度載荷如圖3所示，總的再入時間為1600 s，熱流密度曲線變化主要分為3段：從再入初始到500 s以前是上升段，熱流密度隨著時間的延長逐漸增大；在500 s左右熱流密度達到最大值，并持續約 1000 s；隨后熱流密度逐漸降低，直到著陸。在每塊隔熱瓦的上表面同時模擬施加再入過程熱流載荷和均布氣動力載荷0.06 MPa（此數值由工程項目部門給定），考察熱流和氣動力共同作用下的隔熱瓦組件整體變形。

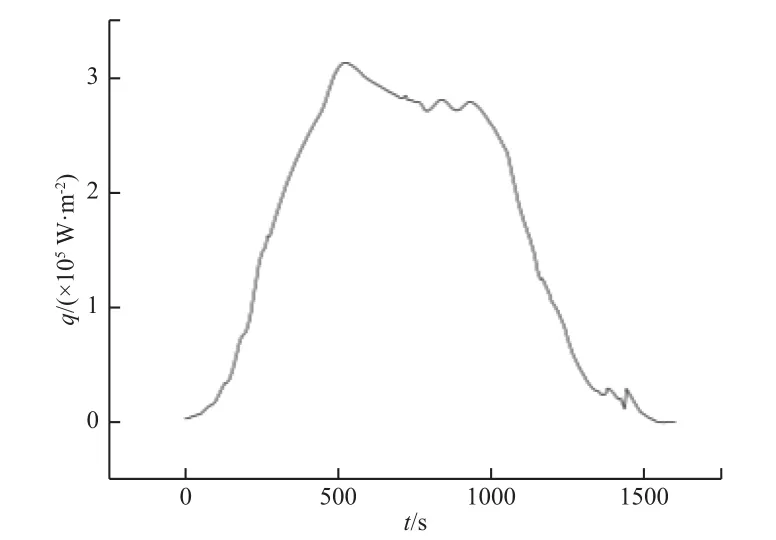
圖3 熱流密度隨再入時間變化曲線Fig.3 Heat flux versus re-entry time

2.5 邊界條件

1）熱分析邊界條件：整個組件初始溫度場溫度為298 K；每塊隔熱瓦上表面施加熱載荷，環境溫度為298 K，隔熱瓦表面發射率為0.85。

2）力分析邊界條件：單位面積的鋁蒙皮四周固支；隔熱瓦的側面及上表面為自由邊界，下表面與應變隔離墊黏結在一起。

2.6 初步計算結果及分析

如圖4所示，隔熱瓦組件中心位置的鋁蒙皮發生下凹，變形最為嚴重；面板凹陷使隔熱瓦向中間擠壓，造成隔熱瓦之間距離變小（圖5），越靠近外表面的瓦間距離越小，導致相鄰瓦塊相互擠壓，出現瓦間接觸應力（圖6）。接觸力會造成瓦塊破裂，損壞熱防護系統。

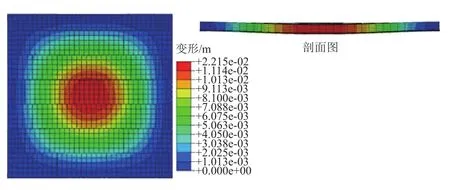
圖4 隔熱瓦組件整體沿厚度方向變形分布Fig.4 Deformation of tiles along thickness direction

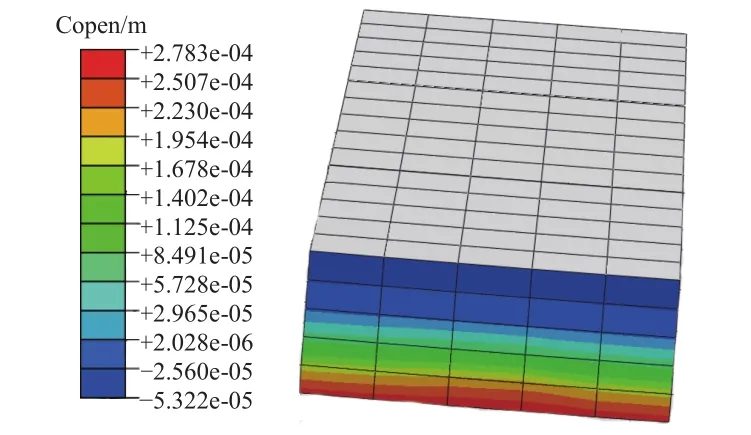
圖5 瓦間距離Fig.5 Distance of tiles

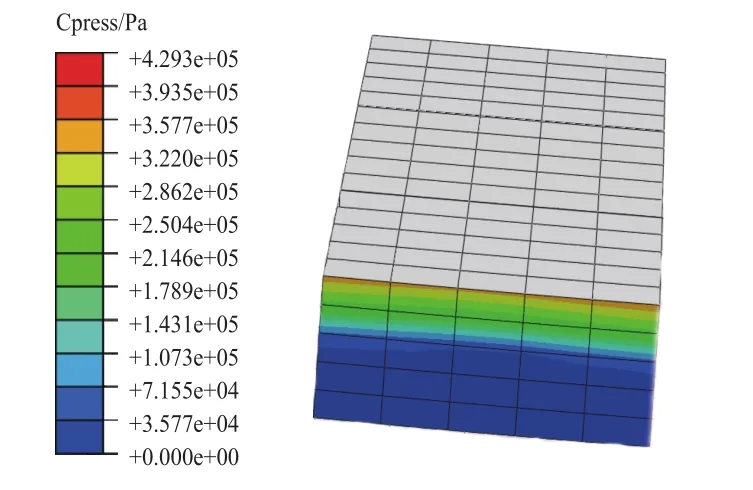
圖6 瓦間接觸應力Fig.6 Contact stress between tiles

3 構建接觸應力優化模型

在上述研究的基礎上，依據設計條件，對結構縫隙參數進行優化。隔熱瓦參數分析及優化設計流程如圖7所示。

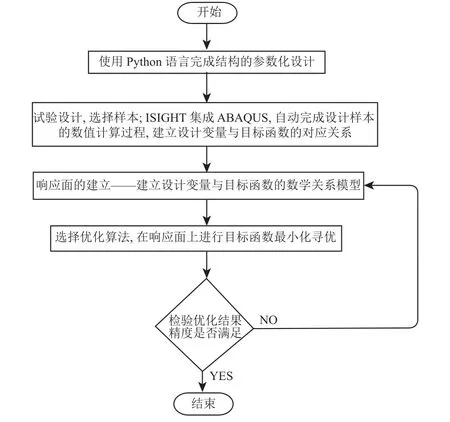
圖7 隔熱瓦參數分析及優化設計流程Fig.7 Flowchart for parameter analysis and optimization design of tiles

擬考慮12種幾何參數（見表4）的隔熱瓦，若利用ABAQUS對每種隔熱瓦組件都進行前處理、計算分析和后處理，其工作量及耗費時間都將非常大。因此運用Python語言編制個性化程序，實現了隔熱瓦前處理、分析計算和后處理的參數化，只需手動修改參數就可由軟件自動完成隔熱瓦組件的建模、劃分網格、提交計算及數據后處理等工作，提高了設計效率[8]。設計對象為平板陣列隔熱瓦的縫隙參數，利用試驗設計法選取樣本點，計算不同縫隙參數下的隔熱瓦間最大接觸應力；然后根據計算結果，用響應面法建立近似模型，并對其進行誤差分析；最后使用ISIGHT自帶優化算法對近似模型進行優化分析，并利用有限元軟件進行優化結果驗證。

表4 隔熱瓦幾何參數組合Table 4 Geometric parameter combinations

4 平板陣列隔熱瓦優化設計

4.1 優化方式及設計變量

固定L=100 mm、H=40 mm，通過改變隔熱瓦縫隙寬度a和縫隙間隔b來進行縫隙參數的采樣，計算后擬合近似模型。該方法將有限元模型擬合成無限近似的數學模型，提高了求解效率。

4.2 近似模型

為了提高近似數學模型的精度，本文根據二次響應面法所需要的最低樣本點數量，用最優拉丁超立方設計法[9]采樣選取30組樣本點。該方法與普通的正交采樣相比精確度較高，且選取樣本點可遍及整個采樣空間（參見圖8）。具體采樣范圍如表5所示。

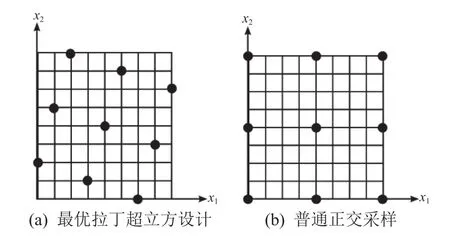
圖8 最優拉丁超立方設計與普通正交采樣對比Fig.8 Optimal Latin hypercube design vs.quadrature sampling

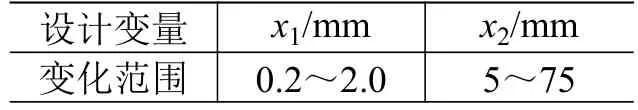
表5 設計變量的變化范圍Table 5 Range of the design variables

令縫隙寬度為變量x1、縫隙間距為變量x2，完成30組x1和x2采樣數據后，利用ISIGHT的二次響應面法建立最大接觸應力與縫隙寬度、縫隙間距的近似模型，即最大接觸應力y=f(x1，x2)，其二元二次回歸模型為。

Pareto圖（圖9）反映變量對結果的影響程度，藍色表示正效應，紅色表示反效應。由圖可見：縫隙寬度和縫隙間距對最大接觸應力是反效應，即縫隙寬度和縫隙間距越大，最大接觸應力越小，這也與二元二次回歸模型表達式中相應變量前的系數符號相對應。交互效應圖（圖10）中縫隙寬度與縫隙間距2條曲線不平行，表明它們之間有交互作用。相關性圖（圖11）則顯示了輸入參數（縫隙寬度、縫隙間距）對輸出參數（最大接觸應力）的相關性。主效應圖（圖12）顯示縫隙寬度對接觸應的影響所占比重較大，因此在后續優化中，縫隙寬度的權重較大，同時也需考慮縫隙間距的影響。

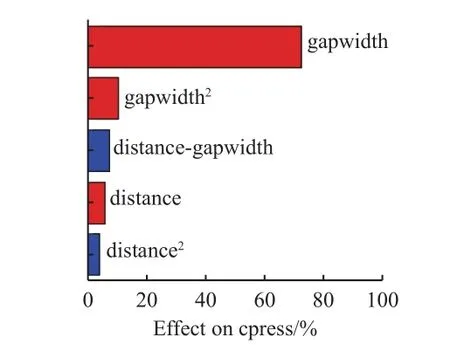
圖9 瓦片縫隙參數的 Pareto 圖Fig.9 Pareto diagram of tile gap parameters

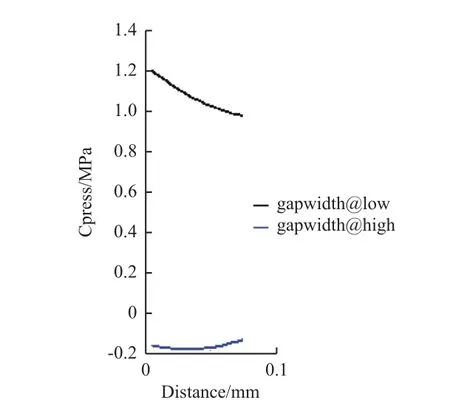
圖10 瓦片縫隙參數交互效應圖Fig.10 Interactive effect of tile gap parameters

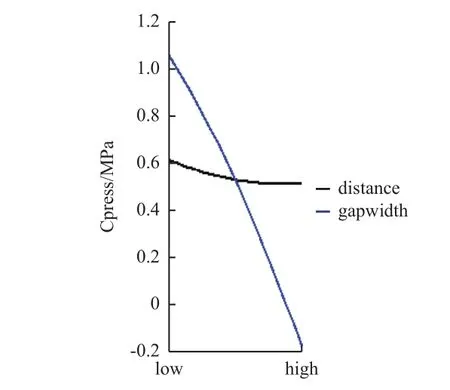
圖11 瓦片縫隙參數相關性圖Fig.11 Correlation graph of tile gap parameters

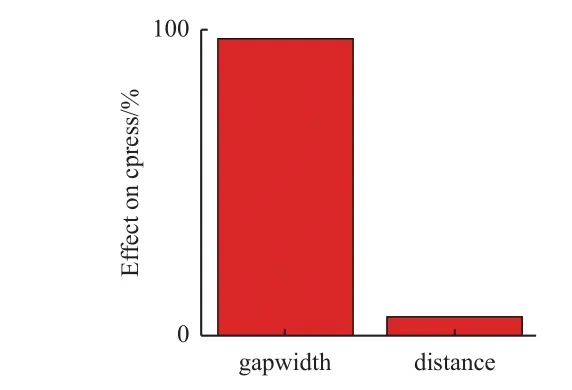
圖12 瓦片縫隙參數主效應圖Fig.12 Principal effect of tile gap parameters

4.3 誤差分析

采用10個樣本點以及計算值進行分析，結果R2=0.980 09，接近于 1，說明誤差較小。

4.4 平板陣列隔熱瓦縫隙參數優化結果

得到回歸模型之后，利用ISIGHT軟件進行優化設計，尋找最大接觸應力y最小時對應的縫隙寬度x1和縫隙間距x2，其計算流程如圖13所示。最終，L=100 mm、H=40 mm 的平板陣列隔熱瓦縫隙參數的優化結果為：縫隙寬度1.7 mm、縫隙間距50 mm。

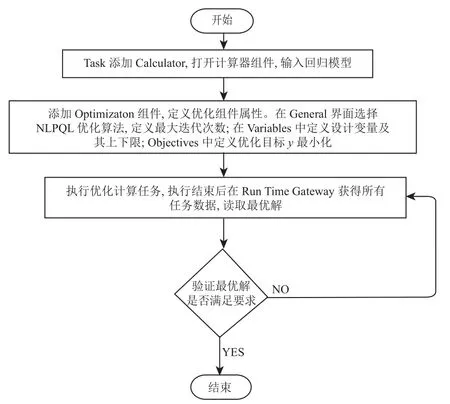
圖13 參數優化迭代算法流程Fig.13 Flowchart of iterative algorithm

4.5 優化結果驗證

將優化得到的縫隙寬度1.7 mm、縫隙間距50 mm代入對應隔熱瓦組件的有限元模型進行分析計算，結果顯示未產生接觸應力，說明優化結果合理。因不具備實驗驗證條件，本文僅進行了有限元仿真分析驗證。

4.6 其余幾何參數隔熱瓦組件的優化結果

針對不同的隔熱瓦幾何參數組合，得出如表6所示的優化設計結果，可以看出：同種厚度下，隔熱瓦邊長越大，所需要的縫隙寬度越大；同種隔熱瓦邊長下，隔熱瓦厚度越大，所需要的縫隙寬度越大；縫隙間距在數值上約可取為隔熱瓦長度的1/2。

表6 隔熱瓦幾何參數優化結果Table 6 Optimization result of the tile gap parameters

5 結論

在外部熱流相同且僅考慮隔熱瓦縫隙寬度和縫隙間距這2個參數的情況下，根據本文計算和分析結果得到以下結論：

1）縫隙寬度是影響隔熱瓦間接觸應力的主要因素，縫隙寬度越大則縫隙間的接觸應力越小，但是進入隔熱瓦組件底部的熱流越多。因此，考慮到蒙皮所能承受的溫度上限，在隔熱瓦接觸應力最小的前提下縫隙的寬度越小越好。

2）縫隙寬度和縫隙間距均會影響隔熱瓦的變形，但由縫隙間距帶來的影響微乎其微。因此，進行隔熱瓦組件幾何參數優化時主要考慮縫隙寬度的影響；將縫隙間距設為隔熱瓦長度的1/2，即令隔熱瓦間的縫隙與其相鄰行隔熱瓦的中線對齊即可。

3）隔熱瓦厚度也會對縫隙寬度的確定帶來影響，隔熱瓦越厚，隔熱瓦組件整體變形時，隔熱瓦的上部越容易相互接觸，為了不產生接觸應力所需要的縫隙寬度就越大。