淺析輔助線在高中數學幾何題中的重要作用

鄒文韜

(湖南師大二附中 410000)

最為一名高中生在學習數學幾何過程中經常會出現無從下手的現象，因此在解題時我們需要對其中的已知條件進行詳細閱讀，避免陷入出題者設計的陷阱.而在高中幾何解題過程中使用輔助線具有重要幫助，有效降低幾何題的難度，縮短解題時間，同時還可以提高解題的準確性.

一、高中數學幾何學習的難點

高中數學幾何題具有難度相對較大的特點，其中還會涉及到計算和證明內容，并且出題者一般會將其他數學知識與幾何知識相結合提高題目的難度.我們在解答幾何題時感覺比較困難主要表現為以下幾點：首先，空間立體思維相對較差，在高中幾何解題中需要我們具有超強的邏輯思維能力，但幾何題經常會給人一種抽象的感覺，很難在頭腦中形成立體畫面；其次，在解題過程中很難找到正確的解題思路，看到問題后經常會表現得無所適從，不知該用哪種方式證明；第三，解題方案相對較少，我們在解題過程中經常會出現邏輯思維混亂現象，無法做到舉一反三，而且在添加輔助線時也不知道該在什么地方加；最后，對問題分析不足，在解題時對問題的分析不足，從而無法掌握解題條件，因此在解題中經常會出現繪制輔助線錯誤現象，從而影響解題效果.

二、輔助線在高中數學幾何解題中的重要性

1.能夠將復雜的幾何題簡單化

輔助線在解決高中幾何問題中比較常見，出題者在出題的過程中經常會將問題復雜化，從而增加問題的復雜難度，因此我們經常會利用輔助線，將復雜的問題進一步簡單化，從而便于理解題目.在解題過程中我們需要合理地應用輔助線，讓思路變得更加清晰，有效降低幾何問題的難度.

例1在三棱柱ABC-A1B1C1中，其底部的A1B1C1為等腰三角形，已知底部∠ABC=90°，同時還知道AA1=AC，并且點D為線段CC1的中點，那么二面角B-B1D-A的大小為多少？

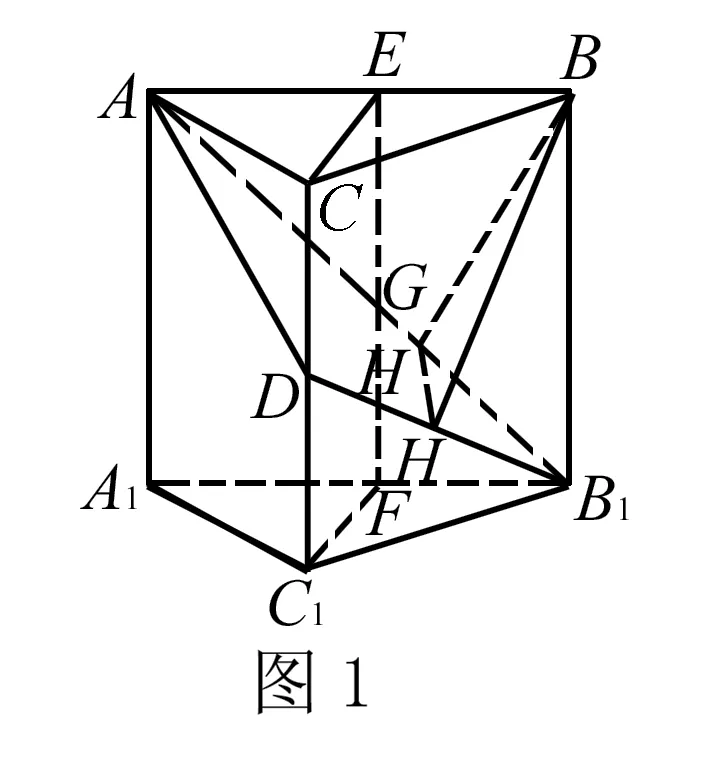
解決以上問題，在思索的過程中會感覺非常復雜，那么首先我們需要畫出題目中所給出的條件，如圖1.與此同時分析所提出的問題，在解題時直觀地計算二面角B-B1D-A的大小非常困難，所以需要引入輔助線.添加輔助線時我們找到AB中點和A1B1的中點引入輔助線EF和CF，緊接著我們還需要作出CC1和EF中點的連線，也就是DG，并連接AB1和DB1，具體輔助線如圖1.因此在解題中采用垂面，作出其中的垂線進行解題，并畫出其中的點H，以此來確定其中的二面角，最后再對問題進行分析就會顯得比較簡單.

2.能夠體現出隱含的已知條件

在高中幾何解題中經常會出現隱含條件現象，從而增加解題難度，因此在平時練習幾何解題時，需要對已知條件進行全面了解和分析，充分挖掘其中的隱藏條件，并適當添加輔助線，降低幾何題目的難度.

例2 已知空間四邊形ABCD，其中的AD與BD相等，AC與BC相等，并且點E為AB的中點.證明平面CED與直線AB垂直.

在解題過程中，先畫出問題中已知的條件，從而呈現出題目中所給出的條件，讓整個解題思路變得更加清晰(如圖2).在證明以上問題中所提到的平面CED與直線AB相垂直過程中，需要合理應用等腰三角形三線合一的性質，因此在解題時首先應該求證直線AB同時垂直于DE和EC，然后再證明一條直線垂直于兩條相交的直線，那么該直線就垂直于這兩條直線共同所在的平面，最后得出平面CED與直線AB相垂直.根據對以上案例進行分析，可以得出在幾何解題中充分應用輔助線對解題有重要幫助，不但能夠將抽象的空間問題變得更加直觀化，同時對縮短解題時間有重要幫助.

3.將原圖形進行變化

在解題過程中將原圖形進行平移、旋轉等從而得到所需的圖形，顯露出各線段以及角度之間的關系.

例3已知四邊形ABCD，其中AB與CD相等，并且其中點E、F分別為BC和AD的中點，其中BA、EF和CD分別相交，最終形成∠α和∠β，如圖3所示.求證∠α=∠β.

在此過程中我們需要引入輔助線，并將其中部分圖形進行平移，把∠α和∠β的頂點集中到一個已知點上，同時還需要將直線AB與CD進行平移，因此可以作出以下輔助線，過點F作出FG平行并且等于AB，作FH平行且等于CD，然后將EG、EH、BG以及HC相連接.為了證明∠α=∠β，只需要證明∠1=∠2即可.由于條件可知AB與FG、BG與AF以及FH與DC平行且相等，從而得出△FHG為等腰三角形，并且因為FE是△FGH底邊的中線，因此可以推出FE為∠GFH的平分線，因此可得∠1=∠2，由此可得∠α=∠β.

綜上所述，高中數學幾何題具有空間感強、邏輯思維強的特點，我們在學習和解題過程中不僅難度相對較大，同時解題的準確率也相對較低.經過對上文分析可得，在高中幾何解題中適當添加輔助線可將復雜的問題簡單化，從而便于我們在解題時能夠清楚地了解其中的已知條件，因此輔助線在高中數學幾何解題中的重要作用研究，能夠有效提高我們的解題質量.