大型風力機變槳系統前饋反饋復合控制仿真研究

任海軍， 張 浩， 馮明馳

(重慶郵電大學 先進制造工程學院， 重慶 400065)

0 引 言

風速超過額定值后，風力機輸出功率需要保持恒定，變槳距方式是調節風力機輸出功率的主要方式之一[1-5]。通過改變變槳角度，使葉片攻角發生變化，作用在葉片上的推力隨之改變，從而達到調節輸出功率的目的。

為了使得槳距角能夠按照給定目標作調整，需要有效的控制算法。PID控制器由于結構簡單、易于實現、可靠性高等特點受到廣泛應用，但其比例、積分、微分系數不易調整。因此通常將模糊控制、神經網絡、遺傳算法等與PID控制器相結合，提高控制器的性能[6-9]。也可以直接采用智能控制算法直接對變槳角度進行控制。這些控制算法通常是反饋控制的形式，當控制偏差出現后，反饋控制器才產生作用。而且，由于大型風力機葉片長、質量大，變槳過程呈時間滯后現象，反饋控制進一步加劇了時滯的影響。

前饋控制是一種超前控制方法，通過提前置入控制量，補償系統時滯，提高系統的控制性能[10-11]。在風力機系統中，根據風速預測值提前調節變槳角度，補償由系統滯后引起的控制滯后。

本文通過Simulink建立風力機系統模型，建立風速和槳距角映射關系，設計前饋反饋復合控制器，并用粒子群算法優化PID控制器參數。采用這種可視化軟件使理論知識直觀化的方法，可以使學生了解到狀態變量的動態變化過程，更容易理解抽象知識。而且，理論與實踐相結合的方式可以激發學生的學習積極性和主動性，提高教學效果。

1 風力機系統模型

1.1 空氣動力學模型

風推動風輪旋轉，經過增速系統，將較低的旋轉速度轉換為較高轉速，帶動發電機工作。風速、風輪直徑等是影響輸出功率的主要因素，但當風力機確定以后，這些因素不受人為控制。另外一個對輸出功率產生重要影響的因素是能量轉換系數，它受葉片的氣動力影響，同時，可以采用一定的方式對此系數進行控制。風力機輸出功率為[1]:

(1)

0.001 84(λ-3)β

(2)

λ=ωrR/V

(3)

式中:Pa為風力機輸出軸功率;ρ為空氣密度;R為風輪半徑;Cp為能量轉換系數;λ為葉尖速比;β為變槳角度;V為風速;ωr為風輪轉速。

1.2 傳動系統模型

傳動系統是風力機系統中的重要組成部分，有柔性傳動鏈和剛性傳動鏈之分。為了簡化模型，并不失模型的一般性，在此將傳動鏈考慮為剛性結構，其動態特性表達式為[1]：

(4)

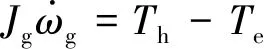
(5)

Tz=bωr

(6)

(7)

式中:Jr為風輪轉動慣量;Ta為風力機氣動轉矩;Tz為阻力距(假定阻力距主要集中在齒輪箱的低速端);Tl為齒輪箱低速端轉矩;Jg為發電機轉子轉動慣量;ωg為發電機轉子轉速;Th為齒輪箱高速端轉矩;Te為發電機電磁轉矩;b為阻力距常數;k為齒輪箱傳動比。

將式(5)、(6)、(7)代入式(4)，可得：

(8)

式中，Jz=k2Jg+Jr。

2 風力機變槳系統前饋反饋仿真模型

風速超過額定值后，需要使輸出功率恒定不變。本文采用變槳的方式調節風力機輸出功率，但是，變槳系統存在明顯的時滯。因此，采用前饋反饋的方式對系統進行控制，前饋控制提前置入控制量，補償變槳時滯和反饋控制時滯；當偏差出現后，反饋控制及時產生作用，消除偏差，實現目標值跟蹤控制。

卡爾曼濾波器具有濾波、狀態估計等功能。牛頓拉夫遜算法是一種迭代求解算，常用于計算機的求解過程。由于不易直接測量到風輪上風速精確值，根據電磁轉矩和風輪轉速，本文采用卡爾曼濾波器對氣動轉矩進行估計，再采用牛頓拉夫遜算法進行計算，通過迭代的方式求解有效風速估計值。由于電磁轉矩和風輪轉速容易測量，據此得到的風速準確性高且有效。在變槳控制中，常將變槳角度作為控制量，因此，采用最小二乘法建立風速和變槳角度的映射關系，再根據最優估計風速預置作為前饋控制量的變槳角度。

反饋控制環中，采用PID控制器作為控制單元。但是，PID控制器的性能與比例、積分、微分系數密切相關，而其參數調節是難點問題之一。因此，常采用智能算法對3個參數進行尋優。由于粒子群算法具有容易實現、收斂速度快、精度高等特點被廣泛應用于參數尋優、路徑規劃等領域。基于此，本文采用粒子群算法優化PID控制器參數，提高控制器性能。系統控制框圖用圖1表示。

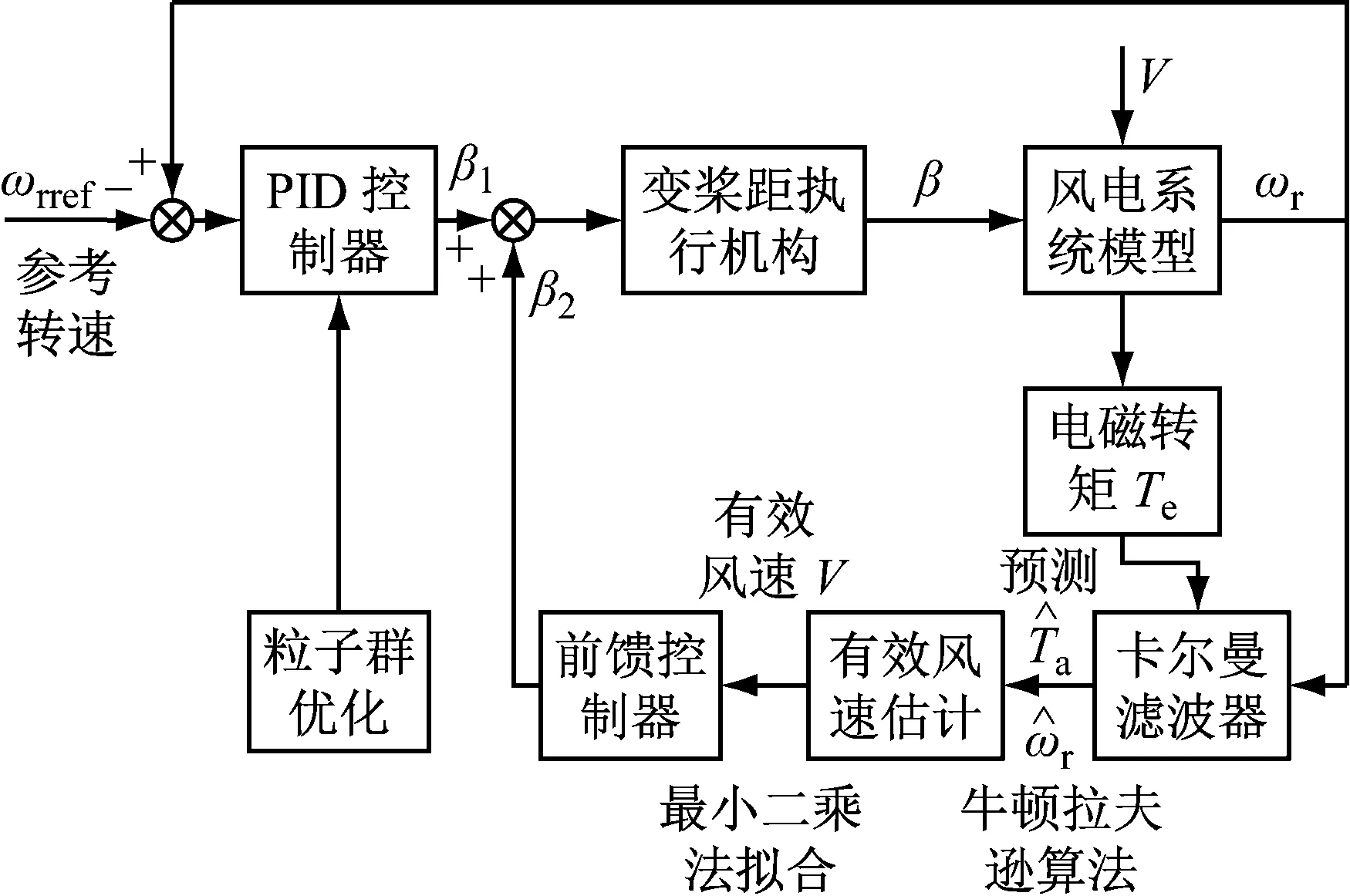
圖1 系統控制框圖

2.1 氣動轉矩估計模型

由于直接測量得到的風速不能準確表示風輪上的有效風速，因此，根據氣動轉矩對風速進行估計。但是，氣動轉矩也不易直接得到，而電磁轉矩和風輪轉速是容易直接測量的值。因此，本文根據測量得到的電磁轉矩和風輪轉速，采用卡爾曼濾波器對氣動轉矩進行估計。卡爾曼濾波器是一種經典的狀態估計方法，通過上一時刻的最優估計值和現在時刻的觀測值對下一時刻值進行估計。與此同時，對卡爾曼系數和狀態觀測矩陣進行迭代運算，可以得到每一時刻的最優值。為求氣動轉矩，首先得到其一階馬爾科夫方程式[12]:

(9)

式中:Tψ為時間常數;ε為高斯白噪聲。

將式(9)代入(8)，傳動系統的狀態方程可表示為[2]：

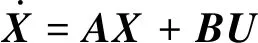
(10)

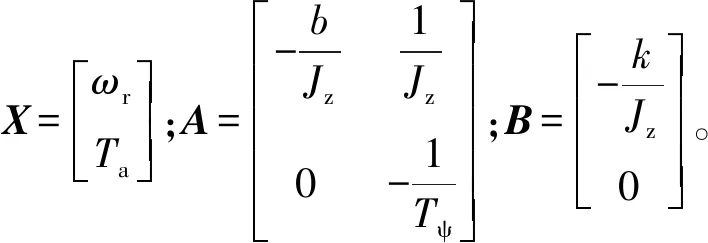
輸出方程為[2]：

Y=HX

(11)

式中，H=[1 0]

在實際應用中，為利于計算機運算，需要將連續系統轉換為離散系統。因此，對狀態方程和輸出方程進行離散化，將采樣周期設定為1 ms。在實際系統中，往往存在過程噪聲和測量噪聲，因此，在離散化過程中一并考慮。離散方程為[2]：

X(k+1)=>F(k+1,k)X(k)+

B(k+1,k)U(k)+ω(k)

(12)

Z(k+1)=H(k+1)X(k+1)+υ(k)

(13)

式中:k為當前時刻，k+1為下一時刻，X(k)為系統狀態向量，F(k+1,k)為系統狀態轉移矩陣，B(k+1,k)為控制矩陣，U(k)為控制輸入，ω(k)為過程噪聲，Z(k+1)為系統觀測值，H(k+1)為狀態觀測矩陣，υ(k)為觀測噪聲。

2.2 有效風速估計

以氣動轉矩估算風速，可以減少風速計的使用，而且，得到的風速是風輪掃掠面上的有效風速，因此，具有很高的準確性。為得到有效風速，首先建立氣動轉矩和有效風速之間的關系。最優風速的表達式為:

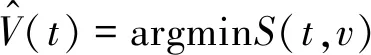
(14)

(15)

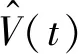
此處，優化目標函數為:

J(v)=Ta

(16)

由于風速在不斷變化，常采用迭代運算的方式計算實時風速，以此提高風速精確性。根據牛頓拉夫遜算法，有效風速的迭代過程為:

(17)

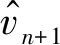
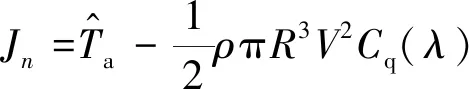
(18)

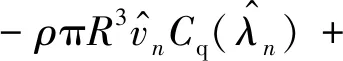
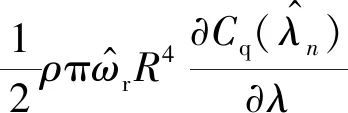
(19)

式中，Cq=Cp/λ。

2.3 風速與變槳角度映射關系

前饋控制中，置入合適的前饋控制量是實現補償的關鍵之一。在得到最優的有效風速后，如何選擇前饋變量十分重要。由于超過額定風速值后，通過調節變槳角度控制輸出功率，因此，選擇變槳角度作為前饋控制量。

對于變槳變速風力機，當達到額定功率后，風輪轉速應該保持恒定值。而且，當設計好風力機后，風輪半徑也是固定值。結合式(1)、(2)、(3)可以得出，某工況下，風機的功率主要受風速和變槳角度的影響。因此，建立風速和變槳角度之間的映射關系，是確定前饋控制量的重要環節。本文首先采用牛頓拉夫遜算法得到風速和與之對應的變槳角度，再采用最小二乘法擬合它們之間的非線性映射關系。最小二乘法擬合方式要求目標值和實際值的差的平方和最小[13]:

(20)

得到的風速與槳距角的非線性映射關系:

β(V)=a0+a1V+a2V2+…+anVn

(21)

式中,an為擬合系數。

2.4 粒子群優化PID控制器方法

由于PID控制器結構簡單、易于實現且工作可靠，廣泛應用于工業控制領域。當系統出現偏差后，比例環節立刻產生作用，使控制輸出接近目標值。但是，比例環節并不能完全消除余差，通常和積分環節結合使用。積分環節的作用主要用于消除余差，直到偏差變化到零為止。微分環節具有一定的超前控制能力，可以改善時間滯后影響。PID控制器3個參數的選取是實現精確控制的關鍵環節，因此，本文選擇粒子群理論對參數進行優化。

粒子群算法是一種模擬動物覓食過程的智能算法，它從隨機解出發，通過計算、迭代、更新等步驟，得到個體和全局的最優解。對粒子群算法求解過程做如下描述，假設在一個N維空間中有K個粒子，每個粒子的位移和速度分別為Xi=(xi1,xi2,…,xiN)和Vi=(vi1,vi2,…,viN)，i=1,2,…,K。通過迭代，當第i個粒子到達最佳位置時(用最佳適應度表示粒子的最佳位置)，此時，該粒子即為個體中的最佳粒子；如果全部粒子迭代到目前為止的最佳位置時，則為全局最佳粒子。粒子的位置和速度迭代式為[14]：

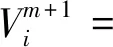
(22)

(23)

式中:m為當前粒子群更新的代數;ω為權重系數;c1為局部學習因子;c2為全局學習因子;r1、r2均為隨機數且∈[0,1]。

3 仿真實驗與結果分析

為了更好地理解所采用的算法，并且讓學生有直觀的認識，選用某型3 MW變槳風力機為例，建立Simulink模型，主要算法在S函數中實現。風力機參數如下：額定功率Pa=3 MW，葉輪半徑R=47.5 m，額定風速V=12 m/s，傳動比k=80，葉輪轉動慣量Jr=6 250 000 kg·m2，電機轉動慣量Jg=15 kg·m2，風輪轉速ωr=2 rad/s。前饋、反饋控制過程中涉及的參數如下：氣動轉矩參數Tψ=0.1，粒子迭代代數m=100，權重系數ω=0.5，局部學習因子c1=2，全局學習因子c2=2，隨機數r1=1，隨機數r2=1，比例系數kp=49.474 6，積分系數ki=50.985 9，微分系數kd=0.206 6。控制系統的穩定性和目標跟蹤是兩個很重要的性能指標，為很好的檢驗這些性能，仿真過程選擇躍變風速為輸入信號。當風速發生躍變時，檢驗控制器在突變信號作用下的穩定性，同時也檢驗跟蹤控制的多項性能指標。仿真過程中發現，粒子群算法中的參數是影響優化速度的重要因素。因此，在滿足控制器精度的基礎上，也要盡可能降低優化時間的消耗，要將粒子群更新代數設置為一個合適的值(見圖2、3)。

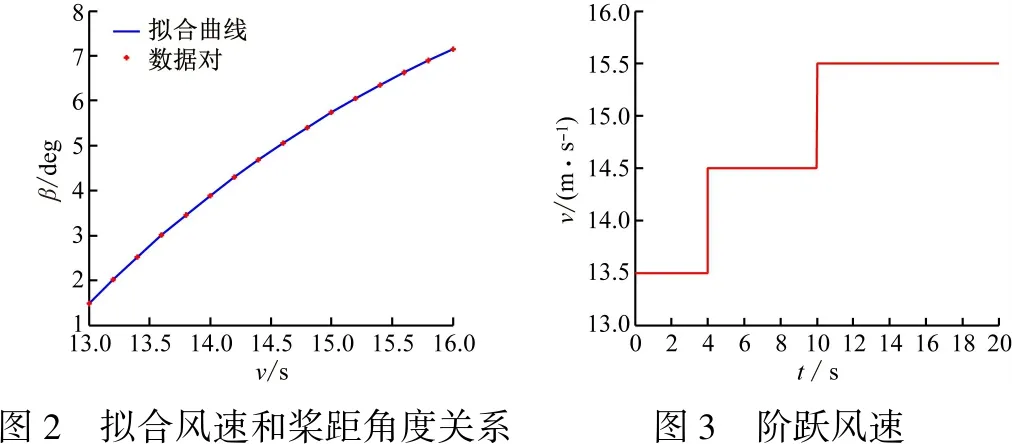
圖2 擬合風速和槳距角度關系圖3 階躍風速

從圖4可以看出，當風速發生躍變時，和常規PID控制器相比，本文采用的復合控制器輸出的變槳角度響應速度快，系統調節時間短，可以很快收斂到穩定值。超過額定風速后，變速風力機的轉速應該保持在額定值，從圖5可以看出，采用常規PID控制器時，轉速的超調量大、調節時間長，并且，在風速穩定時刻，轉速隨著風速增大，與額定轉速存在偏差。轉速偏離額定值，直接導致輸出功率也與控制目標存在差距。對比本文采用的復合控制器，當風速發生躍變時，轉速的超調量小，調節時間短，而且，無論風速怎么增大，轉速始終能夠保持在額定值。因此，系統的動態特性得到改善，輸出功率質量明顯提高(見圖6)。

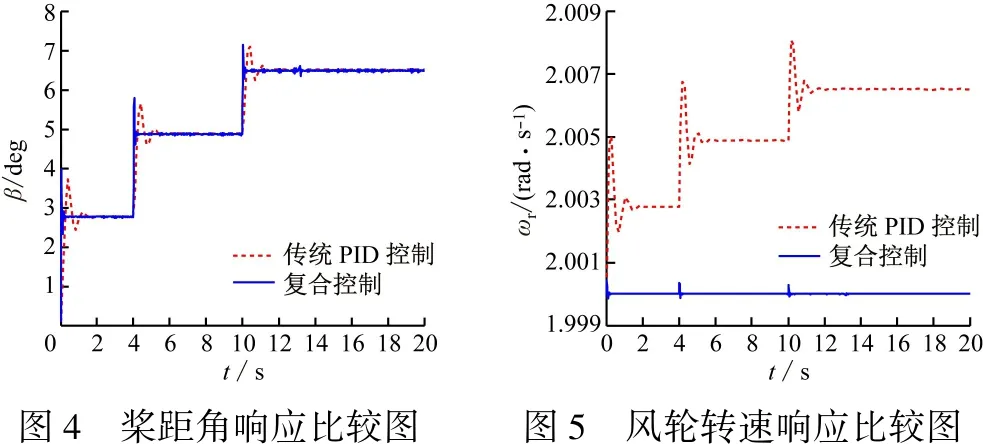
圖4 槳距角響應比較圖圖5 風輪轉速響應比較圖

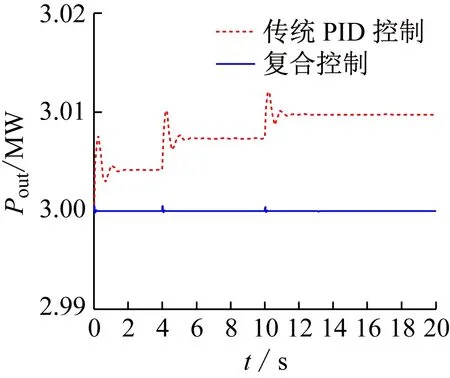
圖6 輸出功率響應比較圖

4 結 語

風力機是一個具有時間滯后的非線性系統，常規PID控制器無法滿足控制系統性能要求，采用將前饋控制和反饋控制相結合的方法，可以有效克服系統的滯后影響，提高系統的穩定性和控制精度。采用Simulink仿真的方式將抽象的理論知識可視化，不僅可以加深對知識的理解，還可以學習到如何將理論知識轉化為實際技術進行應用。這種教學方式可以有效提高教學效果，培養學生的學習興趣，增強學生的動手能力和解決實際問題的能力，是一種行之有效的教學方法。