數學實驗工具的設計與實驗教學
——以“多功能套尺”的設計與實驗教學為例

☉江蘇省睢寧縣高級中學初中部 王翠玲

☉江蘇省泰州市教育局教學研究室 錢德春

數學實驗是學生通過動手、動腦“做”數學的一種學習活動，它以學生為主體，以學具、實物模型或計算機等為工具，以實際操作為行為特征，以探究未知結論、驗證感知結論、幫助理解結論為目的，它是一種以實驗為媒介的數學思維活動.實驗工具是數學實驗的重要載體.筆者在教學實踐中設計了數學實驗工具“多功能套尺”，獲得了2016年江蘇省數學實驗創新大賽一等獎.本文以“多功能套尺”為例，談談初中數學實驗工具設計在數學教學中的應用，以及由此對教與學產生的價值.

一、多功能套尺的設計緣由

邊與角及它們之間的關系是三角形、四邊形主要學習內容.這些知識形成的途徑多樣，一個有效的途徑是學生在教師的引導下，經歷動手操作、觀察、猜想、比較等過程體驗、感悟、理解、掌握和內化.多年的教學實踐，讓筆者不禁思考：能不能制作一種實驗工具，通過操作，更直觀地發現和理解圖形、邊、角及它們之間的關系呢？筆者用學生身邊唾手可得的硬紙板構思、設計了“多功能套尺”.

二、多功能套尺的結構與操作

1.多功能套尺的結構

多功能套尺將刻度尺與量角器融合為一體，是一套自帶刻度的多變工具.

（1）構成：多功能套尺由一把固定標尺、一把固定角尺和若干把滑動角尺組合而成（如圖1）.角尺是量角器和刻度尺的合體，量角器的零刻度線與刻度尺的刻度線重合，量角器的中心與刻度尺的零刻度重合（這是獲得準確的實驗數據的關鍵保障）；每一把角尺都可以靈活拆卸.

（2）分類：根據角尺能否滑動，角尺分為固定角尺（簡稱“定尺”）和滑動角尺（簡稱“動尺”）.

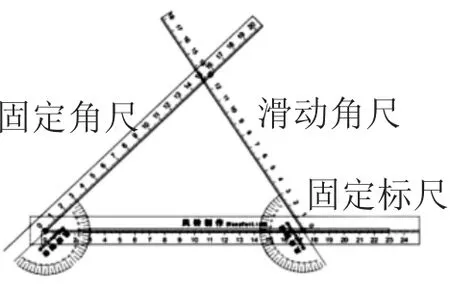
圖1

2.多功能套尺的操作

滑動和旋轉是多功能套尺的主要操作方式.借助多功能套尺旋轉或滑動構造相應模型，探究三角形或四邊形所蘊含的邊或角之間的關系及全等變換、相似變換等.

在定尺的刻度線上有滑槽，動尺可以根據實驗需要在滑槽內滑動，通過滑動動尺，可以改變標尺的示數，以調整圖形邊的大小；同時，每一把角尺都可以通過旋轉，改變其與其他尺子的夾角，從而調整圖形角的大小.

三、多功能套尺的功能與應用

以與三角形有關的教學為例.利用多功能套尺可以進行與一般三角形、等腰三角形、直角三角形、相似三角形或全等三角形等相關知識的實驗探究.根據數學實驗目的的不同，其實驗可以分為三種類型：探究型、驗證型和深化理解型.

1.探究未知結論

實驗1：利用多功能套尺探究三角形全等的條件.

實驗目的：通過實驗，探究兩個三角形全等所需要的條件.

實驗準備：每名學生準備一副多功能套尺.

實驗方式：小組合作（4個或多個學生一組）.

實驗過程：首先，教師提出問題：當兩個三角形具備多少組邊或角相等的條件時，它們就全等呢？

經過學生討論，確定實驗問題：

（1）當兩個三角形的一組邊或角相等時，它們全等嗎？

（2）當兩個三角形的兩組邊或角相等時，它們全等嗎？

（3）當兩個三角形的三組邊或角相等時，它們全等嗎？

（4）當兩個三角形滿足什么條件時，它們全等？

步驟1：以小組為單位，學生甲隨機構造一個三角形（如圖2），以該三角形為“樣本”.

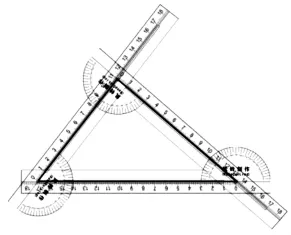
圖2

步驟2：其他學生再構造一個三角形，使所構造的三角形與學生甲構造的三角形的關系分別滿足以上條件，通過套尺上的標尺和量角器的示數，學生觀察、比較其余的各組邊、角是否確定對應相等（或利用“疊合法”），驗證此時兩個三角形是否能夠完全重合，從而判斷兩個三角形是否全等（如圖3）.

步驟3：歸納實驗結論：

（1）當兩個三角形的一組邊或角相等時，它們不一定全等.

（2）當兩個三角形的兩邊及其夾角分別相等時，兩個三角形全等（簡稱為“邊角邊”或“SAS”）.

（3）當兩個三角形的兩邊及其中一邊所對的角分別相等時，兩個三角形不一定全等.

（4）當兩個三角形的兩角及其夾邊分別相等時，兩個三角形全等（簡稱為“角邊角”或“ASA”）.

（5）當兩個三角形的三邊別相等時，兩個三角形全等（簡稱為“邊邊邊”或“SSS”）.

借助多功能套尺進行探究實驗，可以獲得三角形全等的條件：“SAS”“ASA”“SSS”.另外，根據三角形的內角和定理，“ASA”的推論——“AAS”也是成立的，所以不需要實驗探究.

對于“HL”，筆者在實驗中設計以下實驗過程：

（1）觀察圖形，提出問題：當兩個三角形的兩邊及其中一邊所對的角分別相等時，兩個三角形不一定全等，那么，當兩個三角形再滿足什么特殊條件時它們全等？

（2）動手實驗，獲得結論：斜邊和一條直角邊分別相等的兩個直角三角形全等（簡稱“HL”），即相當于增加“其中一組邊所對的角是直角”的條件.

在探究三角形全等條件的實驗中，學生以小組（至少兩人）合作為主要方式，在實驗中思辨、討論、發現與歸納，獲得三角形全等的條件，使“SAS”等“冰冷的美麗”變成“火熱的思考”.

2.驗證感知結論

實驗2：利用多功能套尺驗證“等邊對等角，等角對等邊”.

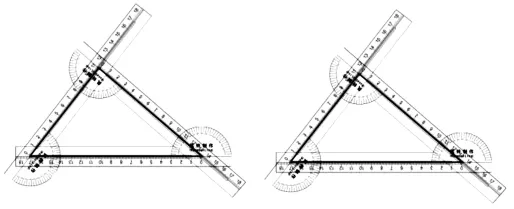
圖3

實驗過程：首先構造一個三角形.通過旋轉圖中的任意兩把動尺，調整三角形角的大小.當三角形中兩個內角相等時（如圖4），學生根據刻度尺上的示數可以發現：相等的兩個內角所對的邊也相等.當然，學生通過旋轉標尺或滑動量角器，可以調整三角形各邊的大小.在三角形的兩條邊相等的條件下，觀察量角器的示數可以發現：在三角形中，相等的兩條邊所對的角也相等.

另外，通過旋轉標尺或滑動量角器調整三角形各邊或角的大小，也可以驗證等邊三角形的性質和判定.

類似地，我們可以利用多功能套尺驗證“大角對大邊，大邊對大角”.

該實驗可以分“兩步走”.

第一步：每一名學生任意構造一個三角形，通過旋尺和量角器的示數獲得三角形各邊、各角的度數.

第二步：學生在明確“對邊”“對角”的前提下，比較每一個角所對的邊的大小關系，可以發現：在三角形中，較大的角所對的邊較大，較小的角所對的邊較小；反之亦成立.

不同的學生往往構造不同的三角形，教師鼓勵同學之間相互交流，從而獲得更為充分的三角形實例，為探究實驗提供更為豐富的實驗資源.

實驗3：探究“由平行線得相似”.

在三角形套尺的基礎上，再安裝一把動尺.下面，通過兩種操作方式進行探究實驗，以探究相似三角形的判定定理：平行于三角形一邊的直線與三角形的另外兩邊相交，所構成的三角形與原三角形相似.

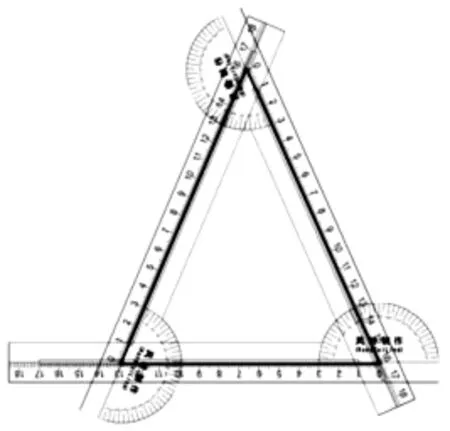
圖4

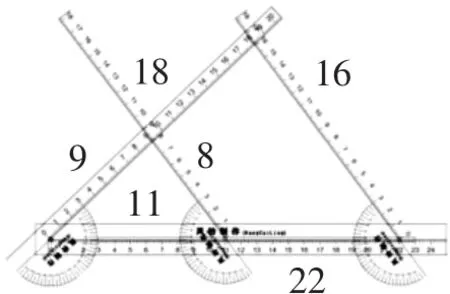
圖5

方式一：“旋轉”.首先旋轉標尺，調整量角器的示數，根據“同位角相等，兩直線平行”，使其中兩把標尺平行.學生根據標尺的示數可以獲得圖中的兩個三角形各邊的長度，如圖5所示，小三角形的各邊分別為8cm、9cm、11cm，大三角形的各邊分別為16cm、18cm、22cm，通過計算可以發現8∶16=9∶18=11∶22=1∶2，即這兩個三角形的各邊對應成比例，從而初步驗證“平行于三角形一邊的直線與三角形的兩邊相交，所構成的三角形與原三角形相似.”

方式二：“滑動”.在保持兩條標尺平行的條件下，滑動角尺改變圖中兩個三角形各邊的長度，通過計算得到兩個三角形的各邊對應成比例，加深學生對“由平行線得相似”的理解.

類似地，根據相似三角形的不同判定條件，學生通過小組合作，借助一般的三角形套尺，可以構造不同的相似三角形模型（如圖6），從而為對應實驗提供充分的數據，加深學生對“三角形相似的條件”的理解.

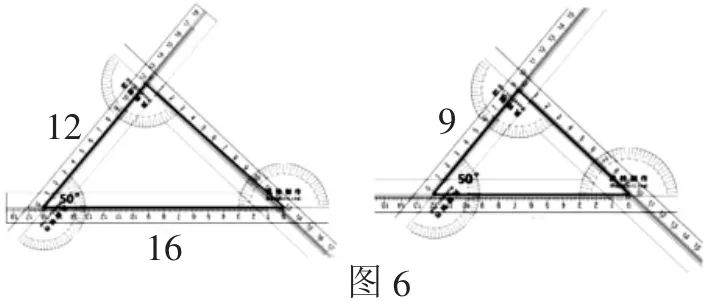
圖6

3.深化理解結論

實驗4：理解銳角三角函數的意義與“增減性”.

首先構造直角三角形.通過旋轉角尺，調整量角器的示數，設置直角三角形中銳角的大小.根據標尺交點的示數能直接獲知直角三角形各邊的長度，學生根據銳角三角函數的概念可以求出對應的銳角三角函數值.

如圖7左圖，該直角三角形的一個銳角為30°，此銳角所對的直角邊為7cm，斜邊為14cm，則sin30°=7∶14=.

在保持30°角不變的情況下，滑動角尺，改變30°的角所在的直角三角形各邊的大小，如圖7右圖，此時，該銳角所對的直角邊為9cm，斜邊為18cm，則sin30°=9∶18=1∶2.也就是說，30°角所對的直角邊與斜邊的比值不變，即30°角的正弦值總等于.類似地，我們可以驗證其對應的其他銳角三角函數值也分別不變.通過以上實驗，我們可以獲得結論：當一個銳角的大小確定時，其對應的銳角三角函數值也隨之確定.

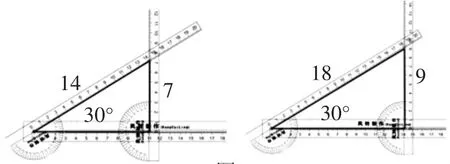
圖7

同時，通過直角三角形套尺（如圖8），學生能充分感知：當一個銳角的大小改變時，其對應的銳角三角函數值隨之改變，從而使學生深刻理解銳角三角函數的意義.

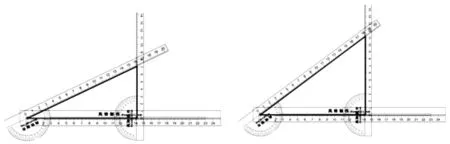
圖8

通過“旋”“滑”“看”“算”，手、眼、腦并用，把操作實驗與探究計算相結合，不僅可以對與三角形相關的一些數學結論進行探究與驗證，還可以對四邊形等多邊形的數學結論進行探究與驗證，如驗證四邊形的不穩定性（如圖9）、探究平行四邊形及特殊平行四邊形的性質與判定（如圖10）、任意正多邊形的性質與判定（如圖11）等，從而深化學生對相應知識的理解.

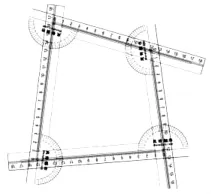
圖9

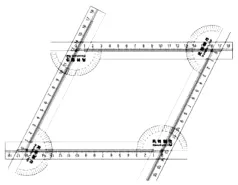
圖10

圖11

四、數學實驗工具設計與運用對教與學的影響

作為學校數學教研組的一項研究項目，從最初的“硬紙板套尺”到目前的多種透明塑料套尺，伴隨著“多功能套尺”不斷改進、優化與完善的過程，學校的數學教師與數學教學發生了可喜的變化.數學教師開發與應用工具進行實驗教學的熱情得到激發，教學理念發生了新的變化，教學方式產生了根本性的變革；學生的學習方式得到了優化、數學學習興趣得到了激發，數學思維能力也得到了顯著的提升.

1.激發了教師實驗教學的熱情

多功能套尺的成功設計與教學的有效應用，帶動了學校數學教研組教師數學實驗教學的熱情，也激發了他們的工具設計與開發的靈感.有的教師制作了木質套尺教具，有的教師制作了其他創新型實驗工具，其中，“多變的四邊形尺”在2018年江蘇數學實驗創新設計大賽中獲得一等獎.

2.更新了教師的數學教學理念

皮亞杰的發生認識論認為，認識的心理發生既不是來自先天的遺傳，也不是來自后天的環境，而是來自主體的行動.數學實驗強調在探究活動中，學生主動參與、自主探究，親身經歷規則、基本事實及推論等的形成過程，強化“做中學”的意識，真正體現了學生的主體地位.

3.變革了教師的數學教學行為

以實驗工具為支撐的數學教學，變傳統的教師“知識講授”“演示實驗”為學生“自主操作”.學生借助工具動手操作、動腦思考，自主探索數學知識，擁有了創新的機會，體驗了數學探究、發現知識的樂趣.

如“實驗2”中，學生通過開放性實驗，借助多功能套尺，不僅可以驗證“等邊對等角，等角對等邊”，還能獲得等邊三角形的三個角都是60°等結論.

4.優化了學生的數學學習方式

數學實驗強調“做”數學的過程，核心思想是以工具為載體，學生手腦并用，內外互動，讓學生親身經歷，以帶給學生深刻的學習體驗和成果.可以說，數學實驗工具恰恰提供了支撐數學學習方式變革的載體，它變結果性知識為過程性知識，變接受性學習為探究性學習.借助多功能套尺等工具進行數學實驗，可以有效地優化學生數學學習的方式.

以“實驗1”為例.在傳統教學中，學生由于沒有經歷“三角形全等的條件”的探究過程，只知其然而不知其所以然，往往死記硬背結論.還有的學生因為缺少實驗工具，一般需要利用直尺、圓規，甚至刻度尺、量角器等多種工具畫圖，然后度量、比較，而且由于工具的限制，難以運用“疊合法”，在驗證滿足一定條件的兩個三角形是否全等時，常常只能通過具體的邊、角的大小來確定，實驗效果不明顯.學生借助多功能套尺進行實驗，可以直觀、高效地探究兩個三角形全等的條件.

5.提升了學生的數學思維能力

數學實驗是一種將操作、觀察、頓悟等融為一體的數學思維活動.學生在教師指導下，經歷操作、觀察、猜想、發現、驗證等數學學習的全過程，有效促進了數學理解，發展了數學思維.

如在“探究平行四邊形及特殊平行四邊形的性質與判定”教學中，學生借助多功能套尺進行“四邊形→平行四邊形→矩形（或菱形）→正方形”的操作實驗，較好地理解條件之間的關聯性和圖形之間的從屬性，增強了數學思維的縝密性.

五、結語

數學實驗工具的設計與開發，促進了教師的專業發展、教學水平的提高；數學實驗工具在教學中的應用，為學生通過動手、動腦“做”數學提供了可能，引領學生真正經歷數學學習的全過程，增強了學生的手腦協調及思維能力.

需要說明的是：數學實驗是一種“做”數學的活動，而“做”數學具有形象、直觀、感性的特點，“證”數學則具有抽象、嚴謹、邏輯的特點，數學教學只有將實驗的“做”數學與推理的“證”數學有機結合，才能使二者優勢互補、相得益彰，真正實現將“脖子以上的學習”發展為全身心融合的學習［1］.