淺談初中數學如何試行“一題一課”的有效復習

☉浙江省蒼南縣龍港十二中 張培懇

復習課是數學課堂的重要課型之一，教師指導學生溫習已經學過的知識，厘清知識來龍去脈，強化知識，加深理解，使知識系統化，再建構知識體系，做到“豎成線、橫成片”，使學生能更加全面地理解、掌握相關知識，提升學生綜合應用知識解決數學與實際問題的能力.基于復習課教學的要求，結合溫州九山中學溫老師的一節課“代數式復習”和教育專家的講座，談自己的幾點想法.

一、低起點，順勢引導，創造良好的課堂學習氛圍.

12月11號上午，觀溫州九山中學溫老師的一節課“代數式復習”.復習之前，溫老師先投影一個簡單的數學式子，如-x2y，并問：“這是我們曾經學過的什么式子？”此時全體學生異口同聲回答：“是一個單項式.”這樣由一個簡單的單項式引入，低起點，吸引全體學生的眼球，幾乎每個學生都能參與回答，營造一個良好的課堂學習氛圍.接著溫老師順勢追問：“你們還能列舉一些其他的單項式嗎？”這時學生紛紛舉手，溫老師隨意點名舉手學生回答問題，并做簡單的板書，如x、3xy、-3、4b2、a2等.接著溫老師把幾個學生講的單項式用不同的數學符號連成新的數學式子，并追問，如：-x2y+x-3是什么式子？學生也容易回答這是曾經學過的多項式，再次讓學生口述單項式和多項式的定義，師生共同梳理了單項式和多項式統稱為整式.繼續追問：“還有有別于整式的式子嗎？”此時學生自然想到還有分式、根式等統稱為代數式.課堂教學自然步步引入這節課所學的內容——代數式復習（板書課題）.這樣的課堂設計，再加上溫老師巧妙運用課堂語言，順勢引導學生回顧所學的知識，系統地整理了知識脈絡，自然形成知識體系，鞏固所學的基礎知識，課堂教學達到良好的效果.

二、巧串問題，綜合訓練，提煉數學思想，整體提升

溫老師前面提到了幾個單項式和多項式，然后讓學生添加自己喜歡的數學加、減符號，自然地過渡到合并同類項，追問什么是同類項及同類項合并的方法，再次追問能否創設稍復雜一些的多項式，這時學生想到幾個帶括號的整式加、減，由此順勢過渡到去括號法則的復習與回顧.為了更深層次地鞏固知識，溫老師要求學生完成老師提供的圍繞一題串聯的數學問題學習單（課前預設），先讓學生自主完成，教師課堂巡視，尋找學生的不同做法及錯誤類型，讓學生相互講評，大大提高了學生的學習積極性，也能更好地查漏補缺，收到更好的學習效果.在簡單梳理好基礎知識點后，溫老師另外投影幾個預設的問題：

（1）設A=3x2y+2xy，B=2x2y+xy-3，C=xy2.求A-2B+C.

（2）若A-2B+D的結果與x的取值無關……

（3）當2x-3y=1時：

①4x-6y=_______；

②9y-6x+2=_______；

問1：針對性練習：溫老師先將前后桌學生4人分為一組，由于課堂上沒有投影儀，溫老師靈活采用小白板，讓學生分組討論，各組代表將答案寫在小白板上，教師巡視尋找典型的錯題分析，如以下錯誤的解答過程：A-2B+C=3x2y+2xy-2（2x2y+xy-3）+xy2=3x2y+2xy-4x2y-2xy+6+xy2=6.這組學生出錯，在于不小心將3x2y、-4x2y、xy2三項都看成同類項合并為0.最后大家一起糾正，給出正確的答案，即原式=-x2y+xy2+6.

通過辨析錯因，澄清學生錯誤的認識，提高學生審題和解題的嚴謹性.

問2：串接上題并追問：“若A-2B+D的結果與x的取值無關……”，這個問題的答案不唯一，是開放性問題，溫老師先讓學生思考，最后有學生舉手回答：

甲：D=x2y，乙：D=x2y+3，丙：D=x2y+常數.

這樣的一題多解，對不同層次的學生都有訓練的作用，有利于培養學生的多種思維能力.但在給出問題（2）時，溫老師沒有做好自然的過渡追問，而是直接給出問題讓學生思考，好多學生沒見過這類問題，不知道如何下手解答，浪費了一些課堂時間.我的想法是：分步給出問題，順勢追問，先說問題（1），學生完成得很棒，再追問：“若將問題（1）中的A-2B+C變為A-2B+D”，同時投影給出問題（2），并問這個D將是一個什么代數式，這樣做，將有利于學生從代數式方向思考，尋找正確的答案，可以節省點時間，完成一題多解，培養學生從多角度思考問題的良好品質.

問3：綜合性練習：當2x-3y時，

①4x-6y=______；

②9y-6x+2=_____；

溫老師推出這個問題時，先讓學生獨立思考，看哪名學生可以最快回答.這樣的設問，引起許多學生積極投入認真思考，很快有幾名學生舉手回答：

甲說4x-6y=2，溫老師追問怎么思考的，甲說4x-6y=2（2x-3y）=2×1=2，運用了整體思想，大家給予肯定，并給予表揚.

接著乙說9y-6x+2=5，溫老師將其歸類為同類題型，只不過問題②解答起來稍微復雜一點兒.

完成了三個小題，溫老師歸納這類題的解題方法，主要是通過簡單變形，運用數學重要解題思想——整體代入思想來解題.對于問題③的設計，我有自己的思考，問題①和②是同一類型題，兩題難度相差不大，可以刪去②，留下時間可以追問問題③是否還有其他解法.由于此類問題是填空題，我們可以采用方法2——特殊值法，由已知2x-3y=1，不妨設x=2，y=1，代入原式成立，同樣可以算出①和③的答案，解題速度快.也可以采用方法3——將原代數式轉化代入求解.可將2x-3y=1轉化為2x=3y+1，代入求得①和③的值，順利過渡到轉化思想的應用.這樣通過一題多解的思考與分析，可以提煉多種解題思想，提高學生的解題技能和思維的寬度，達到更好的復習效果.

三、高落點，結合實踐，學以致用，拓展訓練，提升學習興趣

溫老師在最后順勢過渡到兩個生活中的數學問題：

用：某公園停車場地面的植草磚的設計如圖1所示.已知正方形ABCD的邊長為2b，點E、F、G、H分別是正方形四條邊的中點，圖中陰影部分為植草區域.

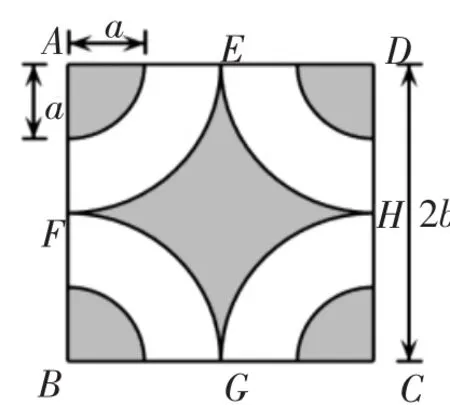
圖1

（1）正方形ABCD的面積為___________；

（2）用代數式表示圖中陰影部分的面積；（結果保留π的形式）

（3）當a=1、b=4時，求陰影部分的面積.

本題第（1）問比較簡單，學生很快口答；對于第（2）問，溫老師先讓學生思考并回答，老師協助，并借助媒體，將學生的思考結果做動畫解釋，學生想到四個角落的小扇形可以拼成一個圓，老師用幾何畫板將原圖中的四個小扇形移出拼成一個半徑為a的圓；原圖挖去四個小扇形后，中間空白的四個扇形剛好也能構成一個半徑為b的圓，再次通過幾何畫板分塊動畫演示，這樣操作直觀、易懂.大多數學生能求出中間陰影部分的面積是一個邊長為2b的正方形減去一個半徑為b的空白圓再加上一個半徑為a的小圓，師生共同得到陰影部分面積為4b2-b2+a2，同時提煉了分割法解三角形面積問題.這樣設計，把簡單的整式應用于生活實際問題中，達到了學以致用，提高學生的學習興趣.

拓：用正方形硬紙板做三棱柱盒子，每個盒子由3個矩形側面和2個正三角形底面組成（如圖2），硬紙板以如圖3所示的兩種方式裁剪（裁剪后邊角料均不再利用）.

圖2

A方法：剪6個側面；B方法：剪4個側面和5個底面.現有19張硬紙板，裁剪時x張用A方法，其余用B方法.

（1）用含x的代數式表示底面的個數為__________，側面的個數為__________.

（2）若裁剪出的側面和底面恰好全部用完，問：能做多少個盒子？

圖3

這樣的實踐性練習，可進一步提高代數式的應用，為今后學習三棱柱的知識做好鋪墊，也讓學生知道今天的學習為今后更深層次的學習服務.由于時間關系，溫老師沒有時間給出本題的解答，只是簡單分析了一下，幾句話帶過，后面就總結歸納這節課所學、所思、所得，結束這節課.我覺得這樣結束有點兒草率.最后雖然沒時間，但應給出本題的答案，并要求學生對照答案，作為本節課的作業，思考驗證本題的答案.若本題不會解，或有疑問，再與老師交流，這個收尾留有余聲更好.

綜上所述，一節有效的數學復習課，并非單純的數學知識重述，而應是知識點的整合、深化、升華.樂清市教研室特級教師吳立建老師的一句話“課堂教學倡導一題一課，題量少，講究深挖”，上課前做到“讀懂學生，讀懂題目，讀懂教學”.溫老師這節課從一題開始，順勢設問，層層遞進，挖掘知識，在課堂生成中靈活串題，預設問題厘清知識脈絡，學以致用和拓展訓練提高學習興趣，確實有效.我個人有幾點想法：（1）在倡導一題一課時，老師在課堂上的設問和追問語言要精練，過渡自然，偶爾帶點兒幽默；（2）隨機應變，順勢引導課堂的生成，善于將生成的問題妥善歸類并提煉核心問題的講解，確保落實重、難點；（3）不斷加強學習，提高數學解題能力和靈活駕馭課堂教學的能力；（4）上課前要精心設計和準備，隨時準備解答偶發的疑難問題；（5）同伴的合作、專家的引領，把握每節復習課的特點，選擇好策略，巧妙應用媒體.只要認真對待，不斷學習與創新，始終注意激發學生的學習興趣，定會有驚喜的復習效果.F