圍繞“主問題”　感悟數學本質

謝玥

【摘要】本文以蘇教版數學三年級下冊“小數的初步認識”的教學實踐為例，圍繞主問題：任意兩個相鄰的整數之間會有新的數存在嗎？從O～】以內的一位小數的探索，形成整體進入的牽引力;任意兩個相鄰的整數內一位小數的研究，形成認知結構的支撐力;生活中小數意義的發掘，形成課堂活動的凝聚力;關注發展，形成后續學習的推動力，這幾個方面引領學生層層深入地探究，感悟數學本質。

【關鍵詞】主問題 數學教學 牽引力 支撐力 凝聚力

“小數的意義”在蘇教版教材的編排中安排在兩個年級學習，三年級下冊“小數的初步認識”和五年級上冊“小數的意義”。在教學三年級下冊第六單元“小數的初步認識”的前期，學生儲備的知識基礎有：（l）掌握了整數的認識知識結構。（2）已經接觸了分數的初步認識。從整數到小數，是數域的一次擴展，學生的數概念從具有離散性的整數向具有稠密性的（非負）有理數發展。在學習整數的認識和分數的初步認識過程中，學生經歷了從具體到半抽象的過程，對抽象的數字符號所表示的具體意義也有了一定的認識。所以，本課設計在數軸上把相鄰的兩個整數之間的距離平均細分并用小數表示的過程，讓學生在經歷小數形成的過程中了解小數與整數、小數與分數的內在關系。初步感悟小數的一些基本概念，小數的表示、十進制的計數單位、小數的精確作用，以及小數與數軸上點的對應關系等。為使知識系統化.本課以“主問題”為線索，圍繞“主問題”，引領學生進行層層深入的數學研究。

一、情境激趣，生成主問題

出示情境：這兩個同學身高分別是多少？比一比。學生大多數認為一樣高。

小結：大多數同學認為他們的身高一樣高，真的一樣高嗎？通過今滅的研究，我們可以進·步比出他們的高矮。

師：（估算）026÷4，43÷5。

生：第一題商是6余2，第二題商8余3。

師：（提出主問題）6～7之間、8～9之間還會有數存在嗎？這樣的任意兩個相鄰的整數之間會有新的數存在嗎？

[思考]數學教學中的“主問題”，是引導學乍對教學內容進行研究的重要問題、中心問題或關鍵問題。這樣的任意兩個相鄰的整數之間會有新的數存在嗎？這個問題是在學生通過比身高和計算的過程中，發現所學知識不夠表達，急需獲得新知的需求狀態而進入數學學習過程的。“主問題”既是對傳統的課堂提問方式的改造和創新，也是對數學課堂活動方式的改造和創新。用“主問題”來形成課堂教學步驟的課，往往表現出一種“線索”之美，表現出“妙在這一間”的新穎創意。

二、圍繞主問題，引領學生遞進性探究

探究一：O-I以內一位小數的探索，形成整體進入的牽引力

第一層次：0～1米的一位小數。

師：首先從兩個整數入手。選擇最小的研究起。0～l之間有新的數存在嗎？

師邊說邊畫：把1米長的線段，平均分成10份，l份是多少呢？你能表示出來嗎？

生1：1份表示1分米。

生2：1份也可以表示10厘米。

師：1分米、10厘米。還是用整數表示的，但是單位變了。如果不改變單位怎么表示？

師：是l米的1/10，就是1/10米。

還可以表示為0.1米。0.1米也表示把l米平均分成10份，表示這樣的l份。介紹小數點，0.1的讀法寫法。

讓學生說一說。如果取其中的2份，用分數怎么寫，小數怎么寫，又是什么意思呢？0.2米里面有幾個0.1米？

學生相互說一說，然后在作業紙上把2分米改寫成分數和小數。

2分米是1米的2/10，也就2/10米，還可以寫成小數是（0.2）米。

取其中的三份呢？四份呢……用和它原來單位一樣的分數、小數來表示。學生相互交流。

板書：1米的1/10，就是1/10米，還可以表示為0.1米。

第二層次：從1米平均分成10份，遷移到其他計量單位。

師：這條線段只可以表示1米平均分成10份嗎？你可以把什么單位平均分成IO份？那么，每一份用同樣的單位，分數、小數又是怎樣表示呢？

生3：把進率為10的平均分，比如1分米、1厘米平均分成10份。

師：除了長度單位還有其他單位嗎？

生4：“1元”平均分。

學生在作業紙上完成：這條線段還可以表示什么量？在1后面寫上合適的單位。在數點上面寫分數和下面寫對應的小數。

資源生成：學生把進率為10的平均分，比如：1分米、1厘米、1元。也會有學生把進率不是10的平均分成10份，比如：1千克。

第三層次：聚類O～1之間的一位小數。

實物投影上把學生的作業紙放在一起。請同學仔細觀察，這里除了單位不一樣、長度不一樣外，有什么相同的地方？

學生觀察交流。

生l：分數、小數相同。

生2：都把1個量平均分成了10份。

生3：上面都是十分之幾，下面都是零點幾。

老師把大家找到的相同的地方在PPT呈現出來，大家可以更清楚地觀察分數與小數之間有什么關系。

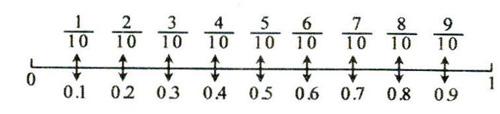
小結：都是把0～l看作一個整體，平均分成10份，十分之幾就是零點幾。

板書：像這樣的0.1、0.2、0.3......它們小數點的右邊只有一位，我們叫作一位小數。一位小數表示十分之幾。邊放PPT：縮短O～l，問：O～l之間有多少個一位小數？介紹0.1就是計數單位。0.9里面有幾個0.1？ 10個0.1是多少？

同桌互說。認識計數單位就是0.1，感知一位小數的組成。

板書：10個0.1是1。

[思考]小數來自哪里，老師在這里及時引領了探究路徑，把—個單位平均分成10份，十分之幾就是零點幾，讓學生沿著研究路徑從許多具體的單位l找到分數與小數間的對應關系，再通過尋找相同點的方法，從具象中歸納出抽象的知識內容。從知識內容的層面考慮，本片段：O～l以內一位小數的形成過程，在這里架構了整數分數小數知識之間的聯系，這個板塊的設計不僅僅停留在學生小數的來源的層面，更在于豐富學生的探究體驗。在體驗與感悟中獲得的知識不是浮在表面的，是有生命力的，最易遷移，能為培養創新意識和實踐能力提供有力的保障。

探究二：任意兩個相鄰的整數內一位小數的研究，形成認知結構的支撐力

第一層次：1～2之間的一位小數的形成。

過渡：

1.只有O～l之間有這樣的一位小數嗎？你能把l～2之間也這樣平均分一分并寫一寫它們之間的小數嗎？

教師呈現作業紙資源：

生1：0.1。

生2：1.1。

交流哪一種寫法對？為什么？

生3：1.1對，1.1里面有1 1個0.1。

生4：1再加上1個0.1，合起來就是1.1。

生5：1～2之間，必須比1大，比2小。

老師表揚同學們的思維正確全面，并讓學生繼續寫出1～2之間的所有一位小數。

師（引導）：1.1如果加上單位米，Il個0.1米，它就表示l.1米。如果加上分米呢就表示什么？你指一個一點幾的小數加上單位，問同桌就是表示什么？同桌互相交流說一說。

師：1.9里面有幾個0.1 ？再加1個0.1呢？

生：1.9里面有19個0.1。再加上1個0.1.就是20個0.1，20個0.1就是2。

第二層次：任意兩個整數之間的一位小數

師：2～3之間會有哪些一位小數？3～4呢？剛才除法估算說商在6～7之間，商在8～9之間，可能會是什么數呢？左右同學互選一個說給同桌聽。1ooo～1001之間有這樣的一位小數嗎？說得完嗎？

學生之間相互交流。

師：同學們說也說不完，我們用一個箭頭來表示還有很多很多。這樣的一條數線就是：數軸。數軸上每個相應的細點，都有一個數存在，無限多。PPT演示數軸的產生：

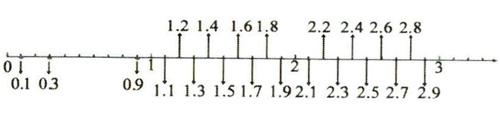
師：剛才講了很多一位小數，那每相鄰的兩個整數之間有幾個一位小數？

生：每相鄰兩個整數之間有9個一位小數。

板書：把黑板上的數線完成生成數軸。

[思考]只有O～l之間有這樣的一位小數嗎？你能把1～2之間也這樣平均分一分并寫一寫它們之間的小數嗎？這是教師創沒的吏有意義的問題情境，讓學生運用上一層次的研究方法來突破教學點，給學生更多的實踐和思考空間，1～2之間的第1小格是寫1.1還是0.1呢？學生在學習小數時的潛藏問題，通過學生之問的探究和碰撞而解決，學生在思辨中明理而不是老師乏味地告知。同樣，這個片段的第二層次，通過一連串到位的設問點撥，引起學生的深層思考后巧妙地提出：說得完嗎？由說也說不完產生了怎樣表達的學習需求，數軸自然而然地生成。在這樣的實踐活動和思維活動中，學生不斷經歷、體驗和探索，在理解和掌握知識技能的同時，獲得了精神層次的享受，是本課最出彩之處。

探究三：生活中小數意義的挖掘，形成課堂活動的凝聚力

第一層次：感受小數的精確性。

課前兩個同學的身高都是132厘米多一些，學劍現在有沒有好辦法讓大家準確知道他們的身高是多少？在學生發言的基礎上電腦演示。132厘米到133厘米之間平均分成10份。

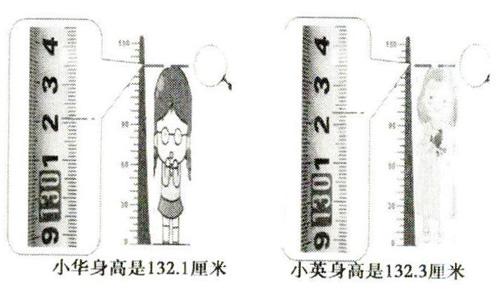
讀一讀兩個同學的身高，并比一比。

小結：和原來的大約132厘米比較，顯得精確了。

第二層次：讀讀說說生活中的小數表示什么意思。

PPT演示生活中的小數（圖略）。在生活中你見到過這樣的小數嗎？說說什么意思.并觀察小數部分不同點。

生：39.4千克比39千克重一些，比40千克輕一些。

小結：一位小數的意義。幫助學生歸納一下讀法。整數部分按以前的讀法讀，小數部分讀數位上的數字。

板書：各部分名稱及書寫法。

第三層次：看圖填上合適的分數或小數

哪幅圖可以表示0.3？

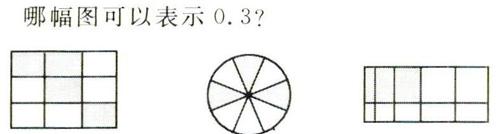
[思考]學生的數學學習不應是單純的知識傳授，它源于生活、富于生活、用了生活。越貼近學生生活的內容越容易引起學生共鳴。通過比身高這個熟悉的生活情境及復習了一位小數的認讀又感悟了小數的精確性。在認讀有小數的許多生活場景的過程中，體會小數在現實生活中的意義，并且發現除了一位小數，現實生活中還碰到過兩位小數，等等。本環節學生經歷了從理性到生活化的應用，再問到理性的思考。學生們積極投入到學習中，對原本已有的直接經驗在頭腦中進行了理性加工，獲得了數學發展和處理問題的能力。

探究四：關注發展，形成后續學習的推動力

今天我們學習了一位小數，知道一位小數的產生、意義及讀寫方法。剛才同學們在讀小數的時候，就知道還有兩位小數，它又是怎樣產生的呢？還有三位小數呢？想一想，回顧一位小數研究的過程，方法能不能用到兩位小數的研究上？

[思考]克萊因認為：“數學是人類最高的智力成就，也是人類心靈最獨特的創作。”我們教給學生知識的同時，也應使用相應的知識去讓學生感受數學的文化魅力，得到精神上的熏陶。整節課，學生在“主問題”的引領下，運用了遷移、類推、抽象等方法，建立了小數的產生及其意義的模型。濃濃的數學味，沒有使學生感到小數概念學習的枯燥，反而隨著整節課的層層推進興趣盎然。這里雖然用寥寥幾句話總結了全課，但是通過回顧學習的方法結構，為后續知識的拓展埋下了伏筆。

【參考文獻】

[1]章晨，小學數學課堂主問題式的教學探索[J].小學科學（教師版），2014（7）.

[2]郁興林.以數學問題的解決為主線，巧妙推進循環教學[J].陜西教育（理論版）.2016（12）.

[3]姜紀華.以問題為主線的數學思維教學[J].數學大世界（下旬）.2017（2）.

[4]漆英，“問題”是數學的“主線”[J].四川教育，2017（12）.